精品解析：广东省江门市新会第一中学等2023-2024学年高一下学期5月联考数学试题

展开

这是一份精品解析：广东省江门市新会第一中学等2023-2024学年高一下学期5月联考数学试题，文件包含精品解析广东省江门市新会第一中学等2023-2024学年高一下学期5月联考数学试题原卷版docx、精品解析广东省江门市新会第一中学等2023-2024学年高一下学期5月联考数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页，欢迎下载使用。

注意事项
1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.
2.选择题每小题选出答案后，用 2B 铅笔把答题卷上对应题目的答案标号涂黑.
3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上.
4.考生必须保持答题卡的整洁，考试结束后，将答题卷收回.
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知（为虚数单位），则（）
A. B. C. D.
2. 在中，已知，，，则（）
A. B. C. D.
3. 下列说法不正确的是（）
A. 正棱锥的底面是正多边形，侧面都是等腰三角形
B. 棱台各侧棱延长线必交于一点
C. 用一个平面去截棱锥，底面与截面之间的部分是棱台
D. 棱柱的侧棱都相等，侧面都是平行四边形
4. 为了得到函数的图象，只要把函数图象上所有的点（）
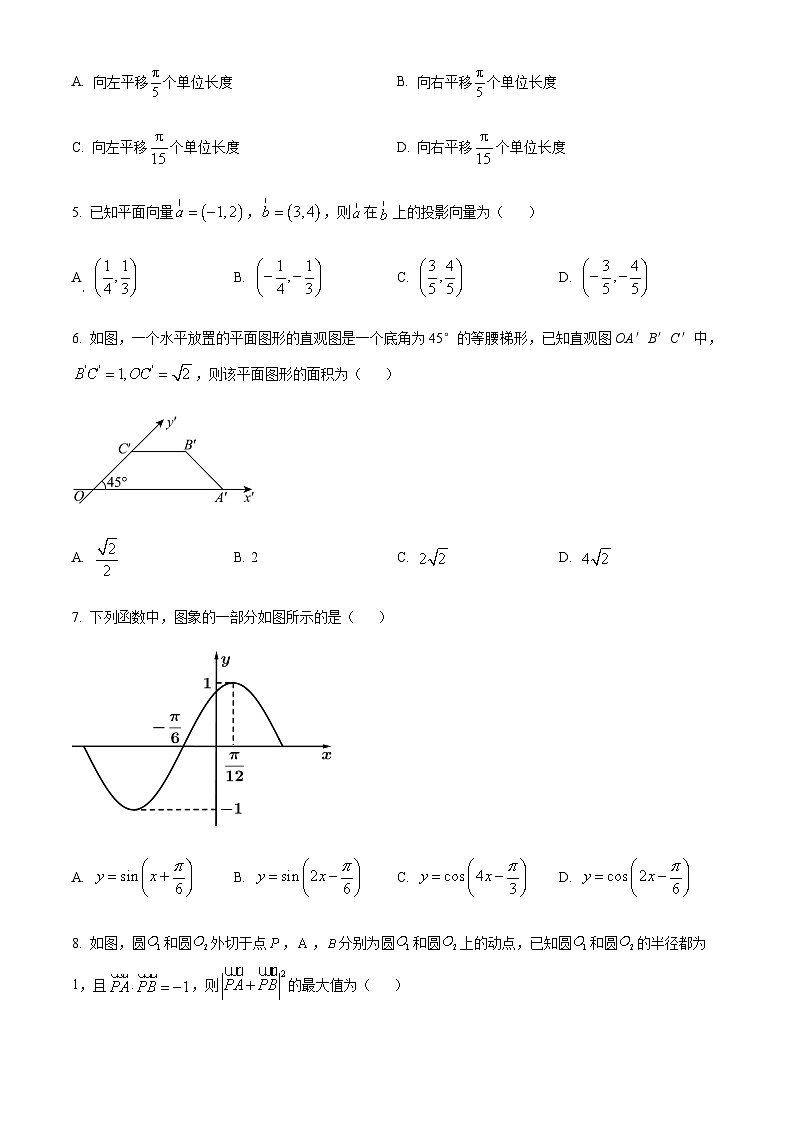
A. 向左平移个单位长度B. 向右平移个单位长度
C. 向左平移个单位长度D. 向右平移个单位长度
5. 已知平面向量，，则在上的投影向量为（）
A B. C. D.
6. 如图，一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形，已知直观图OA′B′C′中，，则该平面图形的面积为（）

A. B. 2C. D.
7. 下列函数中，图象的一部分如图所示的是（）
A. B. C. D.
8. 如图，圆和圆外切于点，，分别为圆和圆上的动点，已知圆和圆的半径都为1，且，则的最大值为（）
A. 2B. 4C. D.
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 设为虚数单位，下列关于复数的命题正确的有（）
A. B. 若互为共轭复数，则
C. 若，则D. 若复数为纯虚数，则
10. 下列命题中正确的是（）
A. 用与球心距离为1的平面去截球，所得截面圆的面积为，则球的表面积为
B. 圆柱形容器底半径为，两直径为的玻璃球都浸没在容器的水中，若取出这两个小球，则容器内水面下降的高度为
C. 正四棱台的上下底面边长分别为2，4，侧棱长为2，其体积为
D. 已知圆锥的母线长为10，侧面展开图的圆心角为，则该圆锥的体积为
11. 在三角形所在平面内，点满足，其中，，，，则下列说法正确的是（）
A. 当时，直线一定经过三角形的重心
B. 当时，直线一定经过三角形的外心
C. 当时，直线一定经过三角形的垂心
D. 当时，直线一定经过三角形的内心
三、填空题：本题共3小题，每小题5分，共15分.
12. 已知向量，若，则_________．
13. 已知圆台高为，上底面半径为，下底面半径为，则该圆台的体积为______．
14. 一般地，对任意角，在平面直角坐标系中，设终边上异于原点的任意一点P的坐标为，它与原点的距离是．我们规定：比值，，分别叫做角的余切、余割、正割，分别记作，，，即，，，把，，分别叫做余切函数、余割函数、正割函数.
（1）已知，则的最大值为_______；
（2）设，则的最小值为________．
四、解答题: 本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知向量，．
（1）若，求;
（2）若向量，，求与的夹角的余弦值．
16. 如图所示，在三棱柱中，过BC的平面与上底面交于GH（GH与不重合）.
（1）求证：；
（2）若E，F，G分别是AB，AC，的中点，求证：平面平面BCHG.
17. 设函数.
（1）求的值；
（2）求函数的最小正周期；
（3）求函数在上的最大值.
18. 如图，在中，内角A、B、C的对边分别为a、b、c已知，且为边上的中线，为的角平分线．
（1）求线段的长；
（2）求的面积．
19. 正等角中心（psitive isgnal centre）亦称费马点，是三角形巧合点之一．“费马点”是由十七世纪法国数学家费马提出并征解的一个问题．该问题是：“在一个三角形内求作一点，使其与此三角形的三个顶点的距离之和最小．”意大利数学家托里拆利给出了解答，当的三个内角均小于时，使得的点即为费马点；当有一个内角大于或等于时，最大内角的顶点为费马点．试用以上知识解决下面问题：已知的内角所对的边分别为，
（1）若，
①求；
②若，设点为的费马点，求；
（2）若，设点为的费马点，，求实数的最小值．