山东省滨州市阳信县2024届九年级下学期中考一模数学试卷(含答案)

这是一份山东省滨州市阳信县2024届九年级下学期中考一模数学试卷(含答案)，共16页。试卷主要包含了答卷前,考生务必用0，第II卷必须用0，例如等内容，欢迎下载使用。

温馨提示:
1.本试卷分第I卷和第II卷两部分,共7页。满分为120分。考试用时120分钟。考试结束后,只上交答题卡。
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的学校、班级、姓名、准考证号、考场、座号填写在答题卡规定的位置上,并用2B铅笔填涂相应位置。
3.第卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第I卷（选择题）
一、选择题:本题共8小题,每小题3分,共24分.每小题只有一个选项符合题目要求.
1.水滴穿石,水珠不断滴在一块石头上,经过若干年,石头上形成了一个深为的小洞,则数字0.000000068用科学记数法可表示为( )
A.B.C.D.
2.剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.如图所示的剪纸图形中,是中心对称图形的有( )
A.①②③B.①②④C.①③④D.②③④
3.将含有角的三角板和直尺按如图方式叠放在一起,若,则度数( )
A.B.C.D.
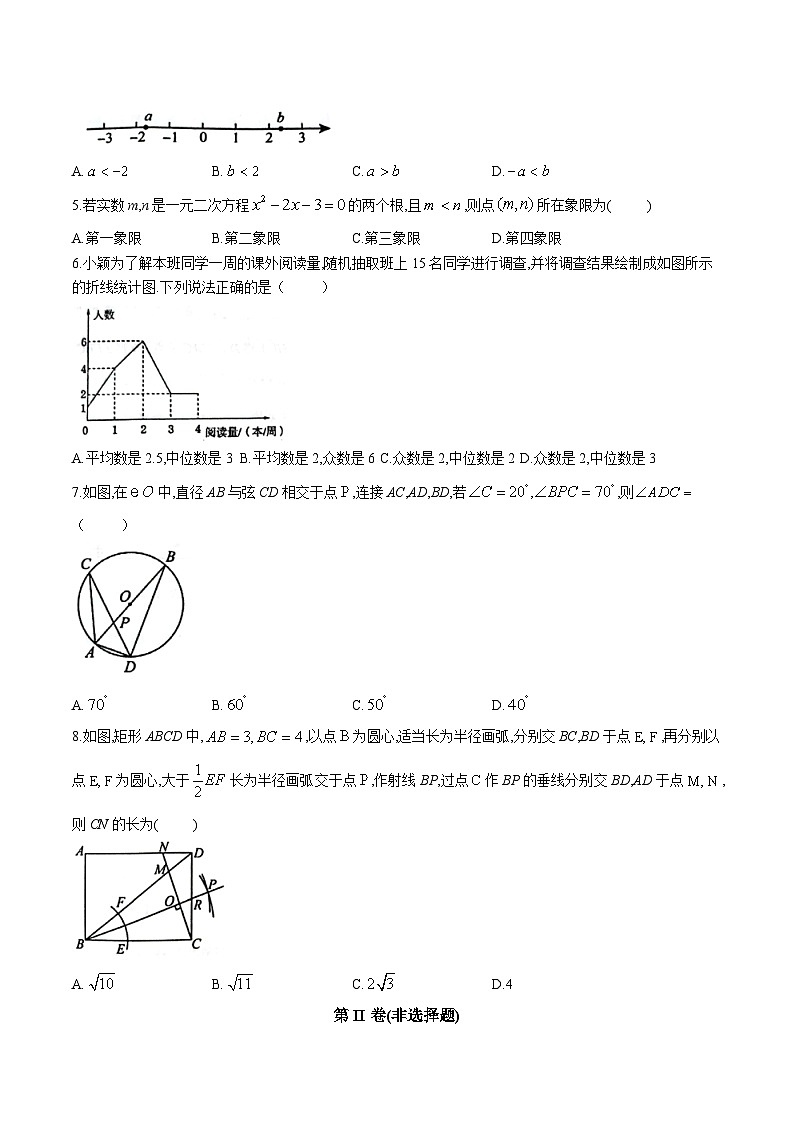
4.实数a、b在数轴上的对应点的位置如图所示,下列结论正确的是( )
A.B.C.D.
5.若实数m,n是一元二次方程的两个根,且,则点所在象限为( )
A.第一象限B.第二象限C.第三象限D.第四象限
6.小颖为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成如图所示的折线统计图.下列说法正确的是（ ）
A.平均数是2.5,中位数是3B.平均数是2,众数是6C.众数是2,中位数是2D.众数是2,中位数是3
7.如图,在中,直径AB与弦CD相交于点,连接AC,AD,BD,若,则（ ）
A.B.C.D.
8.如图,矩形ABCD中,,以点为圆心,适当长为半径画弧,分别交BC,BD于点,再分别以点为圆心,大于长为半径画弧交于点,作射线BP,过点作BP的垂线分别交BD,AD于点,则CN的长为( )
A.B.C.D.4
第II卷(非选择题)
二、填空题:本题共8小题,每小题3分,共24分.
9.要使分式有意义,的取值应满足________________.
10.分解因式________________.
11.分式方程的解是________________.
12.若点都在反比例函数的图象上,则_____________(填“＜”、“＞”或“=”).
13.如图,在中,,线段AB的垂直平分线交AB于点,交AC于点,则________________.
14.《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:
“今有圆材,埋在壁中,不知大小.以锯锯之、深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,AB是的直径,弦于点寸,寸,则直径AB长为________________寸.
15.综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面CD的中点处竖直上升30米到达处,测得博雅楼顶部的俯角为,尚美楼顶部的俯角为,已知博雅楼高度CE为15米,则尚美楼高度DF为________________米.(结果保留根号)
16.已知二次函数的图象与轴的一个交点坐标为,对称轴为直线,下列论中:①;②若点均在该二次函数图象上,则;③若为任意实数,则;④方程的两实数根为,且,则.正确结论的序号为________________.
三、解答题:本题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(本题10分)(1)计算:.
(2)解不等式组:,并写出它的所有整数解.
18.(本题8分)先化简,再求值:,然后从1,2,3,4中选择一个合适的数代入求值.
19.(本题8分)打造书香文化，培养阅读习惯，我县某中学计划在各班建图书角，开展“我最喜欢阅读的书篇”为主题的调查活动，学生根据自己的爱好选择一类书籍（A:科技类,文学类,政史类,艺术类,:其他类）.张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
根据图中信息,请回答下列问题;
(1)条形图中的____________,____________,文学类书籍对应扇形圆心角等于____________度;
(2)若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;
(3)甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
20.(本题10分)如图1,在Rt中,,且BC边上有一点.
(1)请在图1中用无刻度的直尺和圆规作图(不写作法,保留作图痕迹);
①作的角平分线CE,交边AB点;
②作Rt，其中,点在AC边上；
(2)在(1)的条件下，若BC=3,AC=6,点在BC边上运动,则Rt面积的最小值为____________.
21.(本题8分)如图,一次函数的图象与函数的图象交于点和点.
(1)求的值;
(2)若,根据图象直接写出当时的取值范围;
(3)点在线段AB上,过点作轴的垂线,交函数的图象于点,若的面积为1,求点的坐标.
22.(本题8分)如图,AB是的直径,点是上的一点(点不与点重合),连接AC、BC,点是AB上的一点,交CD的延长线于点,且.
(1)求证:BE是的切线;
(2)若的半径为,则BE的长为__________.
23.(本题10分)加强劳动教育,落实五育并举.我县某中学在政府的支持下,建成了一处劳动实践基地.2024年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本(单位：元)与其种植面积(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元.
（1）当__________时,元;
（2）设2024年甲乙两种蔬菜总种植成本为元,如何分配两种蔬菜的种植面积,使最小?
（3）学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降,乙种蔬菜种植成本平均每年下降,当为何值时,2026年的总种植成本为28920元?
24.(本题10分)某数学兴趣小组运用《几何画板》软件探究型抛物线图象.发现:如图1所示,该类型图象上任意一点到定点的距离PF,始终等于它到定直线的距离PN（该结论不需要证明）.他们称：定点F为图象的焦点,定直线为图象的准线,叫做抛物线的准线方程.准线与轴的交点为.其中原点为FH的中点,.例如,抛物线,其焦点坐标为,准线方程为,其中.
【基础训练】
(1)请分别直接写出抛物线的焦点坐标和准线的方程:__________,__________；
【技能训练】
(2)如图2,已知抛物线上一点到焦点的距离是它到轴距离的3倍,求点的坐标;
【能力提升】
(3)如图3,已知抛物线的焦点为,准线方程为.直线交轴于点,抛物线上动点到轴的距离为,到直线的距离为,请直接写出的最小值;
【拓展延伸】
该兴趣小组继续探究还发现:若将抛物线平移至.抛物线内有一定点,直线过点且与轴平行.当动点在该抛物线上运动时,点到直线的距离始终等于点到点的距离(该结论不需要证明).例如:抛物线上的动点到点的距离等于点到直线的距离.
请阅读上面的材料,探究下题:
(4)如图4,点是第二象限内一定点,点是抛物线上一动点,当取最小值时,请求出的面积.
数学试题答案
一、选择题(共8小题，每题3分，共24分.每小题只有一个选项符合题目要求)
1. B 2. A 3．C 4．D 5．B 6．C 7. D 8. A
二、填空题（共8小题，每题3分，共24分）
9． 10． 11． 12．> 13． 14．26 15.．16. ①③④
三、解答题:本大题有8小题（17题10分，18题8分，19题8分，20题10分，21题8分，22题8分，23题10分，24题每题10分，共72分）.解答应写出文字说明、证明过程或演算步骤.
17．（本题10分）
解：（1）
． —————————————————————5分
（2）解不等式①，得，
解不等式②，得， —————————————————————2分
在同一条数轴上表示不等式①②的解集，
原不等式组的解集是， ————————————————————4分
∴整数解为0，1，2． ————————————————————5分
（本题8分）
解：
———————————————————6分
∴当时，原式. ———————————————————8分
19.（本题8分）解：（1）参与调查的总人数为：（人），
，
，
文学类书籍对应扇形圆心角，
故答案为：18，6，； —————————————————3分
（2）（人），
因此估计最喜欢阅读政史类书籍的学生人数为480人； —————————————————5分
（3）画树状图如下：
——————————————————7分
由图可知，共有9种等可能的情况，其中甲乙两位同学选择相同类别书籍的情况有2种，
因此甲乙两位同学选择相同类别书籍的概率为：． ——————————————————8分
20.（本题10分）
解：（1）①如图所示，就是所求； ——————————————————2分
②如图所示，就是所求．
———————————————————5分
（2）∵
∴当时，值最小，此时，
∴四边形为矩形，
∴，
∴，
∴值最小，
∴此时，面积，如图，
∵平分，
∴，
设，
∵
∴
即
解得：，
∴
∴面积的最小值为：．————————————————————10分
21（本题8分）解：（1）将点代入一次函数，
，
故，
将代入反比例函数，
得； —————————————————————2分
（2）由（1）得，
联立一次函数和反比例函数，得
，
解得，
故，
由图像可知，的取值范围为；—————————————————5分
（3）设，且，交x轴于点M，如图；
，
，
，
解得，
点P的坐标为或．
—————————————————————8分
22．（本题8分）
（1）证明：是的直径，
，
，
，
，
，
，
，
，
，
，
即．
为的直径，
是的切线； ———————————————————4分
（2）解：，，
，
设，则，
，，
，
，
是的直径，
，
，
，
解得：不合题意，舍去或．
． ————————————————————8分
23. （本题10分）
解：（1）当时，设甲种蔬菜种植成本y（单位；元/）与其种植面积x（单位：）的函数关系式为，把点代入得，
，
解得，
∴当时，，
当时，，
∴当时，，解得，
即当时，元/；
故答案为：； —————————————————————3分
（2）当时，，
∵，
∴抛物线开口向上，
∴当时，有最小值，最小值为，
当时，，
∵，
∴随着x的增大而减小，
∴当时，有最小值，最小值为，
综上可知，当甲种蔬菜的种植面积为，乙种蔬菜的种植面积为时，W最小；
———————————————————7分
（3）由题意可得，
解得（不合题意，舍去），
∴当a为时，2026年的总种植成本为元．—————————————————10分
24.（本题10分）
（1）解：∵抛物线中，
∴，，
∴抛物线的焦点坐标为，准线l的方程为，
故答案为：，； —————————————————2分
（2）解：由（1）知抛物线的焦点F的坐标为，
∵点到焦点F的距离是它到x轴距离的3倍，
∴，整理得：，
又∵，
∴
解得：或（舍去），
∴，
∴点P的坐标为； ——————————————————4分
（3）解：过点作直线交于点，过点作准线交于点，结合题意和（1）中结论可知，，如图：

若使得取最小值，即的值最小，故当，，三点共线时，，即此刻的值最小；
∵直线与直线垂直，故设直线的解析式为，
将代入解得：，
∴直线的解析式为，
∵点是直线和抛物线的交点，
令，解得：，（舍去），
故点的坐标为，
∴，
∵点是直线和直线m的交点，
令，解得：，
故点的坐标为，
∴，
．
即的最小值为． ————————————————————7分
（4）解：∵抛物线中，
∴，，
∴抛物线的焦点坐标为，准线l的方程为，
过点作准线交于点，结合题意和（1）中结论可知，则，如图：

若使得取最小值，即的值最小，故当，，三点共线时，，即此刻的值最小；如图：

∵点的坐标为，准线，
∴点的横坐标为，代入解得，
即，，
则的面积为． —————————————————10分
注意：评分标准仅做参考，只要学生作答正确，均可得分。对于解答题目，答案错误原则上得分不超过分值的一半，有些题目有多种方法，只要做对，即可得分。另外请各位阅卷老师仔细核对答案，如有问题，请及时更正。