【二轮复习】2024年中考数学 题型5 圆的相关证明与计算（复习讲义）

这是一份【二轮复习】2024年中考数学 题型5 圆的相关证明与计算（复习讲义），文件包含二轮复习2024年中考数学题型5圆的相关证明与计算复习讲义教师版docx、二轮复习2024年中考数学题型5圆的相关证明与计算复习讲义学生版docx等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。

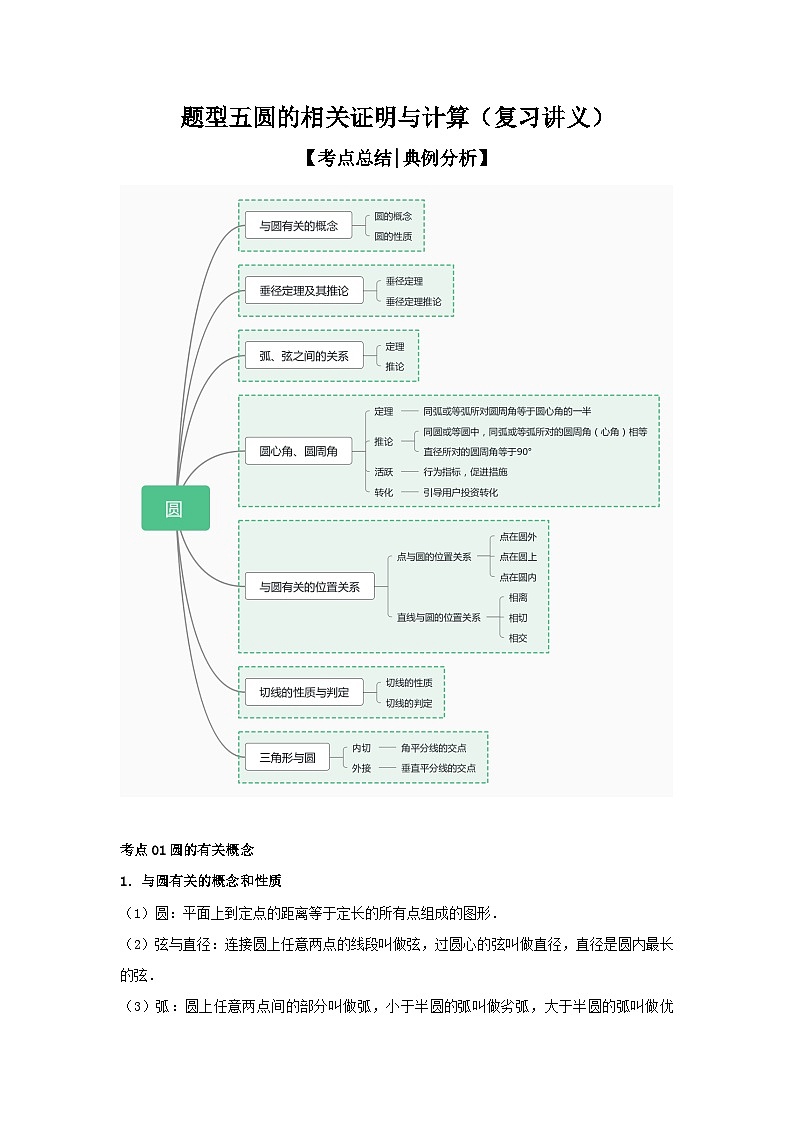
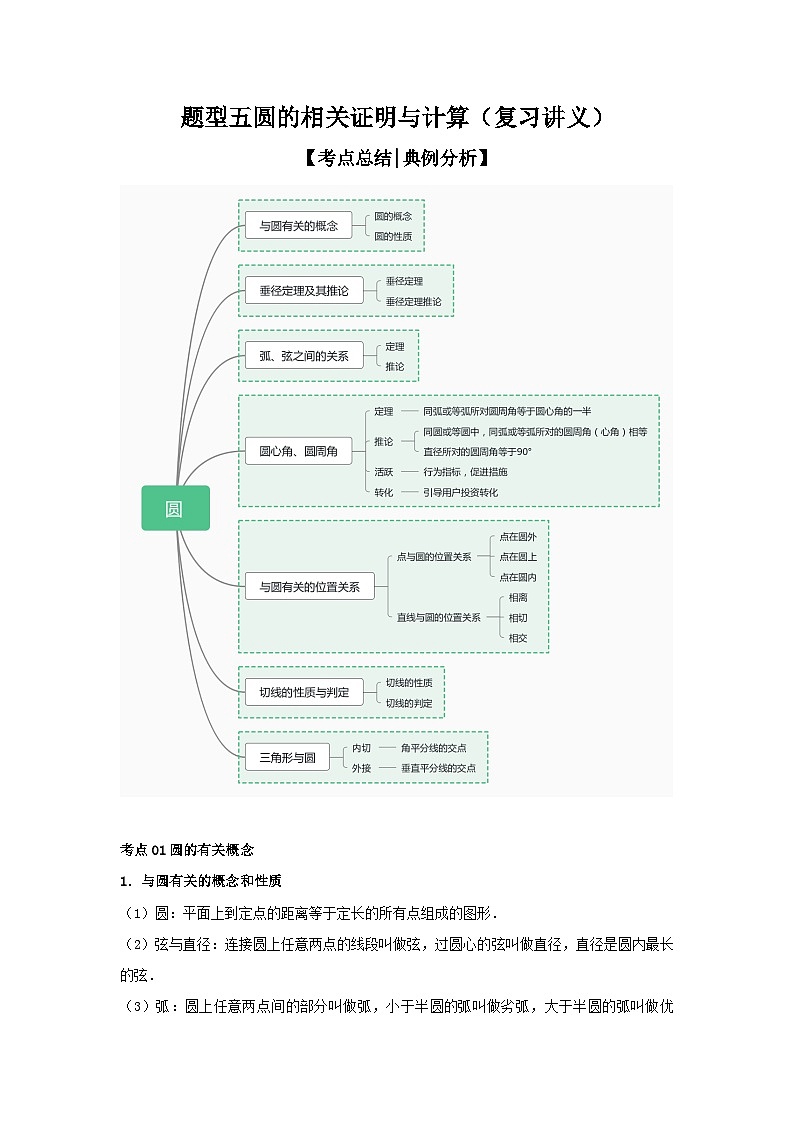
考点01圆的有关概念
1．与圆有关的概念和性质
（1）圆：平面上到定点的距离等于定长的所有点组成的图形．
（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．
（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．
（4）圆心角：顶点在圆心的角叫做圆心角．
（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．
（6）弦心距：圆心到弦的距离．
考点02垂径定理及其推论
1．垂径定理
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．
2．推论
（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；
（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．
考点03圆心角、弧、弦的关系
1．定理
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．
2．推论
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
考点04圆周角定理及其推论
1．定理
一条弧所对的圆周角等于它所对的圆心角的一半．
2．推论
（1）在同圆或等圆中，同弧或等弧所对的圆周角相等．
（2）直径所对的圆周角是直角．
考点05与圆有关的位置关系
1．点与圆的位置关系
设点到圆心的距离为d．
(1)d(2)d=r⇔点在⊙O上；
(3)d>r⇔点在⊙O外．
判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．
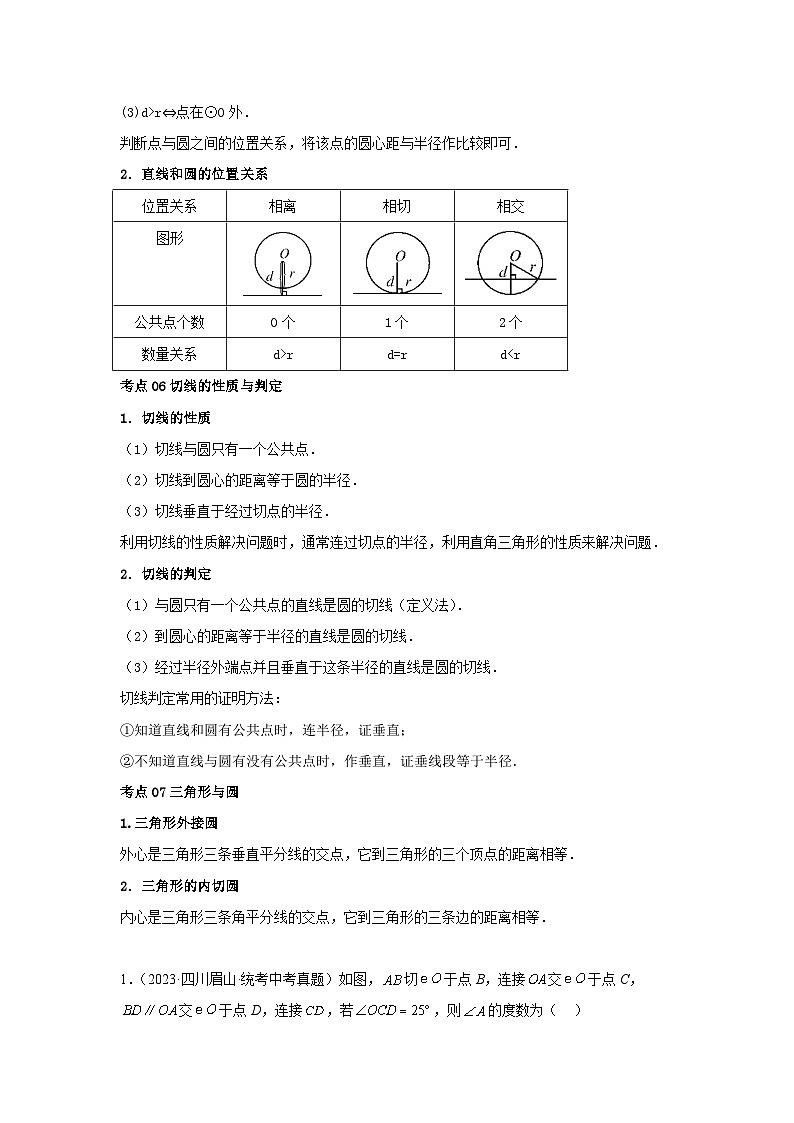
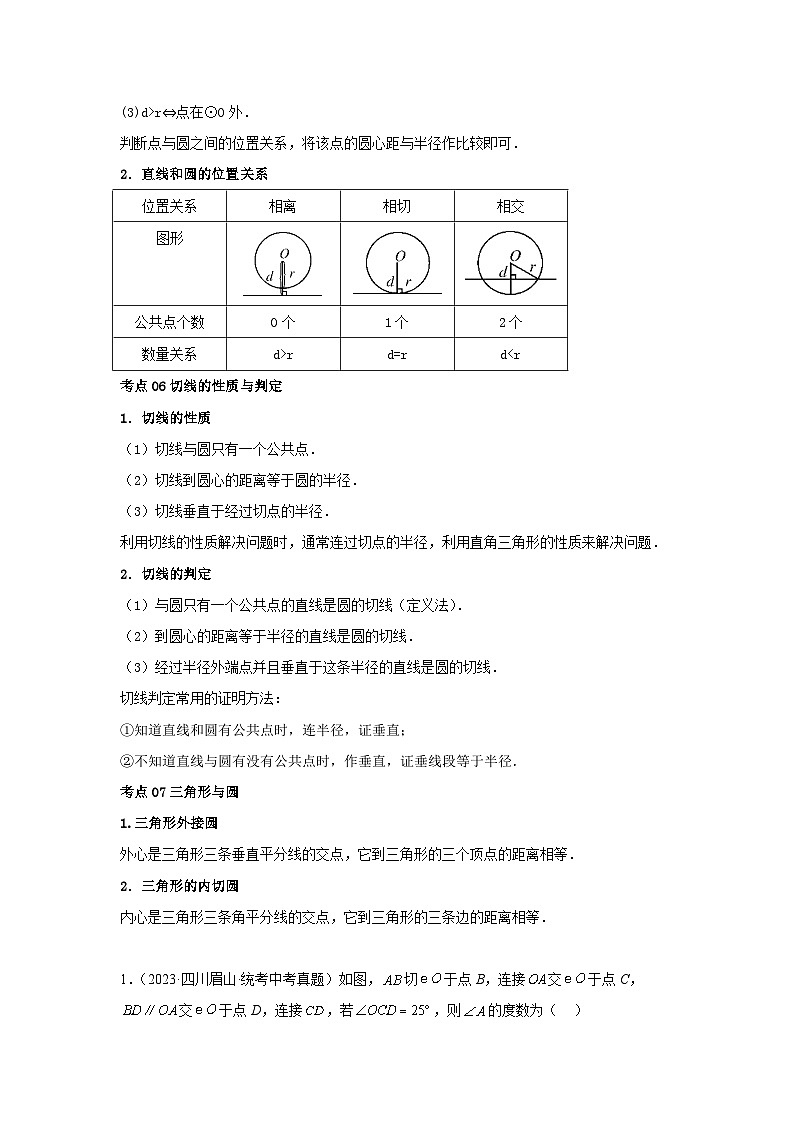
2．直线和圆的位置关系
考点06切线的性质与判定
1．切线的性质
（1）切线与圆只有一个公共点．
（2）切线到圆心的距离等于圆的半径．
（3）切线垂直于经过切点的半径．
利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题．
2．切线的判定
（1）与圆只有一个公共点的直线是圆的切线（定义法）．
（2）到圆心的距离等于半径的直线是圆的切线．
（3）经过半径外端点并且垂直于这条半径的直线是圆的切线．
切线判定常用的证明方法：
①知道直线和圆有公共点时，连半径，证垂直；
②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．
考点07三角形与圆
1.三角形外接圆
外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等．
2．三角形的内切圆
内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等．
1．（2023·四川眉山·统考中考真题）如图，切于点B，连接交于点C，交于点D，连接，若，则的度数为（ ）

A．B．C．D．
2．（2023·重庆·统考中考真题）如图，为的直径，直线与相切于点C，连接，若，则的度数为（ ）

A．B．C．D．
3．（2023·四川自贡·统考中考真题）如图，内接于，是的直径，连接，，则的度数是（ ）
A．B．C．D．
4．（2023·江苏苏州·统考中考真题）如图，是半圆的直径，点在半圆上，，连接，过点作，交的延长线于点．设的面积为的面积为，若，则的值为（ ）

A．B．C．D．
5.如图，A，B，C是半径为1的⊙O上的三个点，若AB＝，∠CAB＝30°，则∠ABC的度数为（ ）
A．95°B．100°C．105°D．110°
6．（2023·四川宜宾·统考中考真题）如图，已知点在上，为的中点．若，则等于（ ）

A．B．C．D．
7.如图，AB是⊙O的直径，AC，BC是⊙O的弦，若，则的度数为（ ）
A．70°B．90°C．40°D．60°
8.如图，中，，，．点为内一点，且满足．当的长度最小时，的面积是（ ）
A．3B．C．D．
9．（2023·湖南常德·统考中考真题）如图，四边形是的内接四边形，是直径，是的中点，过点作交的延长线于点．

(1)求证：是的切线；
(2)若，，求的长．
10．（2023·湖南张家界·统考中考真题）如图，是的外接圆，是的直径，是延长线上一点，连接，且．
(1)求证：是的切线；
(2)若直径，求的长．
11.如图，A，B是上两点，且，连接OB并延长到点C，使，连接AC．
（1）求证：AC是的切线．
（2）点D，E分别是AC，OA的中点，DE所在直线交于点F，G，，求GF的长．
12．（2023·辽宁·统考中考真题）如图，是的直径，点在上，，点在线段的延长线上，且．

(1)求证：EF与相切；
(2)若，求的长．
13．（2023·浙江金华·统考中考真题）如图，点在第一象限内，与轴相切于点，与轴相交于点．连接，过点作于点．

(1)求证：四边形为矩形．
(2)已知的半径为4，，求弦的长．
14.如图，在中，是直径，弦，垂足为，为上一点，为弦延长线上一点，连接并延长交直径的延长线于点，连接交于点，若．
（1）求证：是的切线；
（2）若的半径为8，，求的长．
15．（2023·四川成都·统考中考真题）如图，以的边为直径作，交边于点D，过点C作交于点E，连接．

(1)求证：；
(2)若，求和的长．
16.如图，是的内接三角形，是的直径，点是的中点，交的延长线于点．
（1）求证：直线与相切；
（2）若的直径是10，，求的长．
20.如图，已知点是以为直径的圆上一点，是延长线上一点，过点作的垂线交的延长线于点，连结，且．
（1）求证：是的切线；
（2）若，，求的半径．
21.（2023·上海·统考中考真题）如图，在中，弦的长为8，点C在延长线上，且．

(1)求的半径；
(2)求的正切值．
22.如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D是直径AB延长线上一点，且∠BCE＝∠BCD．
（1）求证：CD是⊙O的切线；
（2）若AD＝8，BECE=12，求CD的长．
23.如图，△ABC内接于⊙O，AB为⊙O的直径，AB＝10，AC＝6，连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．
（1）求证：∠CAD＝∠CBA．
（2）求OE的长．
24．（2023·辽宁大连·统考中考真题）如图1，在中，为的直径，点为上一点，为的平分线交于点，连接交于点．

(1)求的度数；
(2)如图2，过点作的切线交延长线于点，过点作交于点．若，求的长．
25．（2023·黑龙江齐齐哈尔·统考中考真题）如图，在中，，平分交于点D，点E是斜边上一点，以为直径的经过点D，交于点F，连接．

(1)求证：是的切线；
(2)若，，求图中阴影部分的面积（结果保留π）．
26.如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．
（1）求证：DC∥AP；
（2）求AC的长．
27．（2023·湖北武汉·统考中考真题）如图，都是的半径，．

(1)求证：；
(2)若，求的半径．
28.如图，AB为⊙O的直径，C、D为⊙O上的两个点，AC=CD=DB，连接AD，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线．
（2）若直径AB＝6，求AD的长．
29．（2023·湖南·统考中考真题）如图，是的直径，是一条弦，D是的中点，于点E，交于点F，交于点H，交于点G．

(1)求证：．
(2)若，求的半径．
30.如图，AB是半圆O的直径，C，D是半圆O上不同于A，B的两点，AD＝BC，AC与BD相交于点F．BE是半圆O所在圆的切线，与AC的延长线相交于点E．
（1）求证：△CBA≌△DAB；
（2）若BE＝BF，求证：AC平分∠DAB．
31.如图，AB为⊙O的直径，C为⊙O上一点，AD与过C点的直线互相垂直，垂足为D，AC平分∠DAB．
（1）求证：DC为⊙O的切线．
（2）若AD＝3，DC=3，求⊙O的半径．
32.如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作⊙O的切线交AC于点E．
（1）求证：DE⊥AC；
（2）若⊙O的半径为5，BC＝16，求DE的长．
位置关系
相离
相切
相交
图形
公共点个数
0个
1个
2个
数量关系
d>r
d=r
d