专题2.3(1) 矩形的折叠问题中考数学二轮复习必会几何模型剖析（全国通用）课件PPT

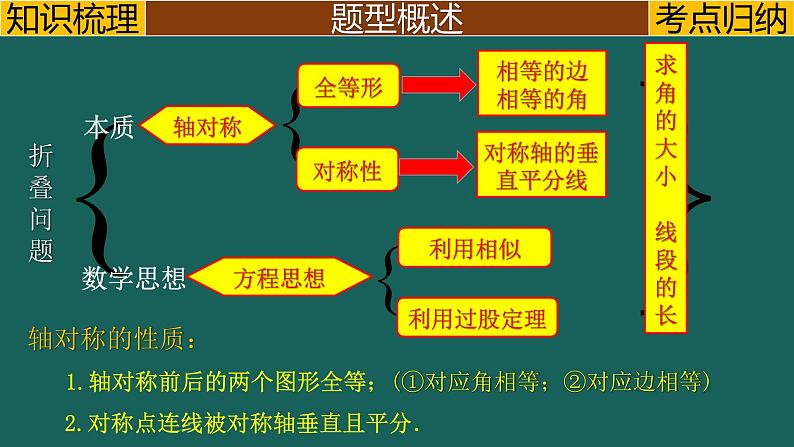
这是一份专题2.3(1) 矩形的折叠问题中考数学二轮复习必会几何模型剖析（全国通用）课件PPT，共19页。PPT课件主要包含了折叠问题，数学思想，轴对称，方程思想，全等形，对称性，相等的边相等的角，对称轴的垂直平分线，利用相似，利用过股定理等内容，欢迎下载使用。
求角的大小 线段的长
1.轴对称前后的两个图形全等；(①对应角相等；②对应边相等)
2.对称点连线被对称轴垂直且平分．
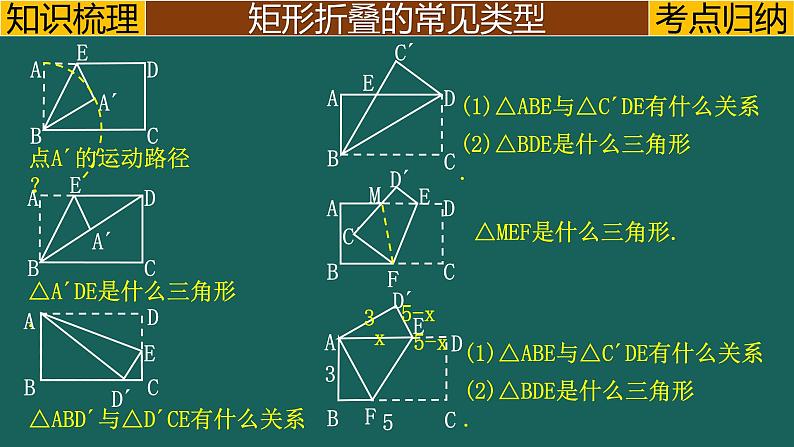
△ABD´与△D´CE有什么关系
(1)△ABE与△C´DE有什么关系
(2)△BDE是什么三角形.
△A´DE是什么三角形.
△MEF是什么三角形.
【分析】根据图形位置的特殊性,寻找隐含条件.
根据点Q在EF上且∠BQP=90º.
∴∠ABQ=∠PBQ=∠CBP=30º.
【小结】从中点处翻折,则另外部分亦可翻折.
【分析】有特殊位置关系必然有隐藏结论.
连接CE,易证△CED≌△CEG(HL).
易证△CDE∽△EAF,
13.如图,四边形ABCD是矩形纸片,将△BCD沿BD折叠,得到△BED,BE交AD于点F,AB=3,AF:FD=1:2,则AF=____.
x2-32=(2x)2,
【分析】易证△AFB≌△EFD.
【小结】沿对角线折叠,则必有一组全等.
设AF=x,则BF=DF=2x,又AB=3.
故x2-32=(2x)2,
【小结】对称点落在矩形外,也可能有全等,有相等线段便可用用勾股与相似.
【分析】根据0P=0F,易证△0EF≌△0BP,
∴0E=0B,0E+0P=0B+0F,即EP=BF.
设EP=BF=x,则AF=4-x,
∴EF=BP=3-x,
∴DF=4-(3-x)=x+1.
在Rt△ADF中,DF2=AD2+AF2,
代入得：(x+1)2=3+(4-x)2
【分析】与上题类似,分析出P点轨迹.
∵S△PAB=0.5S△PCD.
∵过点P作MN∥AB分别交AD、BC于M、N两点.
则M是线段AD靠近点A的三等分点,N是线段BC靠近点B的三等分点.
作点D关于MN的对称点D´,连接CD´,与MN交点即为P点.
1.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论：①∠EBG=45º；②△DEF∽△ABG；③AG+DF=FG；④S△ABG=1.5S△FGH.其中正确的是_______.(填序号)
2.如图,正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为____.
∴PM-PN的最大值为2.
【分析】求两线段差值最大的思路是“三角形两边之差小于第三边，当三点共线时差最大”，
本题的难点在于无论P在对角线BD的任何位置,都无法构造出PM-PN=MN.
作点M关于BD的对称点M´,
根据正方形的对称性可得点M´在边AB上且AM´=CM=2,
∴PM-PN=PM´-PN≤M´N,当M´、N、P共线时取到等号.
∴M´N=AM´=2,
1.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG＞60º.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为____.2.如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D´、C´的位置,若∠EFB=65º,则∠AED´=____º.
3.如图,在坐标系中,把矩形OABC的顶点O放在原点处,把边OA,OC分别放在x轴、y轴的正半轴上,点D在OC边上,把△BDC沿直线BD翻折,点C的对应点恰好落在x轴上的点E处,已知B(10,8),则直线BD的解析式为________. 4.如图,四边形ABCD是矩形,AB:AD=4:3,把矩形沿直线AC折叠,点B落在点E处,连接DE,则DE:AC=( )A.1:3 B.3:8 C.8:27 D.7:25
5.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=____．6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( ) A.1 B.1.5 C.2 D.2.5
x2-22=(4-x)2
(3x)2-52=(4x)2
9.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为___.10.如图,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP=____.
【分析】根据对称的性质.
∴∠KEG=67.5º,∠KEF=45º.
∴∠KFH=75º,∠KFE=30º,
过点K作KP⊥BC交BC于P点，
综上所述,CE的长为2.5或10.
【分析】可能情况如下：
由题意可得：DC´=DC=5,DM=4,
∴MC´=3,C´N=2.
对于△ENC´,设CE=x,
则C´E=x,EN=4-x.
(4-x)2+22=x2,
易证C´F=CD=5,
∴NF=3,MF=2.
易证EN=4×1.5=6.