专题5.3 相似---X字形及其变形中考数学二轮复习必会几何模型剖析（全国通用）课件PPT

这是一份专题5.3 相似---X字形及其变形中考数学二轮复习必会几何模型剖析（全国通用）课件PPT，共25页。PPT课件主要包含了∴DF6cm，∴△EDF∽△CBF，∴AEDE32，∴DEAD25，∵BF15，∴DEBC25，∴∠BAD＝∠AED，∴CFDF，2∵∠A∠D，∵AEBE等内容，欢迎下载使用。
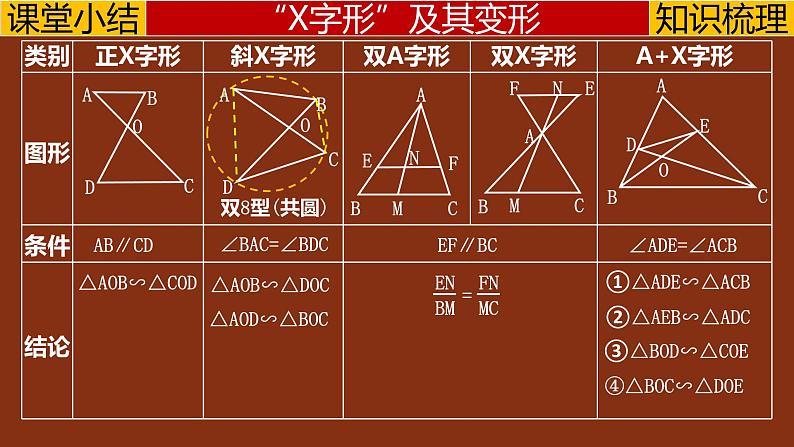
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.相似和勾股是产生等式的主要依据(其他依据还有面积法,三角函数等),因此要掌握相似三角形的基本图形,体会其各种 演变和联系.现将基本模型总结如下： 模型一 A字形； 模型二 X(8)字形； 模型三 K字形。
对于“A字形”及“ X字形”(或作平行线或其他辅助线去构造“AX字形”)问题，一般利用平行线分线段成比例定理或相似三角形的判定、性质去进行比例变形、等量代换，寻找中间比，从而将问题解决.
【例1】如图,已知E是□ABCD中AD边上一点,且AE:DE=3:2,CE交BD于点F,BF=15cm,求DF的长.
解：∵四边形ABCD是平行四边形.
∴BC∥AD,BC=AD
∴DF:BF=DE:BC
【例2】如图,已知在△ABC中,BE平分∠ABC交AC于点E,点D在BE的延长线上,且BA·BC=BD·BE. (1)求证：△ABD∽△EBC. (2)求证：AD2=BD·DE
即：AD2＝BD·DE.
证明：(1)∵BE平分∠ABC，
∴∠ABD=∠EBC.
∵BA·BC=BD·BE，
∴AB:BE=BD:BC.
∴△ABD∽△EBC.
(2)∵△ABD∽△EBC，
∴∠BAD＝∠BEC.
∵∠EAD＝∠BEC，
∵∠ADE＝∠ADB，
∴△AED∽△BAD.
∴AD:BD=DE:AD
【例3】如图,AD与BC相交于点O,EF过点O,交AB于点E,交CD于点F,BO=1,CO=3,AO=1.5,DO=4.5. (1)求证：∠A=∠D. (2)若AE=BE,求证：CF=DF.
证明：(1)∵BO=1,CO=3,AO=1.5,DO=4.5,
∴OB:OC=OA:OD.
∵∠AOB=∠COD,
∴△OAB∽△ODC.
∴AE:DF=OE:OF,BE:CF=OE:OF.
∴AE:DF=BE:CF.
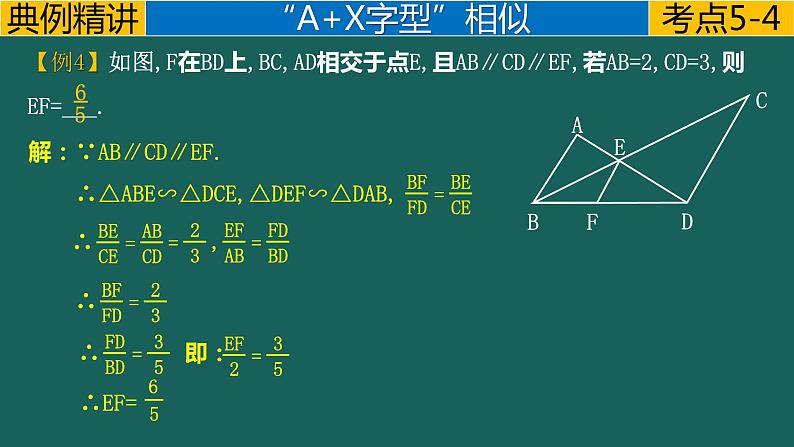
【例4】如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF,若AB=2,CD=3,则EF=___.
解：∵AB∥CD∥EF.
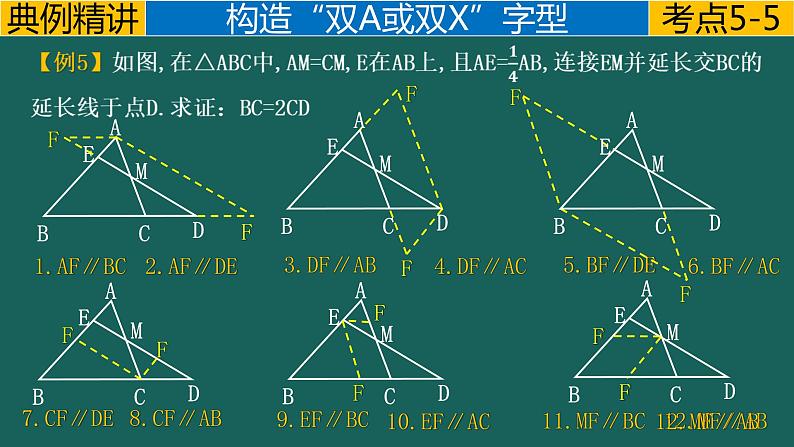
【例2-4】如图,在△ABC中,D,E分别是AB,AC上的点,且BD=2AD,CE=2AE. (1)求证：△ADE∽△ABC. (2)若DF=2,求FC的长度.
(1)证明：∵BD=2AD,CE=2AE，
∴AD:AB=AE:AC=1:3.
∵∠DAE=∠BAC,
∴△ADE∽△ABC.
(2)解：∵△ADE∽△ABC，
∴DE:BC=AD:AB=1:3,∠ADE＝∠ABC.
∴△DEF∽△CBF.
∴DF:CF=DE:CB 即2：CF=1:3
5.如图,AM:MD=4:1,BD:DC=2:3,则AE:EC=_____.6.如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于点E,则BE:EC=_____.
7.如图：已知等边△ABC,D为AC边上的一动点,CD=nDA,连线段BD,M为线段BD上一点,∠AMD=60º,AM交BC于E.(1)若n=1,则BE:CE=____.BM:DM=____；(2)若n=2,求证：BM=6DM；
证明：∵△ABC的高AD、BE交于点F，
∴∠FEA=∠FDB=90º,∠AFE=∠BFD.
∴△FEA∽△FDB，
∴△ADC∽△BEC；
10.如图,在△ABC中,∠ABC＝90º,∠C＝30º,D为BC上一点,DE⊥AC于点E. (1)求证：△ADC∽△BEC；(2)若点D为BC的中点,AB=4,求BE的长.
(1)证明：∵在四边形ABDE中,∠ABD+∠AED=180º.
∴∠BAE+∠BDE=180º.
∴点A、B、D、E四点共圆.
∴∠DAE=∠DBE.
(2)解：∵AB=4,∠C=30º,∠ABC=90º.
在Rt△CDE中，∠C=30º,CD=2.
∵△ADC∽△BEC.
11.如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.(1)若FD=2,ED:BC＝1:3,求线段DC的长；(2)求证：EF·GB＝BF·GE.
2.在△ABC中,点P为边AB上一点. (1)如图1,若∠ACP=∠B,求证：AC2=AP·AB； (2)如图2,点M为CP的中点,AC=2,∠PBM=∠ACP,AB=3.求BP的长.
【变式】已知:如图,∠ABD=∠C,AD=2且AC=8,求AB长.