甘肃省陇南市礼县礼县第一中学2023-2024学年七年级下学期期中数学试题

这是一份甘肃省陇南市礼县礼县第一中学2023-2024学年七年级下学期期中数学试题，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

注意事项：本试卷满分为150分，考试时间为120分钟．所有试题均在答题卡上作答，否则无效．
一、选择题（本大题共10小题，每小题3分，共30分．每小题只有一个正确选项）
1. 8的算术平方根是（ ）
A. 2B. C. D. 4
【答案】C
【解析】
【分析】根据算术平方根的定义：若，那么b就叫做a的算术平方根求解即可．
【详解】解：∵，
∴8的算术平方根为，
故选C．
【点睛】本题主要考查了求一个数的算术平方根，熟知算术平方根的定义是解题的关键．
2. 下列实数中是无理数的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查的知识点是无理数，解题关键是熟练掌握无理数的概念．
无理数：指无限不循环小数，据此即可求解．
【详解】选项，是有理数，不符合题意，选项错误；
选项，是有限小数，是有理数，不符合题意，选项错误；
选项，是有理数，不符合题意，选项错误；
选项，是无限不循环小数，符合题意，选项错误．
故选：．
3. 如图，把一块直角三角板的直角顶点放在直尺的一边上．若，则的度数是（ ）该试卷源自 全站资源不到一元，每日更新。
A. 22°B. 32°C. 42°D. 52°
【答案】B
【解析】
【分析】由两直线平行，同位角相等，可求得的度数，然后求得的度数.
【详解】如图，
，
，
.
故选.
【点睛】此题考查了平行线的性质，两直线平行，同位角相等的应用是解此题的关键.
4. 若点P的坐标为（7，﹣6），则点P必在（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】D
【解析】
【分析】四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣），再根据点P的坐标的符号，即可得出答案．
【详解】解：∵点P的坐标为（7，﹣6），
∴点P所在的象限是第四象限．
故选D．
【点睛】此题考查点的坐标，解题关键在于掌握其性质.
5. 电影票上的“2排5号”如果用（2，5）表示，那么“5排2号”应该表示为（ ）
A. （2，5）B. （5，2）C. （-5，-2）D. （-2，-5）
【答案】B
【解析】
【详解】∵(2,5)表示2排5号，
∴5排2号的电影票可表示为(5,2).
故选B.
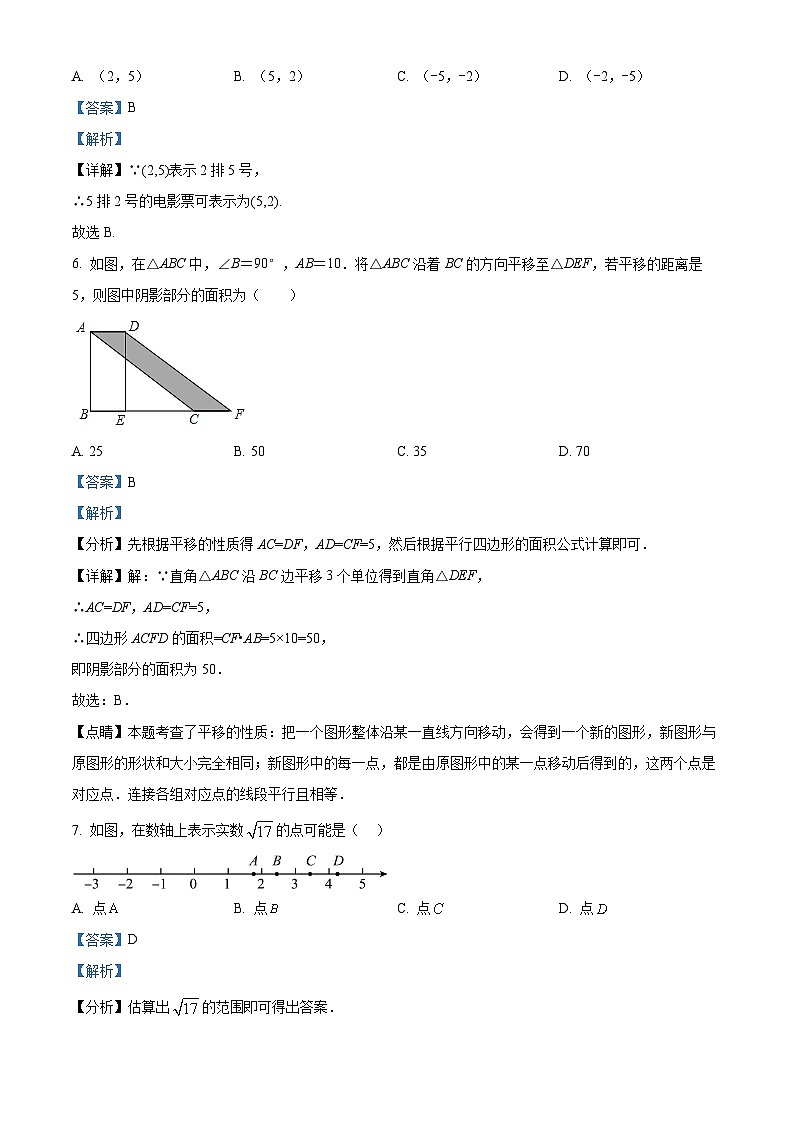
6. 如图，在△ABC中，∠B＝90°，AB＝10．将△ABC沿着BC的方向平移至△DEF，若平移的距离是5，则图中阴影部分的面积为（ ）
A. 25B. 50C. 35D. 70
【答案】B
【解析】
【分析】先根据平移的性质得AC=DF，AD=CF=5，然后根据平行四边形的面积公式计算即可．
【详解】解：∵直角△ABC沿BC边平移3个单位得到直角△DEF，
∴AC=DF，AD=CF=5，
∴四边形ACFD的面积=CF•AB=5×10=50，
即阴影部分的面积为50．
故选：B．
【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．
7. 如图，在数轴上表示实数的点可能是（ ）
A. 点B. 点C. 点D. 点
【答案】D
【解析】
【分析】估算出的范围即可得出答案．
【详解】解：∵，
∴，
∴．
故选：D．
【点睛】本题考查无理数的估算，无理数的估算常用夹逼法．用有理数夹逼无理数是解题的关键．涉及算术平方根的大小比较．
8. 下列命题可作为真命题的有（ ）
①两直线平行，同位角相等；②垂线段最短；③相等的角是对顶角；④同角的余角相等；⑤内错角相等；⑥两点确定一条直线．
A. 4个B. 3个C. 2个D. 1个
【答案】A
【解析】
【分析】利用平行线的性质及判定方法、对顶角的定义、余角的性质、确定直线的条件等知识分别判断后即可确定正确的选项．
【详解】解∶ ①两直线平行，同位角相等，正确，是真命题，符合题意；
②直线外一点到直线上所用点的连线中，垂线段最短，简称“垂线段最短”，正确，是真命题，符合题意；
③相等的角不一定是对顶角，故错误，是假命题，不符合题意；
④同角的余角相等，正确，是真命题，符合题意；
⑤两直线平行，内错角相等，故错误，是假命题，不符合题意；
⑥两点确定一条直线，正确，是真命题，符合题意．
故选∶A．
【点睛】本题考查了命题与定理的知识，解题的关键是熟记平行线的性质及判定方法、对顶角的定义、、余角的性质、确定直线的条件等知识．
9. 若，则的值为（ ）
A. B. C. 3D. 1
【答案】C
【解析】
【分析】此题主要考查了非负数的性质，正确得出，的值是解题关键．直接利用非负数的性质进而得出，的值，进而得出答案．
【详解】解：，
，，
，，
．
故选：C
10. 在实数范围内定义运算“”：，例如：．若代数式的值是17，则的值为（ ）
A. 2B. 4C. 8D.
【答案】D
【解析】
【分析】本题考查了新定义下的实数运算，代数式求值．理解新定义是解题的关键．
由，可得，由题意知，，进而可得结果．
【详解】解：∵，
∴，
由题意知，，
故选：D．
二、填空题（本大题共6小题，每小题4分，共24分）
11. 已知，则x=______．
【答案】3
【解析】
【分析】根据立方根解方程即可求解．
【详解】解：∵，
∴
解得
故答案为：
【点睛】本题考查了立方根的定义，掌握立方根的定义是解题的关键．
12. 一个正数的两个平方根分别为和，则这个数为___．
【答案】1
【解析】
【分析】由“一个正数的两个平方根互为相反数”得到a+3+2a+3=0，据此可以求得a的值，即可求解．
【详解】解：根据题意，得
a+3+2a+3=0，即3a=-6，
解得，a=-2
这个数为1
故答案是：1．
【点睛】本题考查了平方根的定义．一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根．
13. 如图，已知直线相交于点O，，垂足为O．若，则的度数为__________．

【答案】##度
【解析】
【分析】先根据垂直的定义得到，进而求出，再根据平角的定义即可求出答案．
【详解】解：∵，
∴，
∵，
∴，
∴，
故答案为：．
【点睛】本题主要考查了垂直的定义，平角的定义，正确求出是解题的关键．
14. 如图，直线AB∥CD，∠1=50°，∠2=110°，那么∠E=__度．
【答案】60
【解析】
【详解】
∵AB∥CD，∴∠2=∠3=110°，
∵∠3=∠1+∠E，∠1=50°，∴∠E=60°.
故答案为60.
15. 在平面直角坐标系中，把点向左平移2个单位长度，再向下平移3个单位长度，平移后点的坐标为______．
【答案】
【解析】
【分析】本题考查坐标与图形的平移，根据横坐标，右移加，左移减；纵坐标，上移加，下移减的规律即可解决问题．
【详解】解：点向左平移2个单位长度，再向下平移3个单位长度，可得点的坐标，即，
故答案：．
16 若＝2.468，＝24.68，那么a＝_____．
【答案】15.03．
【解析】
【分析】根据＝2.468，＝24.68，可得：a＝2.4683，24.683＝15030，据此求出a的值是多少即可．
【详解】∵＝2.468，＝24.68，
∴a＝2.4683，24.683＝15030，
∴a＝15030÷1000＝15.03．
故答案为：15.03．
【点睛】此题主要考查了立方根的性质和应用，要熟练掌握，解答此题的关键是要明确：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0．
三、解答题（本大题共6小题，共46分，解答时，应写出必要的文字说明、证明过程或演算步骤）
17. 计算：．
【答案】
【解析】
【分析】根据实数相关计算规则，分步计算即可．
【详解】解：
【点睛】本题考查了实数的有关运算，涉及了算术平方根、立方根以及绝对值的求解，熟练掌握相关求解方法是解题的额关键．
18. 如图，直线 ，， 相交于点 ．
（1）写出的邻补角．
（2）写出，的对顶角．
（3）如果，求，的度数．
【答案】（1）的邻补角为或 ．
（2） 的对顶角为，的对顶角为．
（3），
【解析】
【分析】（1）根据邻补角定义：只有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角进行分析；
（2）根据对顶角定义：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线进行分析即可；
（3）根据邻补角互补、对顶角相等可得答案．
【小问1详解】
解：的邻补角是：，；
【小问2详解】
的对顶角是，的对顶角是；
【小问3详解】
，
，．
【点睛】此题主要考查了邻补角和对顶角，关键是掌握邻补角和对顶角定义和性质．
19. 某金属冶炼厂将27个大小相同的正方体钢锭在炉中熔化后浇铸成一个长方体钢锭，量得这个长方体钢锭的长、宽、高分别为160cm、80cm和40cm，求原来正方体钢锭的棱长.
【答案】 cm.
【解析】
【分析】设原来正方体钢锭的棱长为xcm，根据题意列出方程，解方程即可得到结果．
【详解】解：设原来正方体钢锭棱长为xcm，
则，
解得.
答：原来正方体钢锭的棱长为cm.
【点睛】本题考查立方根的应用，熟练掌握立方根的定义是解本题的关键．
20. 已知的立方根是，的算术平方根是4，求的平方根．
【答案】
【解析】
【分析】根据立方根和算术平方根的定义可得，，由此求出a、b的值，从而求出a+2b的值，再根据平方根的定义求解即可．
【详解】解：的立方根是，的算术平方根是4，
，，
，
，
的平方根是．
【点睛】本题主要考查了算术平方根，立方根和平方根的定义，熟知三者的定义是解题的关键．
21. 如图，这是某市部分简图，为了确定各建筑物的位置；
（1）请你以火车站为原点建立平面直角坐标系．
（2）写出体育场、宾馆、超市的坐标．
（3）图书馆的坐标为，请在图中标出图书馆的位置．
【答案】（1）见解析 （2）体育场的坐标为、宾馆的坐标为、超市的坐标为
（3）见解析
【解析】
【分析】（1）按要求建立直角坐标系即可；
（2）结合（1）中的坐标系，直接找到对应坐标即可；
（3）根据坐标直接描点即可．
【小问1详解】
如图所示：
坐标系即为所得；
小问2详解】
根据上图可得：体育场的坐标为、宾馆的坐标为、超市的坐标为；
【小问3详解】
图书馆的位置如图所示．
【点睛】本题考查了平面直角坐标系的建立，与点的坐标的书写，由于所写点的位置比较多，可以根据象限的顺序依次写出，避免重写或漏写．
22. 如图，，，，试证明：，请将下面的证明过程补充完整．
证明：∵（____________________），
∴____________________（____________________），
∵（____________________），
∴____________________（等量代换），
又∵（____________________），
∴（____________________），
∵（____________________），
∴____________________，
∴（____________________）．
【答案】已知；；两直线平行，同位角相等；已知；；对顶角相等；等量代换；已知；；同旁内角互补，两直线平行
【解析】
【分析】根据平行线的判定和性质进行解答即可．
本题主要考查了平行线的判定和性质，对顶角性质，解题的关键是熟练掌握平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．平行线的判定：内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补，两直线平行．
【详解】证明：∵（已知），
∴（两直线平行，同位角相等），
∵（已知），
∴（等量代换），
又∵（对顶角相等），
∴（等量代换），
∵（已知），
∴，
∴（同旁内角互补，两直线平行）．
故答案为：已知；；两直线平行，同位角相等；已知；；对顶角相等；等量代换；已知；；同旁内角互补，两直线平行．
四、解答题（本大题共5小题，共50分，解答时，应写出必要的文字说明、证明过程或演算步骤）
23. 如图所示，平面直角坐标系中，的三个顶点都在网格点上，其中点的坐标是．
（1）直接写出点、的坐标；
（2）三角形的面积是多少？
（3）将先向左平移3个单位长度，再向上平移2个单位长度，得到，并在坐标系中画出，写出三点的坐标．
【答案】（1），
（2）；
（3）图见解析，．
【解析】
【分析】（1）根据直角坐标系的特点写出点的坐标；
（2）利用所在长方形的面积减去周围三角形的面积，即可求出△ABC的面积；
（3）分别将点A、B、C先向左平移3个单位长度，再向上平移2个单位长度，得到点，然后顺次连接得到，写出坐标即可．
【小问1详解】
解：由A，B在直角坐标系中的位置可知：，；
【小问2详解】
解：根据图形可知，
；
【小问3详解】
解：的位置如图所示：
∴．
【点睛】本题考查了坐标与图形，图形的平移，利用网格计算图形的面积等，解题的关键是熟练掌握网格结构特征和平移变换的性质．
24. 已知点．
（1）若点P在x轴上，求m的值；
（2）若点P到x轴的距离是到y轴距离的2倍，求P点的坐标．
【答案】（1）1 （2）或
【解析】
【分析】（1）根据轴上点的特征即可求得答案．
（2）根据点的坐标轴的距离性质可联立等量关系即可求得答案．
【小问1详解】
解：∵点在x轴上，
∴，
解得：．
【小问2详解】
解∶∵点P到x轴的距离是到y轴距离的2倍，
∴，
∴或，
解得：或7，
∴P点的坐标为或．
【点睛】此题主要考查了点的坐标，正确掌握平面内点的坐标特点，能够正确分类讨论是解题的关键．
25. 如图，AB∥CD，AM平分∠BAE，FG平分∠AFC．
（1）求证：AM∥GF；
（2）若∠BAM＝55°，求∠CFE的度数．
【答案】（1）见解析；
（2）70°
【解析】
【分析】（1）根据ABCD及角平分线的定义得到∠MAE=∠AFG，即可证得AMGF；
（2）利用角平分线的性质求出∠BAE=2∠BAM＝110°，根据平行线的性质求出∠DFE=∠BAE=110°，即可求出∠CFE．
【小问1详解】
证明：∵ABCD，
∴∠BAE=∠AFC，
∵AM平分∠BAE，FG平分∠AFC．
∴∠MAE=∠BAE，∠AFG=∠AFC，
∴∠MAE=∠AFG，
∴AMGF；
【小问2详解】
解：∵∠BAM＝55°，AM平分∠BAE，
∴∠BAE=2∠BAM＝110°，
∵ABCD，
∴∠DFE=∠BAE=110°，
∴∠CFE=180°-∠DFE=70°．
【点睛】此题考查了平行线的性质及判定，角平分线的性质，熟记平行线的性质是解题的关键．
26. 如图，已知，．

（1）试问与相等吗？请说明理由；
（2）若，，求的度数．
【答案】（1）相等，理由见解析
（2）
【解析】
【分析】（1）由平行线的性质可得，结合即可得出内错角相等，进而得出；
（2）由平行线的性质可得，根据题意求出的度数即可解答．
【小问1详解】
解：与相等，理由如下：
∵，
，
，
同角的补角相等，
∴（内错角相等，两直线平行，
两直线平行，同位角相等，
【小问2详解】
解：∵，
，
，，
，即，
，，
，
即．
【点睛】本题考查平行线的性质和判定，熟练掌握平行线的性质和判断是解题关键．
27. 在平面直角坐标系xOy中，对于不同的两点M，N，若点M到x轴，y轴的距离的较大值等于点N到x轴，y轴的距离的较大值，则称点M，N互为“方格点”．
例如：点，互为“方格点”；点，互为“方格点”．已知点．
（1）在点，，中，是点P的“方格点”的是_______；
（2）若点与点P互为“方格点”，求m的值；
（3）若点与点P互为“方格点”，求n的值．
【答案】（1）
（2）或
（3）或
【解析】
【分析】（1）根据“方格点”的定义解答即可；
（2）根据“方格点”的定义，解即可；
（3）分情况讨论，进而求得符合条件的n的值．
【小问1详解】
解：∵点到x轴，y轴的距离的较大值为4，
点到x轴，y轴的距离的较大值为6，
点到x轴，y轴的距离的较大值为4，
点到x轴，y轴的距离的较大值为5，
∴点与点互为“方格点”．
故答案为：．
【小问2详解】
若点与点P互为“方格点”．
当时，，解得；
当时，，解得．
综上，或．
【小问3详解】
若点与点P互为“方格点”，则
①，．
，，
或．
当时，（舍去）；
当时，．
．
②，．
，
或．
当时，；
当时，（舍去）．
．
③，．
或，且或．
无解．
综上，或．
【点睛】本题考查坐标与图形的性质，掌握分类讨论的数学思想是解题关键．