2023-2024学年中考数学全真模拟预测试题（湖南省长沙市适用）

这是一份2023-2024学年中考数学全真模拟预测试题（湖南省长沙市适用），共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．2022的相反数是（ ）
A．2022B．C．D．
2．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．B．C．D．
3．若关于的一元二次方程有两个相等的实数根，则实数的值为（ ）
A．B．C．D．
4．水中涟漪（圆形水波）不断扩大，记它的半径为r，则圆周长C与r的关系式为．下列判断正确的是（ ）
A．2是变量B．是变量C．r是变量D．C是常量
5．已知关于的二元一次方程组的解满足，则m的值为（ ）
A．0B．1C．2D．3
6．如图，在中，一定正确的是（ ）
A．B．C．D．
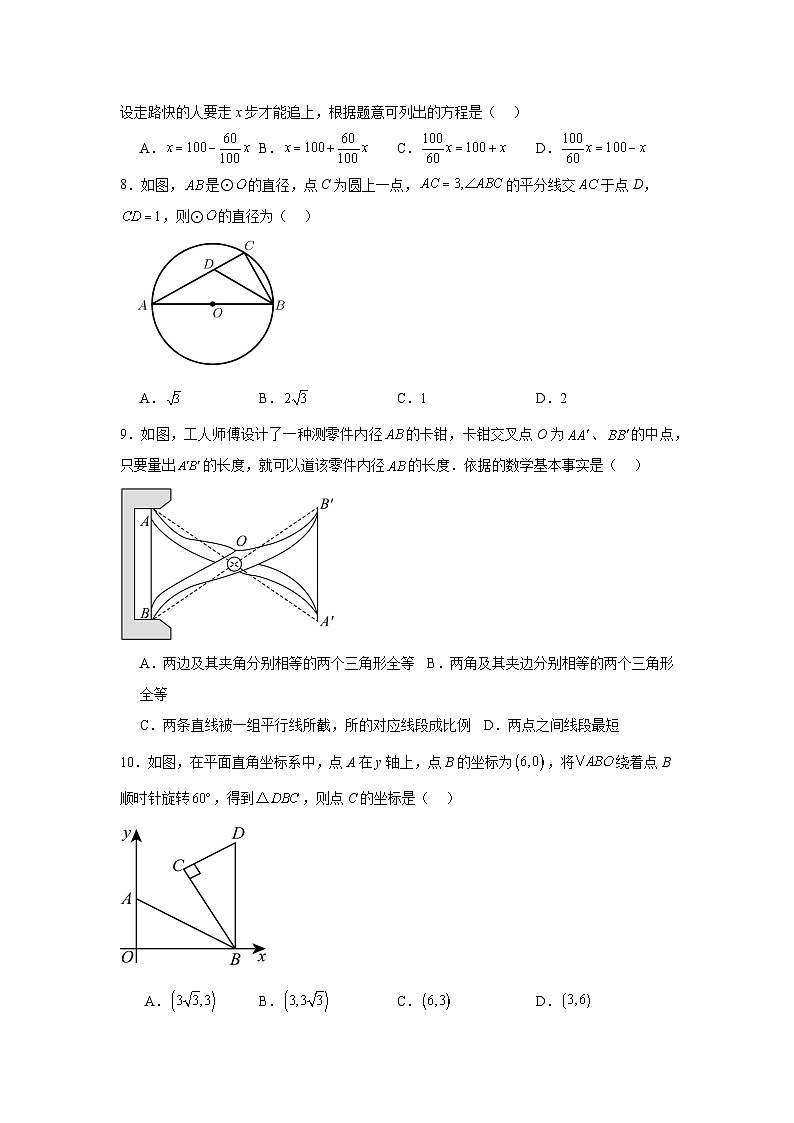
7．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？（注：步为长度单位）”设走路快的人要走x步才能追上，根据题意可列出的方程是（ ）
A．B．C．D．
8．如图，是⊙的直径，点C为圆上一点，的平分线交于点D，，则⊙的直径为（ ）
A．B．C．1D．2
9．如图，工人师傅设计了一种测零件内径的卡钳，卡钳交叉点O为、的中点，只要量出的长度，就可以道该零件内径的长度．依据的数学基本事实是（ ）
A．两边及其夹角分别相等的两个三角形全等B．两角及其夹边分别相等的两个三角形全等
C．两条直线被一组平行线所截，所的对应线段成比例D．两点之间线段最短
10．如图，在平面直角坐标系中，点A在y轴上，点B的坐标为，将绕着点B顺时针旋转，得到，则点C的坐标是（ ）

A．B．C．D．
二、填空题：本题共6小题，每小题3分，共18分．
11．的算术平方根是 ．
12．若是方程的根，则 ．
13．若且，则 ．
14．《周髀算经》中记载了“偃矩以望高”的方法．“矩”在古代指两条边呈直角的曲尺（即图中的）．“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度如图，点，，在同一水平线上，和均为直角，与相交于点．测得，则树高 m．

15．如图，和是以点为位似中心的位似图形．若，则与的周长比是 ．
16．如图，在正方形中，对角线与相交于点O，E为上一点，，F为的中点，若的周长为32，则的长为 ．

三、解答题：本题共9小题，共72分，解答应写出文字说明、证明过程或演算步骤．
17．计算：
18．先化简，再求值：，其中．
19．如图，在中，点E，F分别在，上，，．

(1)求证：四边形是矩形；
(2)，，，求的长．
20．建设美丽城市，改造老旧小区．某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同．
(1)求该市改造老旧小区投入资金的年平均增长率；
(2)2021年老旧小区改造的平均费用为每个80万元．2022年为提高老旧小区品质，每个小区改造费用增加15%．如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？
21．如图，，为的直径，为上一点，过点的切线与的延长线交于点，，点是的中点，弦，相交于点．
(1)求的度数；
(2)若，求直径的长．
22．如图，已知一次函数 的图象经过A（－2，－1）， B（1，3）两点，并且交x轴于点C，交y轴于点D．
(1)求该一次函数的解析式；
(2)求△AOB的面积．
23．如图，小文在数学综合实践活动中，利用所学的数学知识测量居民楼的高度，在居民楼前方有一斜坡，坡长，斜坡的倾斜角为，．小文在点处测得楼顶端的仰角为，在点处测得楼顶端的仰角为（点，，，在同一平面内）．
(1)求，两点的高度差；
(2)求居民楼的高度．（结果精确到，参考数据：）
24．为振兴乡村经济，在农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，某村委会统计了15名销售员在某月的销售额（单位：万元），数据如下：10，4，7，5，4，10，5，4，4，18，8，3，5，10，8
(1)补全月销售额数据的条形统计图．
(2)月销售额在哪个值的人数最多（众数）？中间的月销售额（中位数）是多少？平均月销售额（平均数）是多少？
(3)根据（2）中的结果，确定一个较高的销售目标给予奖励，你认为月销售额定为多少合适？
25．问题提出：如图（1），中，，是的中点，延长至点，使，延长交于点，探究的值．
(1)先将问题特殊化．如图（2），当时，直接写出的值；
(2)再探究一般情形．如图（1），证明（1）中的结论仍然成立．
问题拓展：如图（3），在中，，是的中点，是边上一点，，延长至点，使，延长交于点．直接写出的值（用含的式子表示）．
26．抛物线与x轴交于，两点，与y轴交于点C，直线y＝kx－6经过点B．点P在抛物线上，设点P的横坐标为m．
(1)求抛物线的表达式和t，k的值；
(2)如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；
(3)如图2，若点P在直线BC上方的抛物线上，过点P作PQ⊥BC，垂足为Q，求的最大值．
参考答案：
1．B
【分析】根据相反数的定义直接求解．
【详解】解：实数2022的相反数是，
故选：B．
【点睛】本题主要考查相反数的定义，解题的关键是熟练掌握相反数的定义．
2．A
【分析】根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
【详解】A．是轴对称图形，故A符合题意；
B．不是轴对称图形，故B不符合题意；
C．不是轴对称图形，故C不符合题意；
D．不是轴对称图形，故D不符合题意．
故选：A．
【点睛】本题主要考查轴对称图形的知识点．确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
3．C
【分析】利用方程有两个相等的实数根，得到=0，建立关于m的方程，解答即可．
【详解】∵一元二次方程有两个相等的实数根，
∴=0，
∴，
解得，故C正确．
故选：C．
【点睛】此题考查利用一元二次方程的根的情况求参数，一元二次方程的根有三种情况：有两个不等的实数根时>0；当一元二次方程有两个相等的实数根时，=0；当方程没有实数根时，<0，正确掌握此三种情况是正确解题的关键．
4．C
【分析】根据变量与常量的定义分别判断，并选择正确的选项即可．
【详解】解：2与π为常量，C与r为变量，
故选：C．
【点睛】本题考查变量与常量的概念，能够熟练掌握变量与常量的概念为解决本题的关键．
5．B
【分析】将方程组的两个方程相减，可得到，代入，即可解答．
【详解】解：，
得，
，
代入，可得，
解得，
故选：B．
【点睛】本题考查了根据解的情况求参数，熟练利用加减法整理代入是解题的关键．
6．C
【分析】根据平行四边形的性质：平行四边形的对边相等，然后对各选项进行判断即可．
【详解】解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC．
故选：C．
【点睛】本题考查了平行四边形的性质．解题的关键在于熟练掌握平行四边形的性质．
7．B
【分析】根据题意，先令在相同时间内走路快的人走100步，走路慢的人只走60步，从而得到走路快的人的速度，走路慢的人的速度，再根据题意设未知数，列方程即可
【详解】解：令在相同时间内走路快的人走100步，走路慢的人只走60步，从而得到走路快的人的速度，走路慢的人的速度，
设走路快的人要走x步才能追上，根据题意可得，
根据题意可列出的方程是，
故选：B．
【点睛】本题考查应用一元一次方程解决数学史问题，读懂题意，找准等量关系列方程是解决问题的关键．
8．B
【分析】过D作DE⊥AB垂足为E，先利用圆周角的性质和角平分线的性质得到DE=DC=1，再说明Rt△DEB≌Rt△DCB得到BE=BC，然后再利用勾股定理求得AE，设BE=BC=x，AB=AE+BE=x+，最后根据勾股定理列式求出x，进而求得AB．
【详解】解：如图：过D作DE⊥AB，垂足为E
∵AB是直径
∴∠ACB=90°
∵∠ABC的角平分线BD
∴DE=DC=1
在Rt△DEB和Rt△DCB中
DE=DC、BD=BD
∴Rt△DEB≌Rt△DCB（HL）
∴BE=BC
在Rt△ADE中，AD=AC-DC=3-1=2
AE=
设BE=BC=x，AB=AE+BE=x+
在Rt△ABC中，AB2=AC2+BC2
则（x+）2=32+x2，解得x=
∴AB=+=2
故填：2．
【点睛】本题主要考查了圆周角定理、角平分线的性质以及勾股定理等知识点，灵活应用相关知识成为解答本题的关键．
9．A
【分析】根据题意易证，根据证明方法即可求解．
【详解】解：O为、的中点，
，，
（对顶角相等），
在与中，
，
，
，
故选：A．
【点睛】本题考查了全等三角形的证明，正确使用全等三角形的证明方法是解题的关键．
10．B
【分析】过点作，由题意可得：，，再利用含30度直角三角形的性质，求解即可．
【详解】解：过点作，如下图：

则
由题意可得：，，
∴，
∴，
∴，，
∴点的坐标为，
故选：B
【点睛】此题考查了旋转的性质，坐标与图形，含30度直角三角形的性质，以及勾股定理，解题的关键是作辅助线，构造出直角三角形，熟练掌握相关基础性质．
11．2
【分析】根据算术平方根的运算法则，直接计算即可．
【详解】解：∵，4的算术平方根是2，
∴的算术平方根是2．
故答案为：2．
【点睛】此题考查了求一个数的算术平方根，这里需注意：的算术平方根和16的算术平方根是完全不一样的；因此求一个式子的平方根、立方根和算术平方根时，通常需先将式子化简，然后再去求，避免出错．
12．1
【分析】本题根据一元二次方程的根的定义，把x=1代入方程得到a的值．
【详解】把x=1代入方程，得1−2+a=0，
解得a=1，
故答案为：1．
【点睛】本题考查的是一元二次方程的根即方程的解的定义，一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．
13．
【分析】根据，利用完全平方公式可得，根据x的取值范围可得的值，利用平方差公式即可得答案．
【详解】∵，
∴，
∵，
∴，
∴=，
∴==，
故答案为：
【点睛】本题考查了完全平方公式及平方差公式，准确运用公式是解题的关键．
14．
【分析】根据题意可得，然后相似三角形的性质，即可求解．
【详解】解：∵和均为直角
∴，
∴，
∴
∵，
∴,
故答案为：．
【点睛】本题考查了相似三角形的应用，熟练掌握相似三角形的性质与判定是解题的关键．
15．
【分析】根据位似图形的性质，得到，根据得到相似比为，再结合三角形的周长比等于相似比即可得到结论．
【详解】解：和是以点为位似中心的位似图形，
，
，
，
，
根据与的周长比等于相似比可得，
故答案为：．
【点睛】本题考查相似图形的性质，掌握位似图形与相似图形的关系，熟记相似图形的性质是解决问题的关键．
16．
【分析】利用斜边上的中线等于斜边的一半和的周长，求出的长，进而求出的长，勾股定理求出的长，进而求出的长，利用三角形的中位线定理，即可得解．
【详解】解：的周长为32，
．
为DE的中点，
．
，
，
，
，
．
四边形是正方形，
，O为BD的中点，
是的中位线，
．
故答案为：．
【点睛】本题考查正方形的性质，斜边上的中线，三角形的中位线定理．熟练掌握斜边上的中线等于斜边的一半，是解题的关键．
17．4
【分析】根据零次幂、特殊角的正弦值、二次根式和去绝对值即可求解．
【详解】解：
．
【点睛】本题考查了实数的混合运算，掌握零次幂、特殊角的正弦值、二次根式的化简及去绝对值是解题的关键．
18．；
【分析】根据分式的混合运算法则把原式化简，把的值代入计算即可．
【详解】解：原式


，
当时，原式．
【点睛】本题考查的是分式的化简求值，掌握分式的混合运算法则是解题的关键．
19．(1)见解析
(2)
【分析】（1）利用平行四边形的性质求出，证明四边形是平行四边形，然后根据对角线相等的平行四边形是矩形得出结论；
（2）证明是等腰直角三角形，可得，然后再解直角三角形求出即可．
【详解】（1）证明：∵四边形是平行四边形，
∴，，
∵，
∴，
∴四边形是平行四边形，
∵，
∴平行四边形是矩形；
（2）解：由（1）知四边形是矩形，
∴，
∵，，
∴是等腰直角三角形，
∴，
又∵，
∴，
∴，
∴．
【点睛】本题考查了平行四边形的判定和性质，矩形的判定和性质以及解直角三角形，熟练掌握相关判定定理和性质定理是解题的关键．
20．(1)20%
(2)18个
【分析】（1）先设该市改造老旧小区投入资金的年平均增长率为，根据2019年投入资金2021年投入的总资金，列出方程求解即可；
（2）由（1）得出的资金年增长率求出2022年的投入资金，然后2022年改造老旧小区的总费用要小于等于2022年投入资金，列出不等式求解即可．
【详解】（1）解：设该市改造老旧小区投入资金的年平均增长率为，
根据题意得：，
解这个方程得，，，
经检验，符合本题要求．
答：该市改造老旧小区投入资金的年平均增长率为20%．
（2）设该市在2022年可以改造个老旧小区，
由题意得：，
解得．
∵为正整数，∴最多可以改造18个小区．
答：该市在2022年最多可以改造18个老旧小区．
【点睛】此题考查了一元二次方程的应用，不等式的应用，解决此题的关键是找到相应的等量关系和相应的不等关系，列出正确的方程和不等式．
21．(1)
(2)
【分析】（1）根据切线的性质，得出，再根据直角三角形两锐角互余，得出，再根据等边对等角，得出，再根据等量代换，得出，再根据，得出，即，得出，进而计算即可得出答案；
（2）连接，根据圆周角定理，得出，再根据中点的定义，得出，再根据同弧或同弦所对的圆周角相等，得出，再根据正切的定义，得出，再根据角所对的直角边等于斜边的一半，得出，进而即可得出答案．
【详解】（1）解：∵与相切于点，
∴，
∴，
∵，
∴，
∵，
∴，
∴，即，
∴，
∴；
（2）解：如图，连接，

∵是直径，
∴，
∵点是的中点，
∴，
∴，
在中，
∵，，
∴，
在中，
∵，
∴，
∴的直径的长为．
【点睛】本题考查了切线的性质、直角三角形两锐角互余、等边对等角、圆周角定理及其推论、锐角三角函数、含角的直角三角形的性质，解本题的关键在熟练掌握相关的性质定理．
22．(1)；
(2)
【分析】（1）先把A点和B点坐标代入y＝kx＋b得到关于k、b的方程组，解方程组得到k、b的值，从而得到一次函数的解析式；
（2）令y＝0，即可确定D点坐标，根据三角形面积公式和△AOB的面积＝S△AOD＋S△BOD进行计算即可．
【详解】（1）解：把A（－2，－1），B（1，3）代入y＝kx＋b，得
，
解得，
∴一次函数解析式为；
（2）解：把x＝0代入得，
所以D点坐标为（0，），
所以△AOB的面积＝S△AOD＋S△BOD．
【点睛】本题考查了待定系数法求一次函数解析式：①先设出函数的一般形式，如求一次函数的解析式时，先设y＝kx＋b；②将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；③解方程或方程组，求出待定系数的值，进而写出函数解析式．
23．(1)9m
(2)24m
【分析】（1）过点作，交的延长线于点，在中，可得，再利用勾股定理可求出，即可得出答案．
（2）过点作于，设，在中，，解得，在中，，，，求出的值，即可得出答案．
【详解】（1）解：过点作，交的延长线于点，
在中，，，
．
．
答：，两点的高度差为．
（2）过点作于，
由题意可得，，
设，
在中，，
解得，
在中，，，
，
解得，
．
答：居民楼的高度约为．
【点睛】本题考查解直角三角形的应用仰角俯角问题、坡度坡角问题，熟练掌握锐角三角函数的定义是解答本题的关键．
24．(1)作图见解析；
(2)月销售额在4万元的人数最多；中间的月销售额为5万元；平均数为7万元；
(3)月销售额定为7万元合适，
【分析】（1）根据所给数据确定销售额为4万元的人数为4人；销售额为8万元的人数为2人，然后补全条形统计图即可；
（2）根据众数、中位数及平均数的计算方法求解即可；
（3）根据题意，将月销售额定为7万元合适．
【详解】（1）解：根据数据可得：销售额为4万元的人数为4人；销售额为8万元的人数为2人；补全统计图如图所示：
（2）由条形统计图可得：月销售额在4万元的人数最多；
将数据按照从小到大排序后，中间的月销售额为第8名销售员的销售额为5万元；
平均数为：万元；
（3）月销售额定为7万元合适，给予奖励，可以激发销售员的积极性，振兴乡村经济．
【点睛】题目主要考查条形统计图及相关统计数据的计算方法，包括众数、中位数、平均数，以及利用平均数做决策等，理解题意，综合运用这些知识点是解题关键．
25．(1)[问题提出]（1）；（2）见解析
(2)[问题拓展]
【分析】[问题探究]（1）根据等边三角形的性质结合已知条件，求得，，根据含30度角的直角三角形的性质，可得，即可求解；
（2）取的中点，连接．证明，可得，根据，证明，根据相似三角形的性质可得，进而可得；
[问题拓展]方法同（2）证明，得出，，证明，得到，进而可得．
【详解】（1）[问题探究]：（1）如图，
中，，是的中点，，
是等边三角形，
，，
，
，
，
，
，
，
，
．
（2）证明：取的中点，连接．
∵是的中点，
∴，．
∵，
∴，
∴．
∵，
∴．
∴．
∴．
∴．
∴．
∵，
∴．
∴．
∴．
∴．
（2）[问题拓展]如图，取的中点，连接．
∵是的中点，
∴，．
∵，
∴，
∴．
∵，
∴．
∴．
∴．
∴．
，
∴．
∵，
∴．
∴．
∴．
∴．
．
【点睛】本题考查了等边三角形的性质，全等三角形的性质与判定，相似三角形的性质与判定，等边对等角，掌握相似三角形的性质与判定是解题的关键．
26．(1)，，t=3，
(2)点
(3)
【分析】（1）分别把代入抛物线解析式和一次函数的解析式，即可求解；
（2）作轴于点，根据题意可得，从而得到，，再根据，可求出m，即可求解；
（3）作轴交于点，过点作轴于点，则，再根据，可得，，然后根据，可得，从而得到，在根据二次函数的性质，即可求解．
【详解】（1）解：∵在抛物线上，
∴，
∴，
∴抛物线解析式为，
当时，，
∴，（舍），
∴．
∵在直线上，
∴，
∴，
∴一次函数解析式为．
（2）解：如图，作轴于点，
对于，令x=0，则y=-6，
∴点C（0，-6），即OC=6，
∵A（3，0），
∴OA=3，
∵点P的横坐标为m．
∴，
∴，，
∵∠CAP=90°，
∴，
∵，
∴，
∵∠AOC=∠AMP=90°，
∴，
∴，
∴，即，
∴（舍），，
∴，
∴点．
（3）解：如图，作轴交于点，过点作轴于点，
∵，
∴点，
∴，
∵PN⊥x轴，
∴PN∥y轴，
∴∠PNQ=∠OCB，
∵∠PQN=∠BOC=90°，
∴，
∴，
∵，，
∴，
∴，，
∵EN⊥y轴，
∴EN∥x轴，
∴，
∴，即
∴，
∴，
∴，
∴当时，的最大值是．
【点睛】本题主要考查了二次函数的综合题，熟练掌握二次函数的图象和性质，相似三角形的判定和性质，利用数形结合思想解答是解题的关键，是中考的压轴题．