2023-2024学年黑龙江省大庆市肇源县五校联考七年级（下）期中数学试卷（五四学制）（含解析）

这是一份2023-2024学年黑龙江省大庆市肇源县五校联考七年级（下）期中数学试卷（五四学制）（含解析），共18页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列计算正确的是( )
A. x2+x3=2x5B. x2⋅x3=x6C. x6÷x3=x3D. (−x3)2=−x6
2.下列语句叙述正确的有( )
①如果两个角有公共顶点且没有公共边，那么这两个角是对顶角；
②如果两个角相等，那么这两个角是对顶角；
③连接两点的线段的长度叫做两点间的距离；
④直线外一点到这条直线的垂线段叫做这点到直线的距离．
A. 0个B. 1个C. 2个D. 3个
3.下列各式中不能用平方差公式计算的是( )
A. (x−y)(−x+y)B. (−x+y)(−x−y)
C. (−x−y)(x−y)D. (x+y)(−x+y)
4.将一直角三角板与两边平行的纸条如图所示放置，有下列结论：
(1)∠1=∠2；(2)∠3=∠4；(3)∠2+∠4=90°；(4)∠4+∠5=180°．
其中正确的个数为( )
A. 1B. 2C. 3D. 4
5.如图，已知∠1=∠B，∠2=∠C，则下列结论不成立的是( )
A. ∠B=∠CB. AD//BCC. ∠2+∠B=180°D. AB/​/CD
6.下列正确说法的个数是( ) ①同位角相等；②等角的补角相等；③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直．
A. 1B. 2C. 3D. 4
7.弹簧挂上物体后会伸长，测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系：
那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
A. y=0.5x+12B. y=x+10.5C. y=0.5x+10D. y=x+12
8.如图，AB/​/CD，∠AGE=128°，HM平分∠EHD，则∠MHD的度数是( )
A. 46°
B. 23°
C. 26°
D. 24°
9.如图，从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0)，剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)，则矩形的面积为( )
A. (2a2+5a)cm2B. (6a+15)cm2C. (6a+9)cm2D. (3a+15)cm2
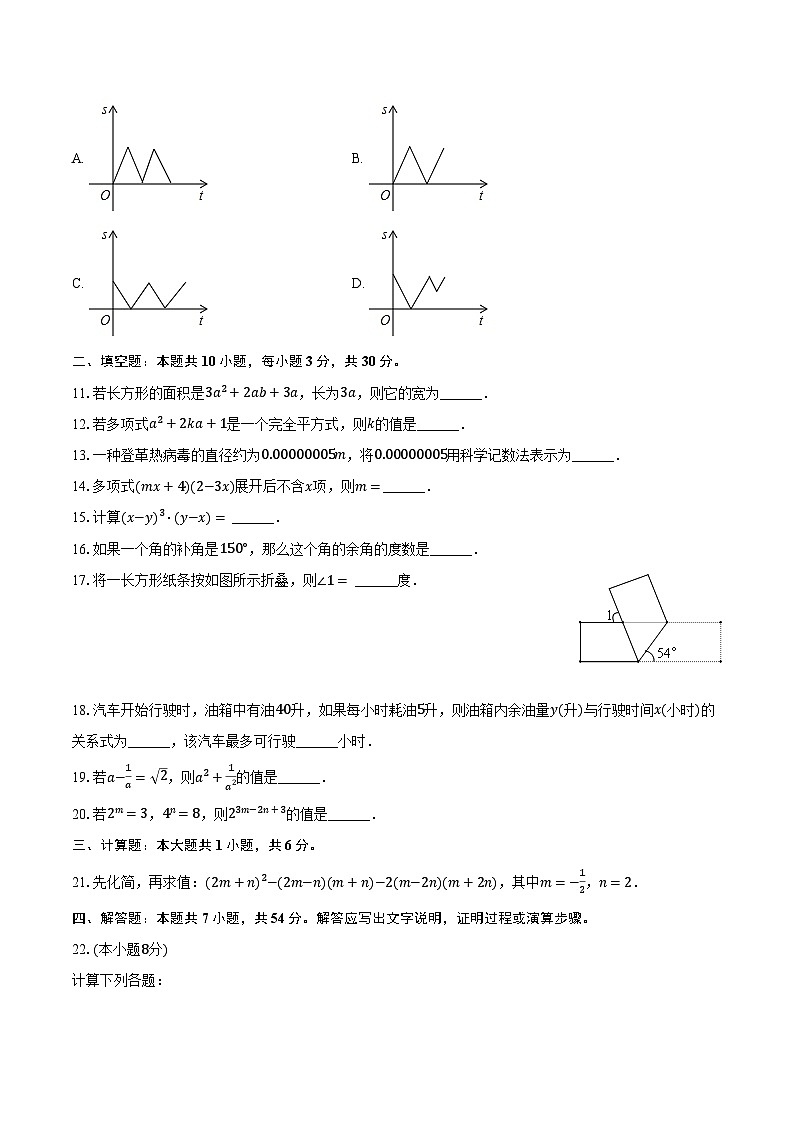
10.如图，在△ABC中，AC=BC，有一动点P从点A出发，沿A→C→B→A匀速运动．则CP的长度s与时间t之间的函数关系用图象描述大致是( )
A. B.
C. D.
二、填空题：本题共10小题，每小题3分，共30分。
11.若长方形的面积是3a2+2ab+3a，长为3a，则它的宽为______．
12.若多项式a2+2ka+1是一个完全平方式，则k的值是______．
13.一种登革热病毒的直径约为0.00000005m，将0.00000005用科学记数法表示为______．
14.多项式(mx+4)(2−3x)展开后不含x项，则m=______．
15.计算(x−y)3⋅(y−x)= ______．
16.如果一个角的补角是150°，那么这个角的余角的度数是______．
17.将一长方形纸条按如图所示折叠，则∠1= ______度．
18.汽车开始行驶时，油箱中有油40升，如果每小时耗油5升，则油箱内余油量y(升)与行驶时间x(小时)的关系式为______，该汽车最多可行驶______小时．
19.若a−1a= 2，则a2+1a2的值是______．
20.若2m=3，4n=8，则23m−2n+3的值是______．
三、计算题：本大题共1小题，共6分。
21.先化简，再求值：(2m+n)2−(2m−n)(m+n)−2(m−2n)(m+2n)，其中m=−12，n=2．
四、解答题：本题共7小题，共54分。解答应写出文字说明，证明过程或演算步骤。
22.(本小题8分)
计算下列各题：
(1)|−3|+(−1)2017×(π−3)0−(−12)−3；
(2)(2x+3y+5)(2x+3y−5)．
23.(本小题8分)
已知(a+b)2=5，(a−b)2=3，求下列式子的值：
(1)a2+b2；
(2)6ab．
24.(本小题6分)
如图，∠l=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3吗？说明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC(已知)
∴∠DEB=∠ABC=90° (______)
∴∠DEB+(______)=180°
∴DE/​/AB (______)
∴∠1=∠A(______)
∠2=∠3(______)
∵∠l=∠2(已知)
∴∠A=∠3(______)
25.(本小题7分)
如图，已知∠1=∠2，∠C=∠D，求证：∠A=∠F．
26.(本小题7分)
作图题.已知，∠α，∠β，且∠α大于∠β，求作∠AOB=∠α−∠β(不写作法，保留作图痕迹，不在原图上作图)
27.(本小题9分)
周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园．如图是他们离家路程s(km)与小明离家时间t(h)的关系图，请根据图回答下列问题：
(1)图中自变量是______，因变量是______；
(2)小明家到滨海公园的路程为______km，小明在中心书城逗留的时间为______h；
(3)小明出发______小时后爸爸驾车出发；
(4)图中A点表示______；
(5)小明从中心书城到滨海公园的平均速度为______km/h，小明爸爸驾车的平均速度为______km/h； (补充：爸爸驾车经过______追上小明；)
(6)小明从家到中心书城时，他离家路程s与坐车时间t之间的关系式为______．
28.(本小题9分)
如图1，点A、B在直线l1上，点C、D在直线l2上，AE平分∠BAC，CE平分∠ACD，∠EAC+∠ACE=90°．
(1)请判断l1与l2的位置关系并说明理由；
(2)如图2，在(1)的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系？请说明理由．
答案和解析
1.【答案】C
【解析】解：∵x2+x3不能合并，故选项A错误，
∵x2⋅x3=x5，故选项B错误，
∵x6÷x3=x3，故选项C正确，
∵(−x3)2=x6，故选项D错误，
故选：C．
根据各个选项中的式子可以计算出正确的结果，从而可以解答本题．
本题考查合并同类项、同底数幂的乘除法、幂的乘方，解答本题的关键是明确它们各自的计算方法．
2.【答案】B
【解析】解：①有公共顶点，且角的两边互为反向延长线的角是对顶角，说法错误；
②有公共顶点，且角的两边互为反向延长线的角是对顶角，错误；
③连接两点的线段的长度叫做两点间的距离，说法正确；
④直线外一点到这条直线的垂线段长度叫做这点到直线的距离，错误．
故选：B．
根据对顶角的定义以及性质、两点间的距离、点到直线的距离的定义对各选项分析判断后利用排除法求解．
本题主要考查了对顶角的定义以及对顶角相等的性质、两点间的距离、点到直线的距离的定义，是基础题，熟记概念与性质是解题的关键．
3.【答案】A
【解析】解：A、由于两个括号中含x、y项的符号都相反，故不能使用平方差公式，A正确；
B、两个括号中，−x相同，含y的项的符号相反，故能使用平方差公式，B错误；
C、两个括号中，含x项的符号相反，y项的符号相同，故能使用平方差公式，C错误；
D、两个括号中，含x项的符号相反，y项的符号相同，故能使用平方差公式，D错误；
故选：A．
根据公式(a+b)(a−b)=a2−b2的左边的形式，判断能否使用．
本题考查了平方差公式．注意两个括号中一项符号相同，一项符号相反才能使用平方差公式．
4.【答案】D
【解析】解：∵纸条的两边互相平行，
∴∠1=∠2，∠3=∠4，故(1)(2)正确；
∵三角板是直角三角板，
∴∠2+∠4=180°−90°=90°，故(3)正确；
∴∠3+∠5=180°，
∴∠4+∠5=180°，故(4)正确，
综上所述，正确的个数是4．
故选D．
根据平行线的性质，平角等于180°对各小题进行验证即可得解．
本题考查了平行线的性质，平角等于180°，邻补角的定义，熟记性质与概念并准确识图是解题的关键．
5.【答案】A
【解析】解：∵∠1=∠B，∠2=∠C，
而∠1+∠2=180°，
∴∠B+∠C=180°，所以A选项错误；
∵∠1=∠B，
∴AD//BC，所以B选项正确；
∴∠2+∠B=180°，所以C选项正确；
∵∠B+∠C=180°，
∴AB/​/DC，所以D选项正确；
故选：A．
先由∠1=∠B，∠2=∠C得到∠B+∠C=180°，然后根据平行线的判定与性质分别判断即可得到答案．
本题考查了平行线的判定与性质：同位角相等两直线平行；同旁内角互补两直线平行；两直线平行同旁内角互补．
6.【答案】B
【解析】【分析】
此题主要考查了等角的补角，平行线的性质，垂线的性质，关键是熟练掌握课本内容．
根据垂线的性质、平行线的性质、等角的补角对各小题分析判断后即可得解．
【解答】解：①两直线平行，同位角相等，错误；
②等角的补角相等，正确；
③两直线平行，同旁内角互补，错误；
④在同一平面内，过一点有且只有一条直线与已知直线垂直，正确．
故选B．
7.【答案】A
【解析】[分析]
由上表可知重物每增加1kg，弹簧伸长0.5cm，即可得出答案．
本题考查了列函数关系式，关键是找出表格中两个变量间的关系．
[解答]
解：
当x=1时，y=12+0.5，
当x=2时，y=12+2×0.5，
当x=3时，y=12+3×0.5，
所以，弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式为y=0.5x+12．
故选A．
8.【答案】C
【解析】【分析】
本题考查平行线的性质，关键在于掌握两直线平行，同位角相等，内错角相等，同旁内角互补．由题意可由平行线的性质，求出∠EHD的度数，再由HM平分∠EHD可求出∠2的度数．
【解答】
解：由题意得：∠BGH=∠AGE=128°，
∵AB/​/CD，
∴∠EHD=180°−∠BGH=52°，
又HM平分∠EHD，可得∠MHD=26°．
故选C．
9.【答案】B
【解析】解：矩形的面积是：(a+4)2−(a+1)2
=(a+4+a+1)(a+4−a−1)
=3(2a+5)
=6a+15(cm2).
故选：B．
大正方形与小正方形的面积的差就是矩形的面积，据此即可求解．
本题考查了平方差公式的几何背景，理解大正方形与小正方形的面积的差就是矩形的面积是关键．
10.【答案】D
【解析】【分析】
本题考查了动点问题的函数图象．用图象解决问题时，要理清图象的含义即会识图．
分类讨论：点P在边AC上时，s随t的增大而减小；当点P在边BC上时，s随t的增大而增大；当点P在线段BD上时，s随t的增大而减小；当点P在线段AD上时，s随t的增大而增大．
【解答】
解：如图，过点C作CD⊥AB于点D．
因为在△ABC中，AC=BC，
所以AD=BD．
①点P在边AC上时，s随t的增大而减小．故A、B错误；
②当点P在边BC上时，s随t的增大而增大；
③当点P在线段BD上时，s随t的增大而减小，点P与点D重合时，s时点P在线段BD上的最小值，但是不等于零．故C错误；
④当点P在线段AD上时，s随t的增大而增大．故D正确．
故选：D．
11.【答案】a+23b+1
【解析】解：根据题意得：(3a2+2ab+3a)÷(3a)=a+23b+1，
故答案为：a+23b+1
根据长方形的面积除以长确定出宽即可．
此题考查了整式的除法，熟练掌握除法法则是解本题的关键．
12.【答案】±1
【解析】解：∵a2+2ka+1是一个完全平方式，
∴2ka=±2a⋅1，
解得：k=±1，
故答案为：±1．
完全平方公式有两个：a2+2ab+b2和a2−2ab+b2，根据以上公式得出2ka=±2a⋅1，求出即可．
本题考查了完全平方公式，关键在于熟记公式，理解完全平方公式的特点．
13.【答案】5×10−8
【解析】解：0.00000005=5×10−8．
故答案为：5×10−8．
科学记数法表示形式为a×10n(1≤|a|<10)，数出5前边0的个数确定10的指数，而指数恰好是这个数的相反数，据此即可写出本题．
本题考查了科学记数法，关键是熟练掌握科学记数法的定义．
14.【答案】6
【解析】解：∵(mx+4)(2−3x)
=2mx−3mx2+8−12x
=−3mx2+(2m−12)x+8
∵展开后不含x项
∴2m−12=0
即m=6
故填空答案：6．
先将多项式展开，再合并同类项，然后根据题意即可解答．
此题展开后必须先合并同类项，否则容易误解为m=0．
15.【答案】−(x−y)4
【解析】解：(x−y)3⋅(y−x)=−(x−y)3⋅(x−y)=−(x−y)3+1=−(x−y)4．
故答案为：−(x−y)4．
根据同底数幂的乘法法则计算即可．同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．
本题考查了同底数幂的乘法，掌握幂的运算法则是解答本题的关键．
16.【答案】60°
【解析】解：∵一个角的补角是150°，
∴这个角是180°−150°=30°，
∴这个角的余角是90°−30°=60°．
故答案是：60°．
首先根据补角的定义求得这个角的度数，然后根据余角的定义即可求出这个角的余角．
此题主要考查的是补角和余角的定义，属于基础题，较简单，主要记住互为余角的两个角的和为90°；互为补角的两个角的和为180°．
17.【答案】72
【解析】解：∵矩形EFGH，
∴EH/​/FG，
∴∠HAB+∠ABG=180°，
∵沿BD折叠BG和BA所在直线重合，
∴∠ABG=2∠DBC=2×54°=108°，
∴∠HAB=180°−108°=72°，
∴∠1=∠HAB=72°，
故答案为：72．
根据矩形的性质得到EH/​/FG，根据平行线的性质得到∠HAB+∠ABG=180，求出∠ABG的度数，进一步求出∠HAB的度数，根据对顶角相等即可求出答案．
本题主要考查对对顶角的性质，矩形的性质，平行线的性质，翻折变换等知识点的理解和掌握，能熟练地运用这些性质进行计算是解此题的关键．
18.【答案】y=40−5x 8
【解析】解：依题意得，油箱内余油量y(升)与行驶时间x(小时)的关系式为：y=40−5x，
当y=0时，40−5x=0，
解得：x=8，
即汽车最多可行驶8小时．
故答案为：y=40−5x，8．
根据：油箱内余油量=原有的油量−x小时消耗的油量，可列出函数关系式，进而得出行驶的最大路程．
本题考查了列函数关系式以及代数式求值．关键是明确油箱内余油量，原有的油量，x小时消耗的油量，三者之间的数量关系，根据数量关系可列出函数关系式．
19.【答案】4
【解析】解：∵a−1a= 2，
∴(a−1a)2=2，即a2−2+1a2=2，
∴a2+1a2=4，
故答案为：4．
将已知等式两边平方可得a2−2+1a2=2，据此可得答案．
本题主要考查分式的化简求值，解题的关键是掌握完全平方公式．
20.【答案】27
【解析】解：因为2m=3，4n=8，
所以23m−2n+3=(2m)3÷(22)n×23，
=(2m)3÷4n×23，
=33÷8×8，
=27．
故答案为：27．
根据同底数幂的乘除法，幂的乘方的性质的逆运用先表示成已知条件的形式，然后代入数据计算即可．
本题考查了同底数幂的乘除法，幂的乘方的性质，逆用运算性质，将23m−2n+3化为(2m)3÷(22)n×23是求值的关键，逆用幂的运算法则巧求代数式的值是中考的重要题型，由此可见，我们既要熟练地正向使用法则，又要熟练地逆向使用法则．
21.【答案】解：原式=(4m2+4mn+n2)−(2m2+2mn−mn−n2)−2(m2−4n2)
=4m2+4mn+n2−2m2−2mn+mn+n2−2m2+8n2
=3mn+10n2，
当m=−12，n=2时，原式=−3+40=37．
【解析】原式利用完全平方公式，平方差公式，以及多项式乘以多项式法则计算，去括号合并得到最简结果，把m与n的值代入计算即可求出值．
此题考查了整式的混合运算−化简求值，熟练掌握运算法则是解本题的关键．
22.【答案】解：(1)|−3|+(−1)2017×(π−3)0−(−12)−3
=3+(−1)×1−(−8)
=3−1+8
=2+8
=10；
(2)(2x+3y+5)(2x+3y−5)
=[(2x+3y)+5)][(2x+3y)−5]
=(2x+3y)2−52
=4x2+12xy+9y2−25．
【解析】(1)分别根据绝对值的性质，有理数的乘方的定义，零指数幂的定义以及负整数指数幂的定义计算即可；
(2)根据平方差公式和完全平方公式化简即可．
本题考查了实数的运算以及整式的混合运算，掌握相关公式与定义是解答本题的关键．
23.【答案】解：(1)∵(a+b)2=5，(a−b)2=3，
∴a2+2ab+b2=5，a2−2ab+b2=3，
∴2(a2+b2)=8，
解得：a2+b2=4；
(2)∵a2+b2=4，
∴4+2ab=5，
解得：ab=12，
∴6ab=3．
【解析】(1)直接利用完全平方公式将原式展开，进而求出a2+b2的值；
(2)直接利用(1)中所求，进而得出ab的值，求出答案即可．
此题主要考查了完全平方公式，正确应用完全平方公式是解题关键．
24.【答案】垂直的定义；∠ABC；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；等量代换
【解析】【分析】
本题考查了平行线的判定与性质：平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．先根据垂直定义得到∠DEC=∠ABC=90°，则利用平行线的判定可得DE/​/AB，然后根据平行线得性质得到∠2=∠3，∠1=∠A，再利用等量代换可得∠A=∠3．
【解答】
解：理由如下：
∵DE⊥BC，AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直的定义)，
∴∠DEB+(∠ABC)=180O
∴DE//AB(同旁内角互补相等，两直线平行)，
∴∠1=∠A (两直线平行，同位角相等)，
由DE/​/BC还可得到：
∠2=∠3 (两直线平行，内错角相等)，
又∵∠l=∠2(已知)
∴∠A=∠3 (等量代换)．
故答案为垂直的定义；∠ABC；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；等量代换．
25.【答案】证明：∵∠1=∠2，
∴BD/​/CE，
∴∠C+∠CBD=180°，
∵∠C=∠D，
∴∠D+∠CBD=180°，
∴AC/​/DF，
∴∠A=∠F．
【解析】根据平行线判定推出BD/​/CE，求出∠D+∠CBD=180°，推出AC/​/DF，根据平行线性质推出即可．
本题考查了平行线性质和判定的应用，主要考查学生的推理能力．
26.【答案】解：如图∠AOB即为所求．

【解析】如图在射线OC的同侧作∠AOC=α，∠BOC=β即可解决问题．
本题考查作图−基本作图，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
27.【答案】(1)t ，s；
(2)30 ，1.7 ；
(3)2.5 ；
(4) 2.5小时后小明继续坐公交车到滨海公园 ；
(5)12 ，30， 23h；
(6) s=15t(0≤t≤0.8)
【解析】解：(1)由图可得，自变量是t，因变量是s，
故答案为：t，s；
(2)由图可得，小明家到滨海公园的路程为30km，小明在中心书城逗留的时间为2.5−0.8=1.7(h)；
故答案为：30，1.7；
(3)由图可得，小明出发2.5小时后爸爸驾车出发；
故答案为：2.5；
(4)由图可得，A点表示2.5小时后小明继续坐公交车到滨海公园；
故答案为：2.5小时后小明继续坐公交车到滨海公园；
(5)小明从中心书城到滨海公园的平均速度为30−124−2.5=12(km/h)，
小明爸爸驾车的平均速度为303.5−2.5=30(km/h)；
爸爸驾车经过1230−12=23h追上小明；
故答案为：12，30，23h；
(6)小明从家到中心书城时，他的速度为120.8=15(km/h)，
所以他离家路程s与坐车时间t之间的关系式为s=15t(0≤t≤0.8)，
故答案为：s=15t(0≤t≤0.8)．
(1)根据图象进行判断，即可得出自变量与因变量；
(2)根据图象中数据进行计算，即可得到路程与时间；
(3)根据梯形即可得到爸爸驾车出发的时间；
(4)根据点A的坐标即可得到点A的实际意义；
(5)根据相应的路程除以时间，即可得出速度；
(6)根据小明从家到中心书城时的速度，即可得到离家路程s与坐车时间t之间的关系式．
本题主要考查了函数图象，以及行程问题的数量关系的运用，解答时理解清楚函数图象的意义是解答此题的关键．
28.【答案】解：(1)如图1中，
∵AE平分∠BAC，CE平分∠ACD(已知)，
∴∠BAC=2∠1，∠ACD=2∠2(角平分线的定义)，
又∵∠1+∠2=90°(已知)，
∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°(等量代换)，
∴l1/​/l2(同旁内角互补，两直线平行)．
(2)①如图2中，当Q在C点左侧时，过点P作PE//l1，
∵l1//l2(已证)，
∴PE//l2(同平行于一条直线的两直线互相平行)，
∴∠1=∠2，(两直线平行，内错角相等)，
∠BAC=∠EPC，(两直线平行，同位角相等)，
又∵∠EPC=∠1+∠CPQ，
∴∠BAC=∠CQP+∠CPQ(等量代换)．
②如图3中，当Q在C点右侧时，过点P作PE//l1，
∵l1//l2(已证)，
∴PE//l2(同平行于一条直线的两直线互相平行)，
∴∠1=∠2，∠BAC=∠APE，(两直线平行，内错角相等)，
又∵∠EPC=∠1+∠CPQ，
∵∠APE+∠EPC=180°(平角定义)，
∴∠CPQ+∠CQP+∠BAC=180°．
【解析】(1)想办法证明∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°即可；
(2)分点Q在C点左侧、点Q在C点右侧两种情形分别求解即可解决问题；
本题考查平行线的判定和性质等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．x(kg)
0
1
2
3
4
5
6
y(cm)
12
12.5
13
13.5
14
14.5
15