十年（2014-2023）高考数学真题分项汇编（全国通用）专题13 算法初步（理科）

这是一份十年（2014-2023）高考数学真题分项汇编（全国通用）专题13 算法初步（理科），共31页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

题型一：程序框图中的数列求解问题
题型二：程序框图中的函数求值问题
题型三：程序框图在解决其他问题中的应用
题型四：算法案例
题型五：算法语句
题型一：程序框图中的数列求解问题
一、选择题
（2019·全国Ⅲ·理·第9题）
执行如图所示的程序框图，如果输入的为，则输出的值等于
（2018年高考数学课标Ⅱ卷（理）·第7题）
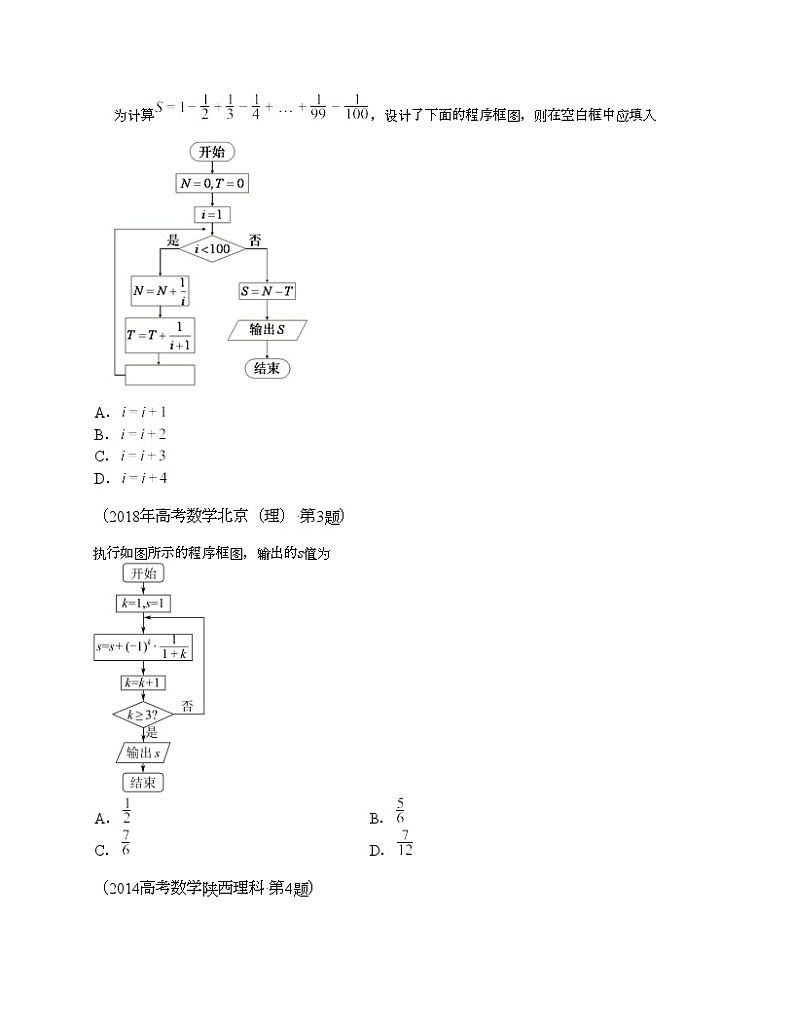
为计算，设计了下面的程序框图，则在空白框中应填入
（2018年高考数学北京（理）·第3题）
执行如图所示的程序框图，输出的s值为

（2014高考数学陕西理科·第4题）
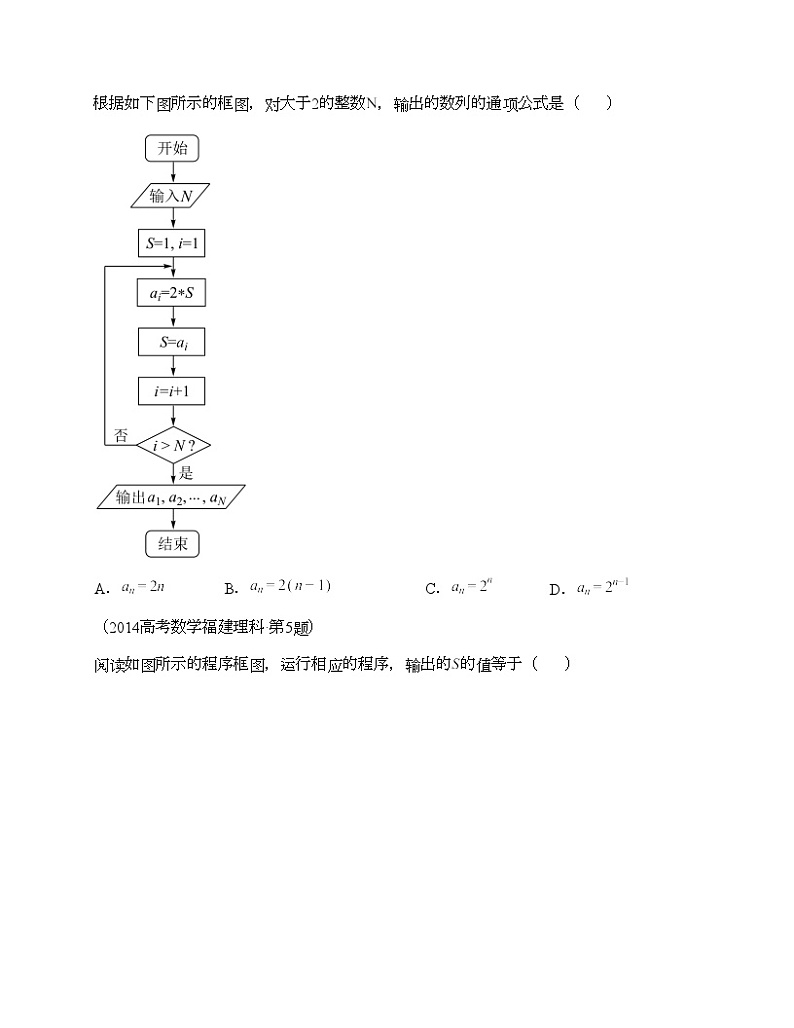
根据如下图所示的框图，对大于2的整数，输出的数列的通项公式是（ ）
（2014高考数学福建理科·第5题）
阅读如图所示的程序框图，运行相应的程序，输出的的值等于（ ）
（2015高考数学湖南理科·第3题）
执行如图所示的程序框图，如果输入n=3，输出的S=
（2015高考数学福建理科·第6题）
阅读如图所示的程序框图，运行相应的程序，则输出的结果为
（2017年高考数学课标Ⅲ卷理科·第7题）
执行下面的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为
（2017年高考数学课标Ⅱ卷理科·第8题）
执行如图所示的程序框图，如果输入的，则输出的
（2017年高考数学北京理科·第3题）
执行如图所示的程序框图,输出的s值为( )
（2014高考数学浙江理科·第11题）
若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.

（2015高考数学安徽理科·第13题）
执行如图所示的程序框图(算法流程图)，输出的n为________．
题型二：程序框图中的函数求值问题
（2019·天津·理·第4题）
阅读下边的程序框图，运行相应的程序，输出的值为
（2014高考数学重庆理科·第5题）
执行如题图所示的程序框图，若输出的值为6，则判断框内可填入的条件是
（2014高考数学天津理科·第3题）
阅读下面的程序框图，运行相应的程序，输出S的值为( )

（2014高考数学四川理科·第5题）
执行如图的程序框图，如果输入的，那么输出的S的最大值为（ ）．
（2014高考数学课标2理科·第7题）
执行右图程序框图，如果输入的x,t均为2，则输出的S=
（2014高考数学课标1理科·第7题）
执行右面的程序框图，若输入的分别为1,2,3，则输出的
（2014高考数学江西理科·第7题）
阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为
（2014高考数学湖南理科·第6题）
执行如图所示的程序框图，如果输入的，则输出的属于
（2014高考数学北京理科·第4题）
当时,执行如图所示的程序框图，输出的S值为( )
（2014高考数学安徽理科·第3题）
如图所示，程序框图（算法流程图）的输出结果是
（2015高考数学重庆理科·第7题）
执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是( )
（2015高考数学新课标1理科·第9题）
执行下面的程序框图，如果输入的，则输出的
（2015高考数学四川理科·第3题）
执行如图所示的程序框图，输出S的值是
（2015高考数学陕西理科·第8题）
根据右边的图，当输入为时，输出的（ ）
二、填空题
（2020江苏高考·第5题）
如图是一个算法流程图，若输出的值为，则输入的值是_____.
（2017年高考数学江苏文理科·第4题）
如图是一个算法流程图，若输入x的值为，则输出y的值是____.
（2014高考数学辽宁理科·第13题）
执行右侧的程序框图，若输入，则输出 .
题型三：程序框图在解决其他问题中的应用
（2023年全国甲卷理科·第3题）
执行下面的程序框图，输出的（ ）

（2022年高考全国乙卷数学（理）·第6题）
执行下边的程序框图，输出的（ ）
（2019·北京·理·第2题）
执行如图所示的程序框图，输出的s值为
（2018年高考数学天津（理）·第3题）
阅读如图所示的程序框图，运行相应的程序，若输入的值为20，则输出的值为
（2014高考数学江苏·第3题）
如图是一个算法流程图，则输出的n的值是_____________.
（2015高考数学山东理科·第13题）
执行右边的程序框图，输出的的值为_____________.
（2015高考数学北京理科·第3题）
执行如图所示的程序框图，输出的结果为（ ）
（2017年高考数学新课标Ⅰ卷理科·第8题）
如图是为了求出满足的最小偶数，那么在和两个空白框中，可以分别填入

（2017年高考数学天津理科·第3题）
阅读下面的程序框图，运行相应的程序，若输入的值为24，则输出的值为
（2017年高考数学山东理科·第6题）
执行两次下图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
（2015高考数学天津理科·第3题）
阅读如图所示的程序框图,运行相应的程序,则输出S的值为( )
（2016高考数学天津理科·第4题）
阅读下边的程序框图，运行相应的程序，则输出S的值为
（2016高考数学课标Ⅲ卷理科·第7题）
执行下面的程序框图，如果输入的a=4，b=6，那么输出的n=
（2016高考数学课标Ⅰ卷理科·第9题）
执行如图的程序框图，如果输入的，则输出的值满足
（2016高考数学北京理科·第3题）
执行如图所示的程序框图，若输入的a值为1，则输出的k值为
（2019·江苏·第3题）
如图是一个算法流程图，则输出的S的值是______________.
（2014高考数学山东理科·第11题）
执行如图所示的程序框图，若输入的的值为1，则输出的的值为 .
（2014高考数学湖北理科·第13题）
设是一个各位数字都不是0且没有重复数字的三位数.将组成的3个数字按从小到大排成的三位数记为，按从大到小排成的三位数记为（例如，则，）.阅读如图所示的程序框图，运行相应的程序，任意输入一个，输出的结果__________.
（2016高考数学山东理科·第11题）
执行下面的程序框图，若输入的a，b的值分别为0和9，则输出的i的值为____.
（2016高考数学江苏文理科·第6题）
如图是一个算法的流程图，则输出的a的值是___________．
题型四：算法案例
（2015高考数学新课标2理科·第8题）
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入分别为14,18，则输出的（ ）
（2016高考数学四川理科·第6题）
秦九昭是我国南宋时期的数学家，普州（现在四川安岳人），他在所著的《数书九章》中提出的多项式求值的秦九昭算法，至今仍是比较先进的算法，如图所示的程序给出了利用秦九昭算法求多项式值的一个实例.如输入的值分别是，则输出的的值为（ ）
（2016高考数学课标Ⅱ卷理科·第8题）
中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的，，依次输入的为2，2，5，则输出的
题型五：算法语句
（2018年高考数学江苏卷·第4题）
一个算法的伪代码如图所示，执行此算法，最后输出的S的值为________．
（2015高考数学江苏文理·第4题）
根据如图所示的伪代码，可知输出的结果S为________.
A．
B．
C．
D．
A．
B．
C．
D．
A．
B．
C．
D．
A．
B．
C．
D．
A．18
B．20
C．21
D．40
A．
B．
C．
D．
A．2
B．1
C．0
D．
A．5
B．4
C．3
D．2
A．2
B．3
C．4
D．5
A．2
B．
C．
D．
A．5
B．8
C．24
D．29
A．
B．
C．
D．
A．15
B．105
C．245
D．945
A．0
B．1
C．2
D．3
A．4
B．5
C．6
D．7
A．
B．
C．
D．
A．7
B．9
C．10
D．11
A．
B．
C．
D．
A．7
B．42
C．210
D．840
A．34
B．55
C．78
D．89
A．s≤?
B．s≤?
C．s≤?
D．s≤?
A．
B．
C．
D．
A．
B．
C．
D．
A．28
B．10
C．4
D．2
A．21
B．34
C．55
D．89
A．3
B．4
C．5
D．6
A．1
B．2
C．3
D．4
A．1
B．2
C．3
D．4
A．
B．
C．
D．
A．和
B．和
C．和
D．和
A．0
B．1
C．2
D．3
A．0,0
B．1,1
C．0,1
D．1,0
A．-10
B．6
C．14
D．18
A．2
B．4
C．6
D．8
A．3
B．4
C．5
D．6
A．
B．
C．
D．
A．1
B．2
C．3
D．4
A．0
B．2
C．4
D．14
A．
B．
C．
D．
A．7
B．12
C．17
D．34