山东省枣庄市峄城区2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份山东省枣庄市峄城区2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含山东省枣庄市峄城区2023-2024学年七年级下学期期中数学试题原卷版docx、山东省枣庄市峄城区2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

1．本试卷共6页，满分120分，考试用时120分钟．
2．答卷前，考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上．
3．选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试题卷上．
4．非选择题必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．
一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是正确的．
1. 下列计算结果正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题考查了同底数幂的除法，同底数幂的乘法，合并同类项，积的乘方，熟记法则并根据法则计算是解题关键．
根据合并同类项系数相加字母及指数不变，同底数幂的除法底数不变指数相减，同底数幂的乘法底数不变指数相加，积的乘方等于乘方的积，可得答案．
【详解】解：A． 不能合并，故选项错误，不合题意，
B． ，故选项错误，不合题意，
C． 故选项正确，符合题意，
D． ，故选项错误，不合题意．
故选：C．
2. 若，，则的值为（ ）
A. -6B. C. 10D. 16
【答案】B
【解析】
【分析】根据同底数幂的除法运算法则进行计算即可．
【详解】∵，，
∴，
故选：B．
【点睛】本题考查了同底数幂的除法，掌握同底数幂的除法的逆运算是解题的关键．
3. 如图，下列条件： ①∠DCA=∠CAF，②∠C =∠EDB，③∠BAC+∠C=180°，④∠GDE +∠B=180°．其中能判断AB∥CD的是（ ）
A. ①④B. ②③④C. ①③④D. ①②③
【答案】C
【解析】
【分析】利用平行线的判定方法分别判断即可得出答案．
【详解】解：①当∠DCA=∠CAF时，AB∥CD，符合题意；
②当∠C=∠EDB时，AC∥DB，不合题意；
③当∠BAC+∠C=180°时，AB∥CD，符合题意；
④当∠GDE+∠B=180°时，
又∵∠GDE+∠EDB=180°，
∴∠B=∠EDB，
∴AB∥CD，符合题意；
故选：C．
【点睛】本题考查的是平行线的判定，内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补，两直线平行，正确掌握平行线的判定是解题关键．．
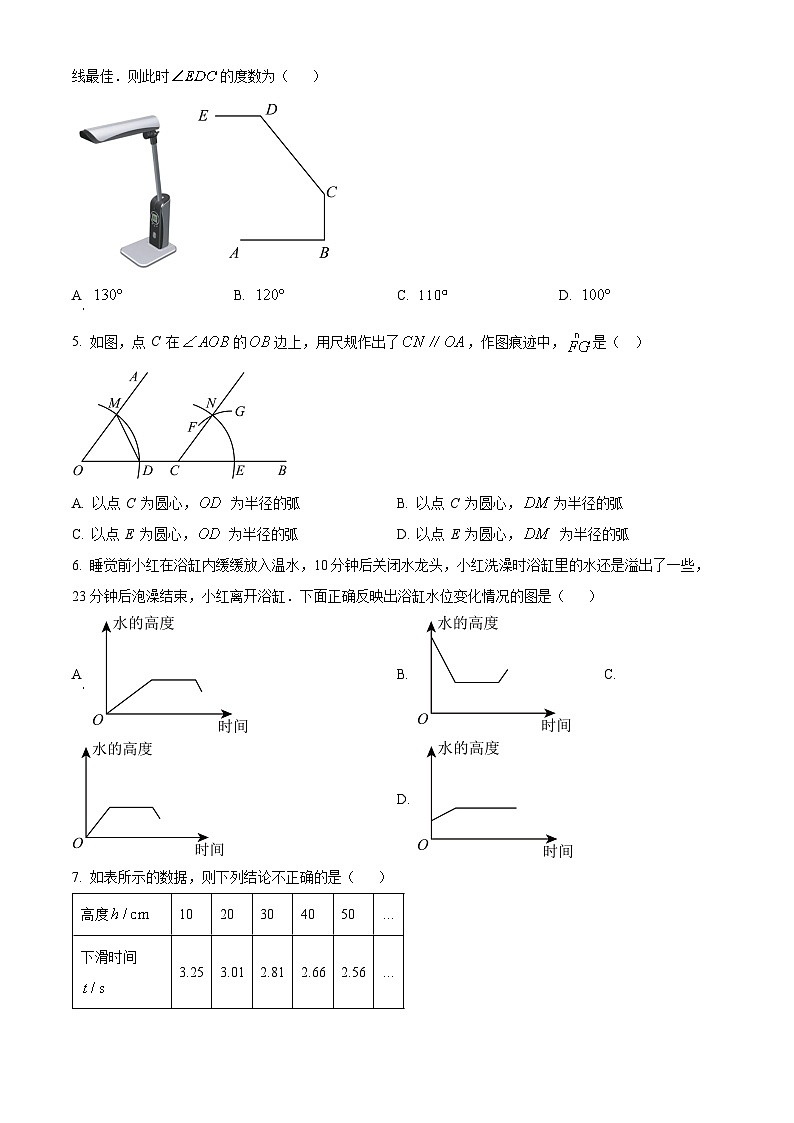
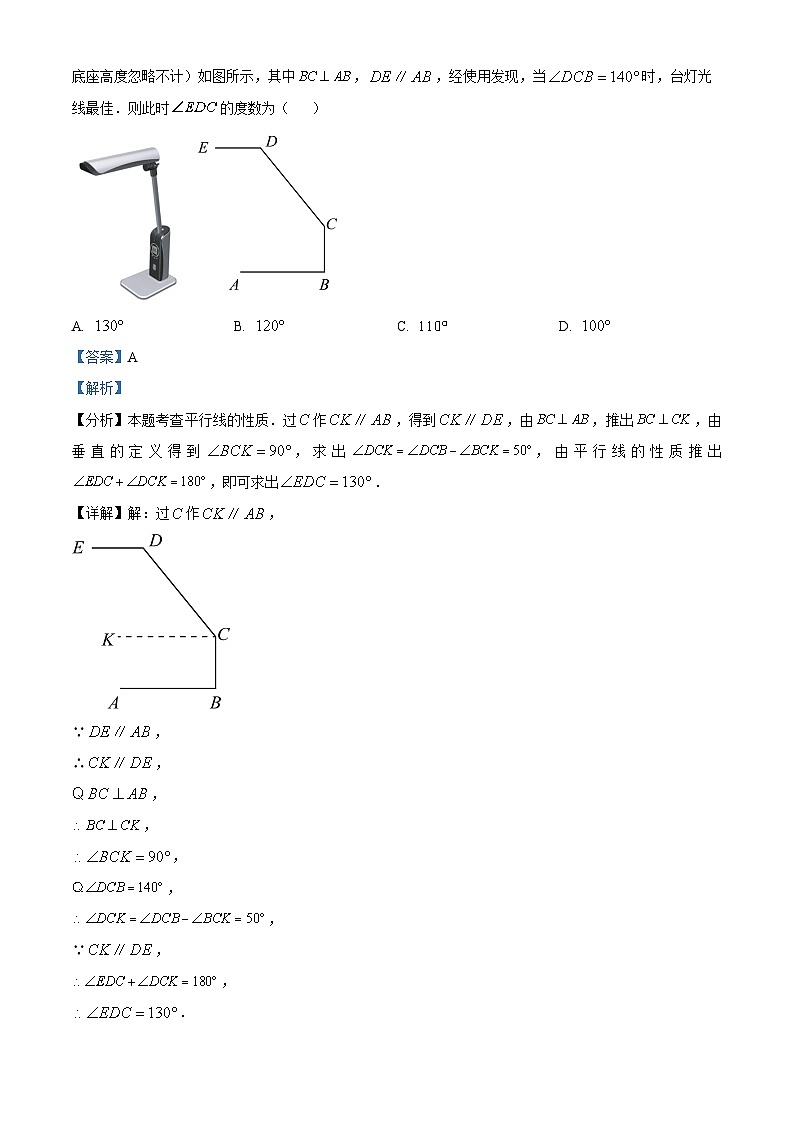
4. 近几年中学生近视的现象越来越严重，为响应国家的号召，某公司推出了护眼灯，其侧面示意图（台灯底座高度忽略不计）如图所示，其中，，经使用发现，当时，台灯光线最佳．则此时的度数为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查平行线的性质．过作，得到，由，推出，由垂直的定义得到，求出，由平行线的性质推出，即可求出．
【详解】解：过作，
∵，
∴，
，
，
，
，
，
∵，
，
．
故选：A．
5. 如图，点 C 在的边上，用尺规作出了，作图痕迹中，是（ ）
A. 以点 C 为圆心， 为半径的弧B. 以点 C 为圆心，为半径的弧
C. 以点 E 为圆心， 为半径的弧D. 以点 E 为圆心， 为半径的弧
【答案】D
【解析】
【分析】本题主要考查作图-尺规作图，解题的关键是熟练掌握作一个角等于已知角的尺规作图步骤．根据作一个角等于已知角的步骤即可得．
【详解】解：作图痕迹中，是以点 E 为圆心， 为半径的弧．
故选：D．
6. 睡觉前小红在浴缸内缓缓放入温水，10分钟后关闭水龙头，小红洗澡时浴缸里的水还是溢出了一些，23分钟后泡澡结束，小红离开浴缸．下面正确反映出浴缸水位变化情况的图是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据分钟，浴缸水位上升，分钟，浴缸水位保持不变，分钟后，水位略下降，进行判断作答即可．
【详解】解：由题意知，分钟，浴缸水位上升，分钟，浴缸水位保持不变，分钟后，水位略下降，
故选：C．
【点睛】本题考查了用图象表示变量间的关系．解题的关键在于理解题意．
7. 如表所示的数据，则下列结论不正确的是（ ）
A. 在这个变化中，高度是自变量
B. 随着高度的增加，下滑时间越来越短
C. 当时，t约为
D 高度每增加，下滑时间就减少
【答案】D
【解析】
【分析】本题主要考查了函数的表示方法，依据表格反映的规律回答问题是解题的关键．依据题意，根据列表法表示的函数，通过表格反映的规律，对每一个选项进行验证可以得解．
【详解】解：根据表格可知，高度是自变量，下滑时间是因变量，
选项正确，不符合题意．
从表中数据看到：当由10逐渐增大到50时，的值由3.25逐渐减小到2.56，
随高度增加，下滑时间越来越短．
B选项正确，不符合题意．
从表中的对应值可以看到当时，，
C选项正确，不符合题意．
因为时间的减少是不均匀的，
选项错误，符合题意．
综上，只有选项错误．
故选：D．
8. 在中，是边上的高的图形是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了三角形的高；
从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高，据此判断即可．
【详解】解：A.不是边上的高，不符合题意；
B.不是边上的高，不符合题意；
C.不是边上的高，不符合题意；
D.是边上的高，符合题意；
故选：D．
9. 下列各组图形中，不是全等图形的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查的是全等形的识别．根据能够完全重合的两个图形是全等图形对各选项分析即可得解．
【详解】解：观察发现，B、C、D选项的两个图形都可以完全重合，
∴B、C、D选项的两个图形都是全等图形，
A选项中两个图形不可能完全重合，
∴它们不是全等形．
故选：A．
10. 一个三角形的两边长分别为2和6，则第三边长可能是（ ）
A. 1B. 3C. 4D. 6
【答案】D
【解析】
【分析】本题考查三角形三边关系定理，掌握两边之和大于三边，两边之差小于第三边，属于基础题．根据三角形三边关系，两边之和大于第三边，两边之差小于第三边即可判断．
【详解】解：设第三边为x，则，
∴
所以第三边长可能是6．
故选：D．
二、填空题：本题共6小题，每小题填对得3分，共18分．只要求在答题纸上填写最后结果．
11. 华为于2023年8月29日开售，该款手机搭载的是华为自主研发的麒麟9000s芯片，该款芯片达到了7纳米工艺水平，1纳米米，7纳米用科学计数法表示为：______米．
【答案】
【解析】
【分析】本题主要考查了科学记数法，科学记数法的表现形式为的形式，其中，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正数，当原数绝对值小于1时n是负数；由此进行求解即可得到答案．
【详解】解：7纳米米，
故答案为：．
12. 古希腊一位庄园主把一边长为a米（）的正方形土地租给老农，第二年他对老农说：“我把这块地的一边增加4米，相邻的一边减少4米，变成长方形土地继续租给你，租金不变”后来老农发现收益减少，感觉吃亏了．聪明的你帮老农算出土地面积其实减少了__________平方米．
【答案】16
【解析】
【分析】本题主要平方差公式与几何图形的知识，正确理解题意列出代数式并计算是解题的关键．
分别求出变化前后2次的面积，作差即可．
【详解】原来的土地面积为平方米，第二年的面积为，
∵，
∴减少了16平方米，
故答案为：16．
13. 如图，，，垂足为．若，则_______．
【答案】40°
【解析】
【分析】∠1和∠2是对顶角相等，∠2和∠3为同位角，根据两直线平行，同位角相等可求出∠3，在直角三角形中，两锐角互余，即可求解．
【详解】解：∵∠1=50°，
∴∠1=∠2（对顶角相等），
∵AB∥CD，
∴∠3=∠2=50°，
又∵EG⊥AB，
∴∠E=90°-∠3=90°-∠50°=40°．
故答案为：40°．
【点睛】本题主要考查了平行线的性质以及直角三角形两锐角互余的关系，熟练掌握性质定理是解题的关键．
14. 如图，木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住，∠EGB＝100°，∠EHD＝80°，将木棒AB绕点G逆时针旋转到与木棒CD平行的位置，则至少要旋转 ___°．
【答案】20
【解析】
【分析】根据同位角相等两直线平行，得出当∠EHD＝∠EGN=80°，MN//CD，再得出旋转角∠BGN的度数即可得出答案．
【详解】解：过点G作MN，使∠EHD＝∠EGN=80°，
∴MN//CD，
∵∠EGB＝100°，
∴∠BGN=∠EGB-∠EGN=100°-80°=20°，
∴至少要旋转20°．
【点睛】本题考查了平行线的判定，以及图形的旋转，熟练掌握相关的知识是解题的关键．
15. 一个角的余角比它的补角的还少，则这个角的度数为___．
【答案】
【解析】
【分析】本题考查了余角的定义、补角的定义；理解“和为的两个角互为余角，和为的两个角互为补角．”是解题的关键．
【详解】解：设这个角为，则有
，
解得：；
故答案：．
16. 长方形的周长为，其中一边长为（其中），面积为，则与的关系式为________．
【答案】
【解析】
【分析】首先利长方形周长公式表示出长方形的另一边长，然后利用长方形的面积公式求解.
【详解】解：∵长方形的周长为，长方形的一边长为，
∴另一边长为，
则与的关系式为，
故答案为：.
【点睛】本题考查了列函数关系式，理解长方形的边长、周长以及面积之间的关系是关键.
三、解答题：本题共8小题，满分72分．在答题纸上写出必要的文字说明或演算步骤．
17. 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题考查了整式的混合运算，解题关键是掌握整式混合运算顺序和运算法则．
（1）先计算乘方，再计算除法，最后合并同类项；
（2）利用完全平方公式和平方差公式展开，最后再合并同类项．
【小问1详解】
解：原式=
=．
【小问2详解】
解：原式=
=．
18. 下面是两位同学进行整式运算的过程，请认真阅读并完成相应的任务．
化简：．
任务一：仔细检查小颖同学解题的过程，回答下列问题．
（1）第①处用到的乘法公式是_______________________；（用字母表示公式）
（2）第②处错误原因是_____________________．
任务二：
（3）小明逆用乘法对加法的分配，简便了运算，但其过程不完整，请你补全小明的过程．
【答案】（1）；（2）运用完全平方公式时漏掉这一项；（3）
【解析】
【分析】本题主要考查了整式的混合运算，
（1）利用平方差公式计算即可；
（2）根据完全平方公式解答，即可；
（3）提出公因式解答，即可．
【详解】解：（1）第①处用到的乘法公式是：
故答案为：
（2）第②处错误的原因是：运用完全平方公式时漏掉“”这一项；
（3）原式
．
19. 将长为，宽为的长方形白纸，按如图所示的方法粘合起来，粘合部分宽为．
（1）根据上图，将表格补充完整；
（2）设x张白纸粘合后的总长度为，求y与x之间的关系式；
（3）你认为白纸粘合起来的总长度可能为吗？为什么？
【答案】（1）180 （2）
（3）不能使黏合的纸片总长为，理由见解析
【解析】
【分析】本题考查的是函数关系式及探索图形变化的规律性知识，结合图形理清数量之间关系是解决此题关键．
（1）根据图形结合题意可得答案；
（2）根据题意和所给图形可得出答案；
（3）把代入（2）式时，看x的值是否为整数即可得到答案．
【小问1详解】
由题意可得，
5张白纸黏合后的长度为：．
故答案为：180．
【小问2详解】
根据题意和所给图形可得出：．
【小问3详解】
不能．理由如下：
令得：，
解得：．
∵为整数，
∴不能使黏合的纸片总长为．
20. 如图，已知BD⊥AC，EF⊥AC，D，F分别为垂足，G是AB上一点，且∠1＝∠2.试说明：∠AGD＝∠ABC.
【答案】见解析.
【解析】
【分析】由BD⊥AC，EF⊥AC推出BD∥EF，得到∠DBC＝∠1，再结合∠1＝∠2推出GD∥BC，可证∠AGD＝∠ABC.
【详解】∵BD⊥AC，EF⊥AC，
∴BD∥EF，∴∠DBC＝∠1.
∵∠1＝∠2，∴∠2＝∠DBC，
∴GD∥BC，∴∠AGD＝∠ABC.
【点睛】本题考查的知识点是平行线的判定与性质，解题的关键是熟练的掌握平行线的判定与性质.
21 先观察下列各式，再解答后面问题：
；
；
；
．
（1）乘积式中的一次项系数、常数项与两因式中的常数项有何关系？
（2）根据以上各式呈现的规律，用公式表示出来；
（3）试用你写的公式，直接写出下列两式的结果．
①_____________；
②_____________．
【答案】（1）两因式中常数项的和等于乘积中的一次项系数，常数项的积等于乘积中的常数项
（2）
（3）①；②
【解析】
【分析】本题考查了多项式乘多项式．
（1）根据乘积式中一次项系数、常数项与两因式中的常数项之间的规律作答；
（2）根据（1）中呈现的规律，列出公式；
（3）根据（2）中的公式代入计算．
【小问1详解】
解：乘积式中的一次项系数、常数项与两因式中的常数项的关系为：
两因式中常数项和等于乘积中的一次项系数，常数项的积等于乘积中的常数项；
【小问2详解】
解：公式为：
【小问3详解】
解：①
；
②
．
22. 某公交车每月的支出费用为7000元，票价为每人2元（不考虑任何优惠），设每月有x人乘坐该公交车，每月的收入与支出的差额为y元
（1）请直接写出y与x之间的关系式；
（2）列表表示：当x的值分别为3000，3300，3600，3900，4200，4500时，y的值；
（3）该公交车每天早上6∶00开班，晚上21∶00收班，其中除去午餐1小时外，其余时间都在正常运行，且每一个往返准点运行120分钟．若每月按30天计算，求该公交车每次往返平均需乘坐多少人，每月盈利可达到3080元？
【答案】（1）
（2）见解析 （3）每个往返平均有24人乘坐，该公交车的盈利可达到3080元
【解析】
【分析】本题考查了列函数解析式的应用，正确掌握相关性质内容是解题的关键．
（1）根据每月的收入与支出的差额为y元，以及收入为元，支出为7000元，进行列式，即可作答．
（2）分别把x的值为3000，3300，3600，3900，4200，4500代入，算出对应的的值，再运用列表方式表示出来，即可作答．
（3）算出一个月往返次数为，依题意设该公交车每次往返平均需乘坐人，代入，进行计算，即可作答．
【小问1详解】
解：∵票价为每人2元（不考虑任何优惠），每月有x人乘坐该公交车，
∴收入为元，
∵公交车每月的支出费用为7000元，且每月的收入与支出的差额为y元，
∴；
【小问2详解】
解：结合，列表如下：
【小问3详解】
解：∵该公交车每天早上6∶00开班，晚上21∶00收班，其中除去午餐1小时外，其余时间都在正常运行，且每一个往返准点运行120分钟．
∴每天往返次数为：（次），
则一个月往返次数为：（次），
设该公交车每次往返平均需乘坐人，
则，
解出，
∴每个往返平均有24人乘坐，该公交车的盈利可达到3080元．
23. 如图，直线与相交于A、D两点，分别与相交于分别与相交于B、F，如果，，试说明．
【答案】见解析
【解析】
【分析】本题考查了平行线的判定与性质，先根据角的等量代换，得出，证明，因为，再进行角的等量代换，可证明，即可作答．
【详解】解：∵，
∴
∴
∴
∵
∴
∴
∴．
24. 我们学过的乘法公式可以借助于图形来帮助解释、理解、记忆．
（1）请写出图1、图2、图3分别能解释的乘法公式；
图1 图2 图3
（2）请用两种不同的方法探究代数式的数量关系．
方法一：代数方法．
方法二：拼图的方法．（用4个全等的长和宽分别为a、b的长方形拼摆成一个正方形，画出你拼摆过程中能说明这几个式子数量关系的草图．）
（3）利用（2）中结论，当时，求的值．
【答案】（1），，
（2），方法见解析
（3）49
【解析】
【分析】本题主要考查了完全平方公式，掌握完全平方公式及变形，看懂和理解题图是解决本题的关键．
（1）观察题图，根据阴影部分的面积不变得结论；
（2）通过计算阴影部分的面积，发现三组量间关系；
（3）把已知代入（2）的结论求解即可．
【小问1详解】
解：图1、阴影部分的面积：
各个部分之和的面积等于大正方形面积
即；
图2、阴影部分的面积：；
图3、阴影部分的面积：．
故答案为：，，．
【小问2详解】
解：代数法：
∵，
则；
拼图法：如图4：
，
，
∴．
【小问3详解】
解：∵
．高度
10
20
30
40
50
…
下滑时间
3.25
3.01
2.81
2.66
2.56
…
小颖的方法：
解：原式
小明的方法：
解：原式
白纸张数
1
2
3
4
5
…
纸条长度
40
110
145
…
3000
3300
3600
3900
4200
4500
200
800
1400
2000