09，江苏省泰州市姜堰区2023-2024学年七年级下学期期中数学试题(无答案)

这是一份09，江苏省泰州市姜堰区2023-2024学年七年级下学期期中数学试题(无答案)，共7页。

（考试时间：120分钟 满分：150分）
请注意：1．本试卷分选择题和非选择题两个部分．
2．所有试题的答案均填写在答题卡上，答案写在试卷上无效．
第一部分 选择题（共18分）
一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．如图，直线被直线所截，图中与是一对内错角的是（ ）
第1题图
A．B．C．D．
2．若，下列各式运算正确的是（ ）
A．B．C．D．
3．下列各式从左到右的变形是因式分解的是（ ）
A．B．
C．D．
4．如图，在中，分别为的中点，且的面积为，则阴影部分的面积为（ ）
第4题图试卷源自 每日更新，汇集全国各地小初高最新试卷。A．B．C．D．
5．从前，一位庄园主把一块边长为的正方形土地租给租户李老汉．第二年，他对李老汉说：“我把这块地的一边增加，相邻的另一边减少，变成长方形土地继续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得李老汉的租地面积会（ ）
A．减少B．减少C．增加D．保持不变
6．一副三角板按如图所示放置，，，，过点的直线与过点的直线相互平行，设，，则下列关系正确的是（ ）
第6题图
A．B．C．D．
第二部分 非选择题（共132分）
二、填空题（本大题共有10小题，每小题3分，共30分．请把答案直接填写在答题卡相应位置上）
7．八边形的内角和度数为______．
8．华为Mate60搭载的芯片是麒麟9000S，该芯片采用的是5纳米制程工艺，5纳米就是0.000000005米，则0.000000005用科学记数法表示为______．
9．若有意义，则实数的取值范围是______．
10．已知三角形的两条边长为1和2，若第三条边长为整数，则这个三角形的周长为______．
11．如图，是五边形的5个外角，若，则的度数为______．
第11题图
12．若，则______．
13．已知，则的值为______．
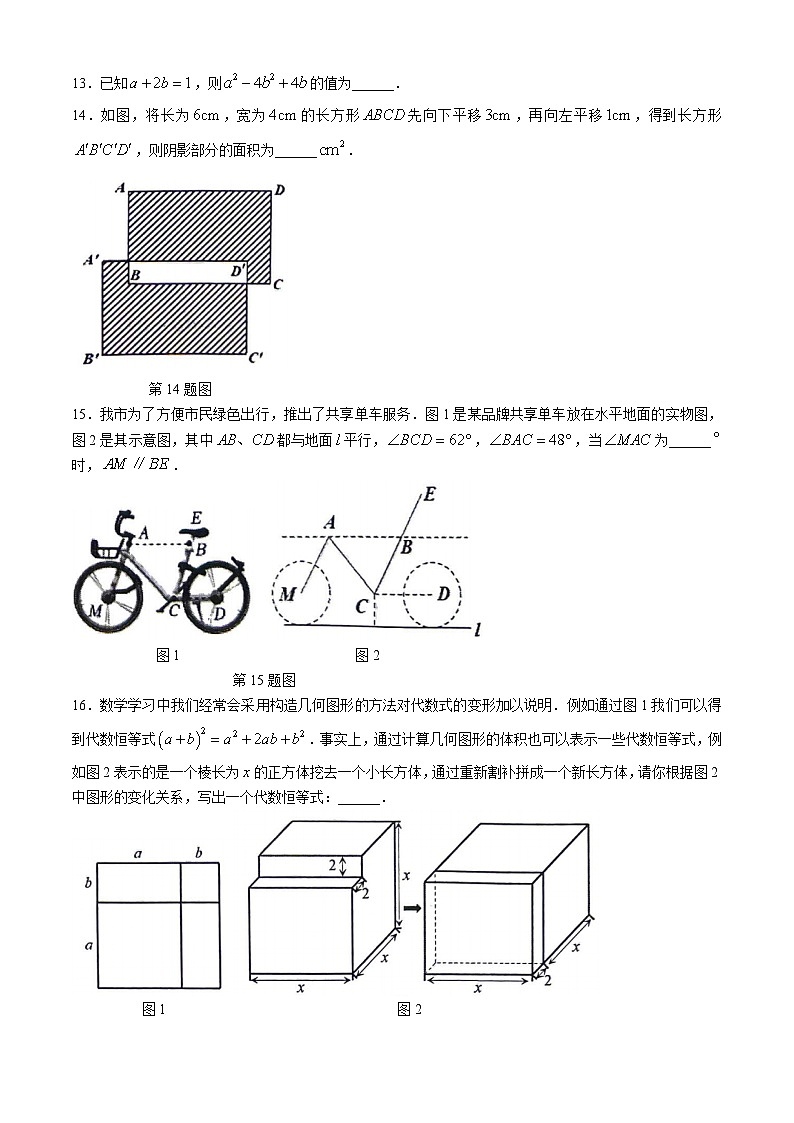
14．如图，将长为，宽为的长方形先向下平移，再向左平移，得到长方形，则阴影部分的面积为______．
第14题图
15．我市为了方便市民绿色出行，推出了共享单车服务．图1是某品牌共享单车放在水平地面的实物图，图2是其示意图，其中都与地面平行，，，当为______时，．

图1 图2
第15题图
16．数学学习中我们经常会采用构造几何图形的方法对代数式的变形加以说明．例如通过图1我们可以得到代数恒等式．事实上，通过计算几何图形的体积也可以表示一些代数恒等式，例如图2表示的是一个棱长为的正方体挖去一个小长方体，通过重新割补拼成一个新长方体，请你根据图2中图形的变化关系，写出一个代数恒等式：______．
图1 图2
第16题图
三、解答题（本大题共10小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（本题满分16分）
计算：（1）；（2）；
（3）；（4）．
18．（本题满分8分）
因式分解：（1）；（2）．
19．（本题满分8分）
先化简，再求值：，其中，．
20．（本题满分8分）
已知，．
（1）求的值；
（2）求的值；
（3）当时，求的值．
21．（本题满分8分）
王老师在数学课上带领同学们做等式接龙游戏，他在黑板上写下4个等式：
①；②；③；④．
他要求同学们根据黑板上已写等式的规律，再任意写出一个等式．
下面是3位同学的接龙等式：
⑤；⑨； eq \\ac(○,15)
（1）上面3位同学的接龙等式与其他等式规律不相同的是______；（填序号）
（2）探索以上等式的规律，写出第个等式，并说明第个等式成立的理由．
22．（本题满分8分）
小明同学在做家庭作业时，其中一道题被调皮的弟弟涂花了，如下所示：
如图，在中，，，试说明：．
第22题图
解：（已知），
（），
（两直线平行，内错角相等），
（已知），
（等量代换），
（）．
（1）请你从下列选项中选出合适的理由或结论帮小明将涂花的过程补全，将所选序号按说理顺序填写在横线上：______，______，______；
①同旁内角互补，两直线平行；②两直线平行，同位角相等；③同位角相等，两直线平行；④；⑤．
（2）若，，求的度数．
23．（本题满分10分）
阅读材料：已知，，求的值．
解：，
，
，
，
．
根据上面的解题思路与方法，解决下列问题：
（1）若，，则______；
（2）若，求的值；
（3）若，，求的值．
24．（本题满分10分）
如图，在四边形中，，的角平分线交于点．
第24题图
（1）若，求的度数；
（2）用无刻度的直尺和圆规过点作，交于点；（不写作法，保留作图痕迹）
（3）在（2）的条件下，请判断是否平分，并说明理由．
25．（本题满分12分）
小丽在进行因式分解时发现一个现象，关于的二次多项式若能分解成两个一次整式相乘的形式，当或时，原多项式的值为0，则定义和为多项式的“零值”，两个“零值”的平均值为多项式的“对称值”．例如：，当或时，的值为0，则多项式的“零值”为和，的“对称值”为．
根据上述材料，解决下列问题：
（1）多项式的“零值”为______，“对称值”为______；
（2）若关于的多项式的两个“零值”相等，求的值以及多项式的“对称值”；
（3）若关于的多项式有一个“零值”为，关于的另一个多项式与多项式的“对称值”相同，且多项式的两个“零值”之比是，求的值．
26．（本题满分14分）
数学活动课上，老师给兴趣小组的同学们布置了一道探究题：在中，，平分，于点，，交直线于点．猜想与和的数量关系．
同学们通过画图计算等方法进行推理，得到了有关成果．下面是三个兴趣小组成员进行交流展示时的部分成果，请同学们借助展示成果来完成任务．
任务一：
如图1，根据“智慧小组”的计算表格，可知______，猜想与的数量关系为______；
任务二：
若，请你根据图2，判断“任务一”中与的数量关系是否依然成立？若成立，请说明理由；若不成立，请写出它们所满足的数量关系，并说明理由；
任务三：
在中，若将条件“”改为“”，其他条件不变，请画出符合条件的所有不同类型的图形，并直接写出与对应的数量关系．素材1
度
60
70
60
80
80
度
10
20
30
20
40
度
25
a
15
30
20
素材2
图2
思考分享
“智慧小组”
“创新小组”
“奋斗小组”
如图1，，设置表格，尝试代入的值，求的值，得到几组对应值．
若，根据题目条件，作出图2．
通过推理发现，当时，点重合，故
反思
……