2025届高考数学一轮总复习第一章集合与常用逻辑用语第二节常用逻辑用语课件

这是一份2025届高考数学一轮总复习第一章集合与常用逻辑用语第二节常用逻辑用语课件，共38页。PPT课件主要包含了内容索引，强基础增分策略，增素能精准突破，充分不必要，必要不充分，既不充分也不必要，全称量词，存在量词，答案A，答案D等内容，欢迎下载使用。

知识梳理1.充分条件、必要条件、充要条件(1)充分条件、必要条件、充要条件的概念若p⇒q,则p是q的　　　　条件,q是p的　　　　条件;若p⇒q且q⇒p,则p是q的充分必要条件,简称充要条件. 
(2)充分条件、必要条件、充要条件的划分
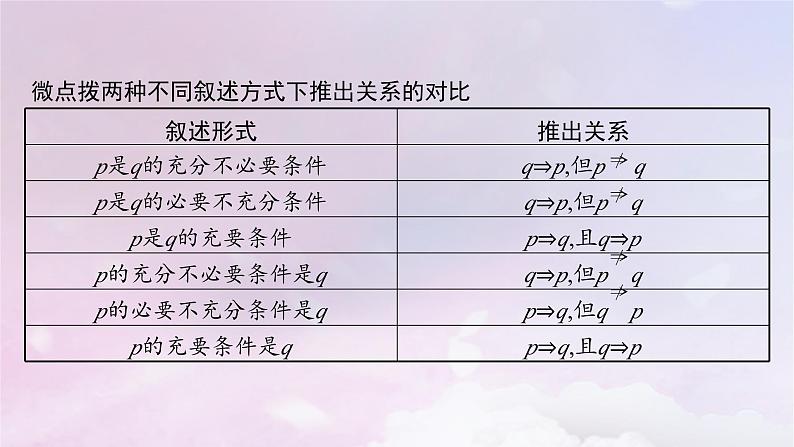
微点拨两种不同叙述方式下推出关系的对比
2.全称量词命题与存在量词命题(1)全称量词与存在量词①短语“所有的”“任意一个”在逻辑中通常叫做　　　　　　,并用符号“∀”表示. ②短语“存在一个”“至少有一个”在逻辑中通常叫做　　　　　　,并用符号“∃”表示. 
(2)全称量词命题与存在量词命题及其否定.
　　有些命题中省略了量词,在进行否定时应改写为完整形式,再进行否定
∃x∈M,¬p(x)
∀x∈M,¬p(x)
微点拨全称量词命题与存在量词命题的真假判断(1)全称量词命题的真假判断:要判断一个全称量词命题是真命题,必须对限定集合M中的每一个元素x,验证p(x)成立;但要判断一个全称量词命题是假命题,只需列举出一个x∈M,使得p(x)不成立即可.(2)存在量词命题的真假判断:要判断一个存在量词命题是真命题,只要在限定集合M中,能找到一个x,使得p(x)成立即可;否则这一命题就是假命题.
常用结论1.若p,q中所涉及的问题与变量有关,记p,q中相应变量的取值集合分别记为A,B,那么有以下结论:
2.p是q的充分不必要条件⇔¬p是¬q的必要不充分条件.3.以下说法是等价的:①p⇒q;②p是q的充分条件;③q是p的必要条件;④q的充分条件是p;⑤p的必要条件是q.4.全称量词命题(或存在量词命题)与其否定的真假性恰好相反.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)当q是p的必要条件时,p是q的充分条件.(　　)(2)“α≠β”是“sin α≠sin β”的充要条件.(　　)(3)写存在量词命题的否定时,存在量词应变为全称量词.(　　)(4)若p是q的充分不必要条件,q是r的充分不必要条件,则r是p的必要不充分条件.(　　)
2.下列命题既是真命题又是存在量词命题的是(　　)A.存在θ,使tan θ=tan(90°-θ)B.存在实数x,使sin x=C.对一切θ,使sin θ=sin(180°-θ)D.sin(α-β)=sin αcs β-cs αsin β
解析 只有A,B两个选项中的命题是存在量词命题,因为|sin x|≤1,所以sin x= 不成立,故B中命题为假命题.因为当θ=45°时,tan θ=tan(90°-θ),故A中命题为真命题.
3.“x>y>0”是下列哪一项的必要不充分条件(　　)
考向1.充分条件与必要条件的判断典例突破
例1.(1)(2023天津,2)“a2=b2”是“a2+b2=2ab”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(2)设x∈R,则“sin x=1”是“cs x=0”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
(3)若α,β表示两个不同的平面,m为平面α内的一条直线,则(　　)A.“m∥β”是“α∥β”的充分不必要条件B.“m∥β”是“α∥β”的必要不充分条件C.“m⊥β”是“α⊥β”的必要不充分条件D.“m⊥β”是“α⊥β”的充要条件
答案 (1)B　(2)A　(3)B　
解析(1)由a2+b2=2ab,得(a-b)2=0,所以a=b.所以a2=b2,故必要性成立;又当a=1,b=-1时,满足a2=b2,而a2+b2=2ab不成立,故充分性不成立.所以“a2=b2”是“a2+b2=2ab”的必要不充分条件.故选B.
(3)当m∥β时,不一定有α∥β,也可能α,β相交,但当α∥β时,必有m∥β,即“m∥β”是“α∥β”的必要不充分条件,故A错误,B正确;当m⊥β时,α⊥β,当α⊥β时,不一定有m⊥β,故“m⊥β”是“α⊥β”的充分不必要条件,故C,D均错误.
对点训练1(1)已知非零向量a,b,给定p:∃λ∈R,使得a=λb,q:|a+b|=|a|+|b|,则p是q的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
答案 (1)B　(2)A　
考向2.充分条件与必要条件的探求典例突破例2.已知向量a=(x,y),b=(cs α,sin α),其中x,y,α∈R.若|a|=4|b|,则“a·b<λ2”的一个必要不充分条件是(　　)A.λ>3或λ<-3B.λ>1或λ<-1C.-3<λ<3D.-1<λ<1
技巧点拨探求充分条件与必要条件的方法(1)探求一个说法成立的充分不必要条件和必要不充分条件时,可以先找到其成立的充要条件,然后通过对充要条件的范围缩小或放大,得到相应的充分不必要条件和必要不充分条件.(2)如果p是q的充分不必要条件,那么p并不是唯一的,可以有多个;同样,如果p是q的必要不充分条件,那么p也不是唯一的,可以有多个.
对点训练2下面四个条件中,是“a>b”的充分不必要条件的是(　　)
考向3.由充分条件或必要条件求参数取值范围典例突破例3.若“a≤k”是“一次函数y=(a-3)x+(a-2)的图象不经过第一象限”的充分不必要条件,则实数k的取值范围是　　　　　. 
答案 (-∞,2)　
解析 若一次函数y=(a-3)x+(a-2)的图象不经过第一象限,则 解得a≤2,即“一次函数y=(a-3)x+(a-2)的图象不经过第一象限”的充要条件是“a≤2”,因此,若“a≤k”是“一次函数y=(a-3)x+(a-2)的图象不经过第一象限”的充分不必要条件,则k<2.
名师点析根据充分条件与必要条件求参数取值范围的步骤(1)记集合M={x|p(x)},N={x|q(x)};(2)根据以下表格确定集合M与N的包含关系:
(3)根据集合M与N的包含关系建立关于参数的不等式(组);(4)解不等式(组)求出参数的取值范围.
对点训练3(已知p:x≥a,q:|x+2a|<3,且p是q的必要不充分条件,则实数a的取值范围是(　　)A.(-∞,-1]B.(-∞,-1)C.[1,+∞)D.(1,+∞)
考向1.含有一个量词的命题的否定典例突破
解析 根据全称量词命题的否定是存在量词命题可得,该命题的否定为∃x>1, ≤0,故选D.
名师点析含有一个量词的命题的否定对一个全称量词命题或存在量词命题进行否定时,必须要把命题的两个地方进行改变,一是量词要改变,二是结论要进行否定,即“改变量词,否定结论”.
对点训练4已知命题p:所有的三角函数都是周期函数,则¬p为(　　)A.所有的周期函数都不是三角函数B.所有的三角函数都不是周期函数C.有些周期函数不是三角函数D.有些三角函数不是周期函数
考向2.全称量词命题与存在量词命题的真假判断典例突破
例5.(多选)(2023云南安宁一中模拟)下列命题的否定中,是真命题的有(　　)A.某些平行四边形是菱形B.∃x∈R,x2-3x+3<0C.∀x∈R,|x|+x2≥0D.∀a∈R,关于x的方程x2-ax+1=0有实数解
解析 对于A,某些平行四边形是菱形,是真命题;对于B,因为Δ=9-12=-3<0,所以x2-3x+3>0恒成立,故原命题是假命题;对于C,∀x∈R,|x|+x2≥0,是真命题;对于D,只有Δ=a2-4≥0,即a≤-2或a≥2时,x2-ax+1=0有实数解,是假命题.根据原命题和它的否定真假性相反判断,选项B,D中原命题的否定是真命题.故选BD.
对点训练5下列命题为假命题的是(　　)A.∃a∈R,y=2x-a·2-x为偶函数
D.∀x∈R,x4考向3.根据命题的真假求参数的取值范围典例突破
答案 (-∞,-1)　
例6.(2023江西南昌模拟)已知命题p:∀x∈R,a<3x2 024+1,若p为真命题,则实数a的取值范围是　　　　　　. 
解析若∀x∈R,a<3x2 024+1为真命题,则a<(3x2 024+1)min,∵x2 024≥0,当且仅当x=0时,等号成立,∴3x2 024+1≥1,即(3x2 024+1)min =1,故实数a的取值范围是(-∞,1).
名师点析应用全称量词命题与存在量词命题求参数取值范围的注意点(1)全称量词命题多与“恒成立”问题有关,全称量词命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以可以代入求解,也可以根据函数或不等式中恒成立问题的求解方法求解.(2)存在量词命题多以适合某种条件的结论“存在”“不存在”等语句表达.解答这类问题,一般要先对结论做出肯定存在的假设,再从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致了矛盾,则否定了假设.