





华师大版七年级下册9.2 多边形的内角和与外角和课文课件ppt
展开
这是一份华师大版七年级下册9.2 多边形的内角和与外角和课文课件ppt,共14页。PPT课件主要包含了学习目标,重难点,知识回顾,教学过程,探究新知,例题精讲等内容,欢迎下载使用。
1.理解多边形及其相关概念.2.掌握多边形的内角和与外角和公式.3.能够灵活运用多边形的内角和定理和外角和定理解决问题.
重点:多边形的内角和公式与外角和.难点:多边形的内角和,外角和定理的推导.
什么叫三角形? 三角形的内角和是多少?什么叫三角形的外角?什么叫外角和?三角形的外角和是多少?
解:三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形.三角形的内角和是180°.三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角.从与三角形每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.三角形的外角和等于360°.
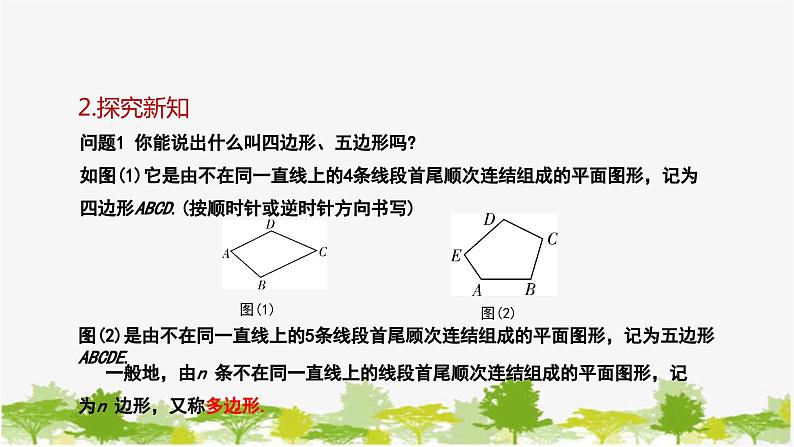
问题1 你能说出什么叫四边形、五边形吗?如图(1)它是由不在同一直线上的4条线段首尾顺次连结组成的平面图形,记为四边形ABCD.(按顺时针或逆时针方向书写)
一般地,由n 条不在同一直线上的线段首尾顺次连结组成的平面图形,记为n 边形,又称多边形.
图(2)是由不在同一直线上的5条线段首尾顾次连结组成的平面图形,记为五边形ABCDE.
与三角形类似,如图,∠A、∠D、∠C、∠ABC 是四边形ABCD 的四个内角,∠CBE 和∠ABF,这两个外角是对顶角.(一个n 边形有n 个内角,有2n 个外角) 如果多边形的各边都相等,各内角也都相等,则称为正多边形,如正三角形、正四边形(正方形)、正五边形等等. 连结多边形不相邻的两个顶点的线段叫做多边形的对角线,如图(1),线段AC 是四边形 ABCD 的对角线,如图(2),线段AD、AC 是五边形ABCDE 的对角线,如图3中线段AC、AD、AE 是六边形ABCDEF 的对角线.
问:(1)四边形有几条对角线? (2)五边形有几条对角线? (3)六边形有几条对角线? 那n 边形呢?
问题2 三角形的内角和等于180°,那么一般n 边形是否也有内角和公式呢?
由此得出:n 边形的内角和=(n-2)·180°
问题3 与多边形的每个内角相邻的外角有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.多边形的外角和应该等于多少呢?下面我们也来探讨.
任意多边形的外角和都为360°.
【知识归纳】(1)由n 条不在同一直线上的线段首尾顺次连结组成的平面图形,记为n 边形,又称多边形.(2)如果多边形的各边都相等,各内角也都相等,则称为正多边形.(3)连结多边形不相邻的两个顶点的线段叫做多边形的对角线.(4)n 边形的内角和=(n-2)·180°.(5)任意多边形的外角和都为360°.
例1 求八边形的内角和.
解:八边形的内角和为(8-2)×180°= 1080°.
例2 一个多边形的内角和等于2160°,求这个多边形的边数?
解:设这个多边形的边数为n,根据题意, 得(n -2 )×180°= 2160°,解得n = 14. 即这个多边形的边数为14.
例3 一个多边形的每个外角都是72°,这个多边形是几边形?.
解:设多边形的边数为n,根据题意,得n·72°=360°.解得n =5. 因此这个多边形是五边形.
例4 已知一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
解:设多边形的边数为n.∵它的内角和等于 (n-2)•180°,多边形外角和等于360°,∴ (n-2)•180°=5× 360°.解得n =12.∴这个多边形的边数为12.这个多边形是十二边形.
4.巩固练习 完成教材课后同步练习
相关课件
这是一份华师大版七年级下册9.2 多边形的内角和与外角和说课ppt课件,共32页。PPT课件主要包含了n–2,从图中可以知道,n·180°等内容,欢迎下载使用。
这是一份初中数学华师大版七年级下册第9章 多边形9.2 多边形的内角和与外角和课文内容课件ppt,共24页。
这是一份初中数学华师大版七年级下册9.2 多边形的内角和与外角和课堂教学ppt课件,文件包含第1课时多边形及其内角和pptx、第2课时多边形的外角和pptx等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。









