专题14 二次函数与几何压轴（3题型+16类型）（讲练）-2024年中考数学二轮复习讲义（全国通用）

这是一份专题14 二次函数与几何压轴（3题型+16类型）（讲练）-2024年中考数学二轮复习讲义（全国通用），文件包含专题14二次函数与几何压轴讲练原卷版docx、专题14二次函数与几何压轴讲练解析版docx等2份试卷配套教学资源，其中试卷共188页， 欢迎下载使用。

一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
专题14 二次函数与几何压轴
目 录
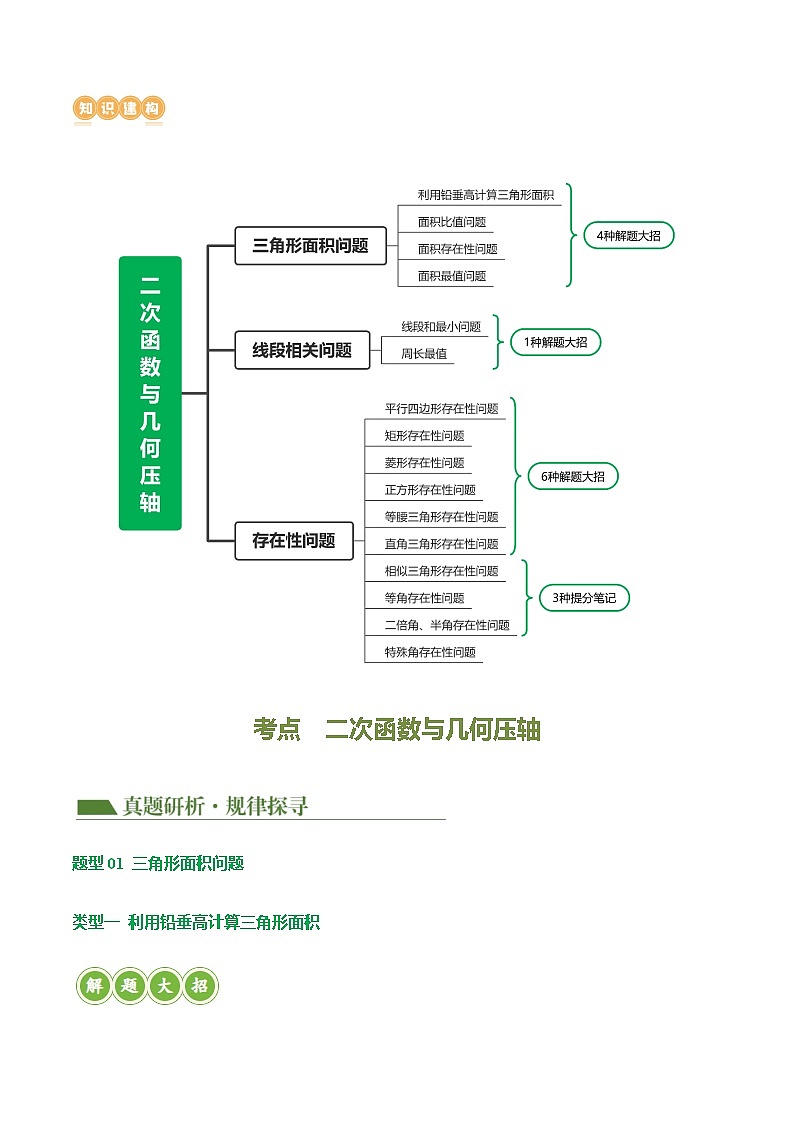
TOC \ "1-3" \n \h \z \u \l "_Tc160094594" 一、考情分析
二、知识建构
\l "_Tc162384457" 考点 二次函数与几何压轴
\l "_Tc162384458" \l "_Tc161932549" \l "_Tc161309508" \l "_Tc160094596" \l "_Tc160094596" 【真题研析·规律探寻】
\l "_Tc162384459" 题型01 三角形面积问题
\l "_Tc162384460" 类型一 利用铅垂高计算三角形面积
\l "_Tc162384461" 类型二 面积比值问题
\l "_Tc162384462" 类型三 面积存在性问题
\l "_Tc162384463" 类型四 面积最值问题
\l "_Tc162384464" 题型02 线段相关问题
\l "_Tc162384465" \l "_Tc162384466" 类型一 线段和最小问题
\l "_Tc162384467" 类型二 周长最值
\l "_Tc162384468" 题型03 存在性问题
\l "_Tc162384469" 类型一 平行四边形存在性问题
\l "_Tc162384470" 类型二 矩形存在性问题
\l "_Tc162384471" 类型三 菱形存在性问题
\l "_Tc162384472" 类型四 正方形存在性问题
\l "_Tc162384473" 类型五 等腰三角形存在性问题
\l "_Tc162384474" 类型六 直角三角形存在性问题
\l "_Tc162384475" 类型七 相似三角形存在性问题
\l "_Tc162384476" 类型八 等角存在性问题
\l "_Tc162384477" 类型九 二倍角、半角存在性问题
\l "_Tc162384478" 类型十 特殊角存在性问题
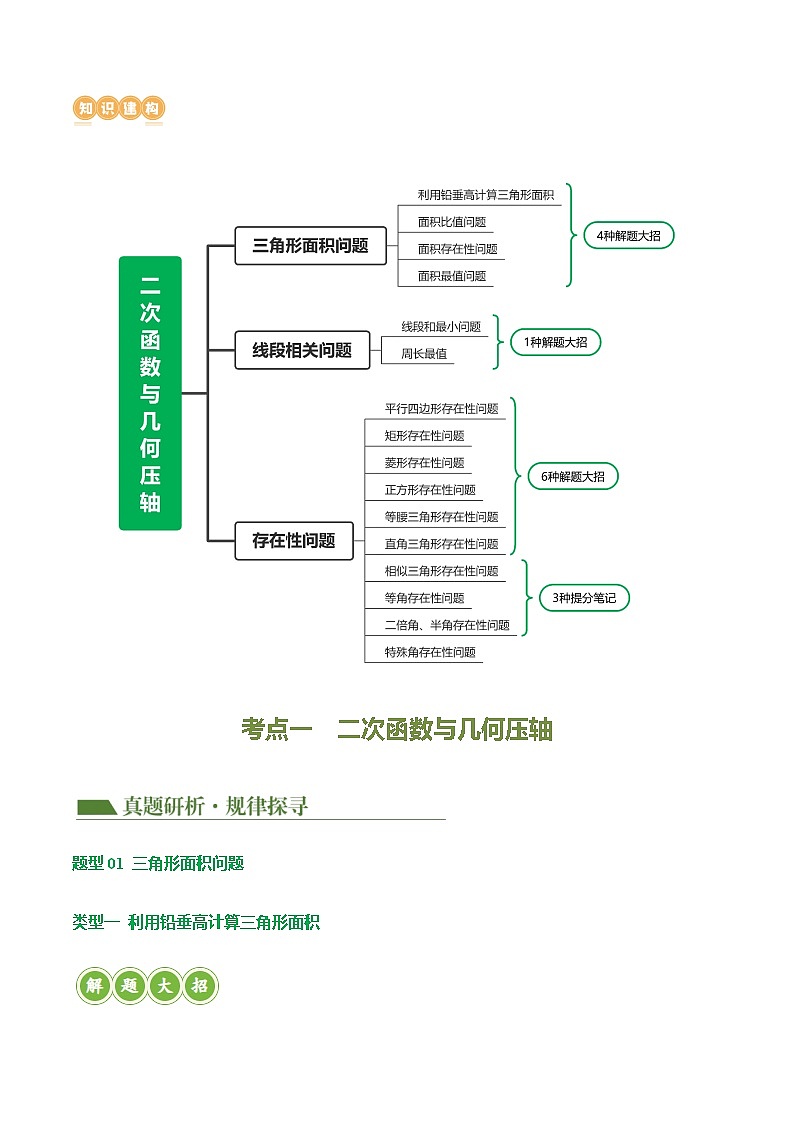
\l "_Tc162384479" \l "_Tc161932561" \l "_Tc161309520" \l "_Tc160094605" 【好题必刷·强化落实】
考点一 二次函数与几何压轴
题型01 三角形面积问题
类型一 利用铅垂高计算三角形面积
1．（2023·黑龙江牡丹江·中考真题）如图，抛物线y=x2+bx+c与x轴交于点A−1,0，B4,0，与y轴交于点C．

(1)求抛物线对应的函数解析式，并直接写出顶点P的坐标；
(2)求△BCP的面积．
注：抛物线y=ax2+bx+ca≠0的对称轴是直线x=−b2a，顶点坐标是−b2a,4ac−b24a．
【答案】(1)抛物线对应的解析式y=x2−3x−4，P32,−254
(2)S△BCP=152
【分析】（1）利用待定系数法求出抛物线的表达式，再根据解析式求点P的坐标即可；
（2）求出点C0,−4和抛物线顶点P32,−254，A−1,0，B4,0利用S△BCP=S△OCP+S△OBP−S△BOC即可得到答案．
【详解】（1）∵抛物线y=x2+bx+c经过点A−1,0，B4,0，
∴1−b+c=016+4b+c=0，
解这个方程组，得b=−3c=−4．
∴抛物线对应的解析式y=x2−3x−4．
∵P点是抛物线的顶点坐标，
∴P−b2a,4ac−b24a，即：−b2a=−−32×1=32，4ac−b24a=4×1×−4−−324×1=−254，
∴P32,−254．
（2）如图，连接OP．

∵A−1,0，B4,0，C0,−4，P32,−254，
∴S△OCP=12×4×32=3，
S△OBP=12×4×254=252，
S△BOC=12×4×4=8．
∵S△BCP=S△OCP+S△OBP−S△BOC，
∴S△BCP=3+252−8=152．
【点睛】此题考查待定系数法求二次函数解析式、二次函数的图象和性质等知识，掌握数形结合的思想和割补法求三角形面积是解题的关键．
2．（2023·湖南常德·中考真题）如图，二次函数的图象与x轴交于A−1,0，B5,0两点，与y轴交于点C，顶点为D．O为坐标原点，tan∠ACO=15．

(1)求二次函数的表达式；
(2)求四边形ACDB的面积；
(3)P是抛物线上的一点，且在第一象限内，若∠ACO=∠PBC，求P点的坐标．
【答案】(1)y=−x+1x−5
(2)30
(3)P12,274
【分析】（1）用两点式设出二次函数的解析式，然后求得C点的坐标，并将其代入二次函数的解析式，求得a的值，再将a代入解析式中即可．
（2）先将二次函数变形为顶点式，求得顶点坐标，然后利用矩形、三角形的面积公式即可求得答案．
（3）根据各点的坐标的关系及同角三角函数相等的结论可以求得相关联的函数解析式，最后联立一次函数与二次函数的解析式，求得点P的坐标．
【详解】（1）∵二次函数的图象与x轴交于A−1,0,B5,0两点．
∴设二次函数的表达式为y=ax+1x−5
∵AO=1,tan∠ACO=15，
∴OC=5，即C的坐标为0,5
则5=a0+10−5，得a=−1
∴二次函数的表达式为y=−x+1x−5；
（2）y=−x+1x−5=−(x−2)2+9
∴顶点的坐标为2,9
过D作DN⊥AB于N，作DM⊥OC于M，
四边形ACDB的面积=S△AOC+S矩形OMDN−S△CDM+S△DNB
=12×1×5+2×9−12×2×9−5+12×5−2×9=30；

（3）如图，P是抛物线上的一点，且在第一象限，当∠ACO=∠PBC时，
连接PB，过C作CE⊥BC交BP于E，过E作EF⊥OC于F，

∵OC=OB=5，则△OCB为等腰直角三角形，∠OCB=45°．
由勾股定理得：CB=52，
∵∠ACO=∠PBC，
∴tan∠ACO=tan∠PBC，
即15=CECB=CE52，
∴CE=2
由CH⊥BC，得∠BCE=90°，
∴∠ECF=180°−∠BCE−∠OCB=180°−90°−45°=45°．
∴△EFC是等腰直角三角形
∴FC=FE=1
∴E的坐标为1,6
所以过B、E的直线的解析式为y=−32x+152
令y=−32x+152y=−x+1x−5
解得x=5y=0，或x=12y=274
所以BE直线与抛物线的两个交点为B5,0,P12,274
即所求P的坐标为P12,274
【点睛】本题考查了一次函数、二次函数的性质以及与坐标系几何图形的综合证明计算问题，解题的关键是将所学的知识灵活运用．
类型二 面积比值问题
情况一：等底或等高
S△ABCS△BCD=AEDF S△ABCS△ACD=BCCD
结论：①当底相等，则面积比=高之比 ②当高相等，则面积比=底边之比
情况二：斜转直
1．（2020·四川成都·中考真题）在平面直角坐标系xOy中，已知抛物线y=ax2+bx+c与x轴交于A(−1,0)，B(4,0)两点，与y轴交于点C(0,−2)．
（1）求抛物线的函数表达式
（2）如图1，点D为第四象限抛物线上一点，连接AD，BC交于点E，连接BD，记ΔBDE的面积为S1，ΔABE的面积为S2，求S1S2的最大值；
（3）如图2，连接AC，BC，过点O作直线l//BC，点P，Q分别为直线和抛物线上的点．试探究：在第一象限是否存在这样的点P，Q，使ΔPQB∽ΔCAB．若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
【答案】（1）y=12x2−32x−2；（2）45；（3）存在，689,349或6+2415,3+415
【分析】（1）利用待定系数法进行求解即可；
（2）过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴交BC的延长线于点K，则可得△AEK∽△DEF，继而可得DEAE=DFAK，先求出BC的解析式，继而求得AK长，由S1S2=SΔBDESΔABE=DEAE可得S1S2=DFAK，设点Dm,12m2−32m−2，进而可得DF=−12m2+2m，从而可得S1S2=−15m2+45m，再利用二次函数的性质即可求得答案；
（3）先确定出∠ACB=90°，再得出直线l的表达式为y=12x．设点P的坐标为t,t2，然后分点P在直线BQ右侧，点P在直线BQ左侧两种情况分别进行讨论即可．
【详解】（1）∵抛物线y=ax2+bx+c与x轴交于A(−1,0)，B(4,0)两点，与y轴交于点C(0,−2)．
∴a−b+c=016a+4b+c=0c=−2，
∴a=12c=−2b=−32，
∴抛物线的函数表达式为y=12x2−32x−2；
（2）过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴交BC的延长线于点K．
则DG//AK，
∴△AEK∽△DEF，
∴DEAE=DFAK，
设直线BC的解析式为y=kx+n，
将B(4,0)、C(0,−2)代入则有：4k+n=0n=−2，
解得k=12n=−2，
∴直线BC的表达式为y=12x−2，
当x=-1时，y=12x−2=−52，
即K（-1，−52），
∴AK=52．
∵S1S2=SΔBDESΔABE=DEAE．
∴S1S2=DFAK
设点Dm,12m2−32m−2，则F点坐标为（m，12m−2），
∴DF=12m−2−12m2−32m−2=−12m2+2m．
∴S1S2=−12m2+2m52=−15m2+45m=−15m−22+45，
当m=2时，S1S2有最大值45．
（3）∵A(−1,0)，B(4,0)，C(0,−2)．
∴AC=12+22=5，BC=42+22=25，AB=5，
∴AC2+BC2=25=52=AB2，
∴∠ACB=90°，
∵过点O作直线l//BC，直线BC的表达式为y=12x−2，
∴直线l的表达式为y=12x．
设点P的坐标为t,t2．
①当点P在直线BQ右侧时，如图，∠BPQ=90°，过点P作PN⊥x轴于点N，过点Q作QM⊥PN于点M，
∴∠M=∠PNB=90°，
∴∠BPN+∠PBN=90°，
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°，
∴∠QPM=∠PBN，
∴ΔQPM∽ΔPBN，
∴QMPN=PMBN=PQPB，
又∵ΔPQB∽ΔCAB，
∴PQPB=CABC，
∴QMPN=PMBN=PQPB=CABC=12，
∵NB=t-4，PN=t2，
∴QMt2=PMt−4=12，
∴QM=t4，PM=12t−2，
∴MN=12t−2+12t=t−2，t−t4=34t，
∴点Q的坐标为34t,t−2．
将点Q的坐标为34t,t−2代入y=12x2−32x−2，得
t−2=932t2−98t−2，
解得：t1=689，t2=0（舍去），
此时点P的坐标为689,349．
②当点P在直线BQ左侧时．如图，∠BPQ=90°，过点P作PN⊥x轴于点N，过点Q作QM⊥PN于点M，
∴∠M=∠PNB=90°，
∴∠BPN+∠PBN=90°，
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°，
∴∠QPM=∠PBN，
∴ΔQPM∽ΔPBN，
∴QMPN=PMBN=PQPB，
又∵ΔPQB∽ΔCAB，
∴PQPB=CABC，
∴QMPN=PMBN=PQPB=CABC=12，
∵NB=4-t，PN=t2，
∴QMt2=PM4−t=12，
∴QM=t4，PM=2−12t，
∴MN=2−12t+12t=2，t+t4=54t，
∴点Q的坐标为54t,2．
将点Q的坐标为54t,2代入y=12x2−32x−2，得
2=2532t2−158t−2，
解得：t1=6+2415，t2=6−2415<0（舍去），
此时点P的坐标为6+2415,3+415．
【点睛】本题是二次函数综合题，涉及了待定系数法，二次函数的性质，勾股定理的逆定理，相似三角形的判定与性质等，综合性较强，难度较大，熟练掌握相关知识，正确进行分类讨论是解题的关键．
2．（2022·福建·中考真题）在平面直角坐标系xOy中，已知抛物线y=ax2+bx经过A（4，0），B（1，4）两点．P是抛物线上一点，且在直线AB的上方．
(1)求抛物线的解析式；
(2)若△OAB面积是△PAB面积的2倍，求点P的坐标；
(3)如图，OP交AB于点C，PD∥BO交AB于点D．记△CDP，△CPB，△CBO的面积分别为S1，S2，S3．判断S1S2+S2S3是否存在最大值．若存在，求出最大值；若不存在，请说明理由．
【答案】(1)y=−43x2+163x
(2)存在，2,163或（3，4）
(3)存在，98
【分析】（1）待定系数法求解析式即可求解；
（2）待定系数法求得直线AB的解析式为y=−43x+163，过点P作PM⊥x轴，垂足为M，PM交AB于点N．过点B作BE⊥PM，垂足为E．可得S△PAB=S△PNB+S△PNA =32PN，设Pm,−43m2+163m1（3）由已知条件可得△OBC∽△PDC，进而可得S1S2+S2S3=CDBC+PCOC =2PDOB，过点B,P分别作x轴的垂线，垂足分别F,E，PE交AB于点Q，过D作x的平行线，交PE于点G，可得△DPG∽△OBF，设Pm,−43m2+163m1【详解】（1）解：（1）将A（4，0），B（1，4）代入y=ax2+bx，
得16a+4b=0a+b=4，
解得a=−43b=163．
所以抛物线的解析式为y=−43x2+163x．
（2）设直线AB的解析式为y=kx+tk≠0，
将A（4，0），B（1，4）代入y=kx+t，
得4k+t=0k+t=4，
解得k=−43t=163．
所以直线AB的解析式为y=−43x+163．
过点P作PM⊥x轴，垂足为M，PM交AB于点N．
过点B作BE⊥PM，垂足为E．
所以S△PAB=S△PNB+S△PNA
=12PN×BE+12PN×AM
=12PN×BE+AM
=32PN．
因为A（4，0），B（1，4），所以S△OAB=12×4×4=8．
因为△OAB的面积是△PAB面积的2倍，
所以2×32PN=8，PN=83．
设Pm,−43m2+163m1所以PN=−43m2+163m−−43m+163=83，
即−43m2+203m−163=83，
解得m1=2，m2=3．
所以点P的坐标为2,163或（3，4）．
（3）∵ PD∥BO
∴△OBC∽△PDC
∴CDBC=PDOB=PCOC
记△CDP，△CPB，△CBO的面积分别为S1，S2，S3．则S1S2+S2S3=CDBC+PCOC =2PDOB
如图，过点B,P分别作x轴的垂线，垂足分别F,E，PE交AB于点Q，过D作x的平行线，交PE于点G
∵B1,4，
∴F1,0
∴OF=1
∵PD∥OB,DG∥OF
∴△DPG∽△OBF
∴PDOB=PGBF=DGOF，
设Pm,−43m2+163m1∵直线AB的解析式为y=−43x+163．
设Dn,−43n+163，则Gm,−43n+163
PG=−43m2+163m+43n−163
=43m2−4m−n+4
DG=m−n
∴43(m2−4m−n+4)4=m−n1
整理得4n=m2−m+4
∴ S1S2+S2S3=CDBC+PCOC =2PDOB
=2DGOF
=2m−n
=2m−m2−m+44
=−12m2−5m+4
=−12m−522+98
∴m=52时，S1S2+S2S3取得最大值，最大值为98
【点睛】本题考查了二次函数综合，待定系数法求解析式，面积问题，相似三角形的性质与判定，第三问中转化为线段的比是解题的关键．
类型三 面积存在性问题
等积变形原理：S△ABC=S△BCD=S△BCE
情况一：公共边为定边
题目要求：在抛物线上找一点P，使得S△ABC=S△PBC
方法简介：
①A.P在公共边BC同侧时，只需AP∥BC，过点A作l1//BC，交抛物线于P1.
②A.P在公共边BC异侧时，将l1上移2CD个单位，即CD=CE，记为l2//BC, 交抛物线于P2，P3
③将l1和l2分别与抛物线联立.
情况二：公共边为动边
题目要求：在抛物线上找一点P，使得S△APB=S△APC
方法简介：
①当点B.C在公共边AP同侧时，只需AP //BC即可，过点A作l//BC交抛物线于P1，联立l与抛物线.
②当点B.C在公共边AP异侧时，取BC中点D，CM=BN连接AD交抛物线于P2，联立AD与抛物线.

1．（2023·湖南·中考真题）如图，二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于C点，其中B1,0，C0,3．

(1)求这个二次函数的表达式；
(2)在二次函数图象上是否存在点P，使得S△PAC=S△ABC？若存在，请求出P点坐标；若不存在，请说明理由；
(3)点Q是对称轴l上一点，且点Q的纵坐标为a，当△QAC是锐角三角形时，求a的取值范围．
【答案】(1)y=x2−4x+3
(2)P2,−1或P3−172,7+172或P3+172,7−172
(3)3+172【分析】（1）待定系数法求解析式即可求解；
（2）根据S△PAC=S△ABC，可得P到AC的距离等于B到AC的距离，进而作出两条AC的平行线，求得解析式，联立抛物线即可求解；
（3）根据题意，求得当△QAC是直角三角形时的a的值，进而观察图象，即可求解，分a>0和a<0两种情况讨论，分别计算即可求解．
【详解】（1）解：将点B1,0，C0,3代入y=x2+bx+c，得
1+b+c=0c=3
解得：b=−4c=3
∴抛物线解析式为y=x2−4x+3；
（2）∵y=x2−4x+3 =x−22−1，
顶点坐标为2,1，
当y=0时，x2−4x+3=0
解得：x1=1,x2=3
∴A3,0，则OA=3
∵C0,3，则OC=3
∴△AOC是等腰直角三角形，
∵S△PAC=S△ABC
∴P到AC的距离等于B到AC的距离，
∵A3,0，C0,3，设直线AC的解析式为y=kx+3
∴3k+3=0
解得：k=−1
∴直线AC的解析式为y=−x+3，
如图所示，过点B作AC的平行线，交抛物线于点P，

设BP的解析式为y=−x+d，将点B1,0代入得，
−1+d=0
解得：d=1
∴直线BP的解析式为y=−x+1，
y=−x+1y=x2−4x+3
解得：x=1y=0或x=2y=−1
∴P2,−1，
∵PA=3−22+12=2,PB=2−12+12=2,AB=3−1=2
∴PA2+PB2=AB2
∴△ABP是等腰直角三角形，且∠APB=90°，
如图所示，延长PA至D，使得AD=PA，过点D作AC的平行线DE，交x轴于点E，则DA=PA，则符合题意的点P在直线DE上，
∵△APB是等腰直角三角形，DE∥AC,AC⊥PD
∴∠DAE=∠BAP=45° PD⊥DE
∴△ADE是等腰直角三角形，
∴AE=2AD=2AP=2
∴E5,0
设直线DE的解析式为y=−x+e
∴−5+e=0
解得：e=5
∴直线DE的解析式为y=−x+5
联立y=−x+5y=x2−4x+3
解得：x=3−172y=7+172或x=3+172y=7−172
∴P3−172,7+172或P3+172,7−172
综上所述，P2,−1或P3−172,7+172或P3+172,7−172；
（3）①当a>0时，如图所示，过点C作CG⊥AC交x=2于点G，
当点Q与点G重合时，△ACQ是直角三角形，
当∠AQC=90°时，△ACQ是直角三角形，

设AC交x=2于点H，
∵直线AC的解析式为y=−x+3，
则H2,1，
∴CH=22+3−12=22,
∵∠CHG=∠OCH=45°，
∴△CHG是等腰直角三角形，
∴HG=2CH =2×22=4
∴G2,5，
设Q2,q，则AQ2=12+q2,CQ2=22+q−32=q2−6q+13
∵AC2=32+32=18
∴18=q2−6q+13+12+q2
解得：q=3−172（舍去）或q=3+172
∴Q2,3+172
∵△QAC是锐角三角形
∴3+172当a<0时，如图所示，
同理可得AQ2+QC2=AC2
即∴18=q2−6q+13+12+q2
解得：q=3−172或q=3+172（舍去）
由（2）可得AM⊥AC时，M2,−1

∴−1综上所述，当△QAC是锐角三角形时，3+172【点睛】本题考查了二次函数综合运用，面积问题，角度问题，熟练掌握二次函数的性质是解题的关键．
2．（2023·四川甘孜·中考真题）已知抛物线y=x2+bx+c与x轴相交于A−1，0，B两点，与y轴相交于点C0，−3．

(1)求b，c的值；
(2)P为第一象限抛物线上一点，△PBC的面积与△ABC的面积相等，求直线AP的解析式；
(3)在（2）的条件下，设E是直线BC上一点，点P关于AE的对称点为点P'，试探究，是否存在满足条件的点E，使得点P'恰好落在直线BC上，如果存在，求出点P'的坐标；如果不存在，请说明理由．
【答案】(1)b=−2,c=−3.
(2)y=x+1
(3)存在，点P'的坐标为1+21,−2+21或1−21,−2−21
【分析】（1）由待定系数法即可求解；
（2）S△PBC=S△ABC得到AP∥BC，即可求解；
（3）由题意的：∠AEP=∠AEP',P'E=PE，即可求解．
【详解】（1）由题意，得1−b+c=0,c=−3.
∴b=−2,c=−3.
（2）由（1）得抛物线的解析式为y=x2−2x−3．
令y=0，则x2−2x−3=0，得x1=−1，x2=3．
∴B点的坐标为3，0．
∵S△PBC=S△ABC，
∴AP∥BC．
∵B3，0，C0，−3，
∴直线BC的解析式为y=x−3．
∵AP∥BC，
∴可设直线AP的解析式为y=x+m．
∵A（−1，0）在直线AP上，
∴0=−1+m．
∴m=1．
∴直线AP的解析式为y=x+1．

（3）设P点坐标为m，n．
∵点P在直线y=x+1和抛物线y=x2−2x−3上，
∴n=m+1，n=m2−2m−3．
∴m+1=m2−2m−3．
解得m1=4，m2=−1（舍去）．
∴点P的坐标为4，5．

由翻折，得∠AEP=∠AEP',P'E=PE．
∵AP∥BC，
∴∠PAE=∠AEP''．
∴∠PAE=∠PEA．
∴PE=PA=4+12+5−02=52．
设点E的坐标为t，t−3，则PE2=t−42+t−3−52=522．
∴t=6±21．
当t=6+21时，点E的坐标为6+21,3+21．
设P'(s,s−3),
由P'E=AP，P'E=PE=52得：
s−6−212+s−3−3−212=522，
解得：s=1+21，
则点P'的坐标为1+21,−2+21．
当t=6−21时，同理可得，点P'的坐标为1−21,−2−21．
综上所述，点P'的坐标为1+21,−2+21或1−21,−2−21．
【点睛】本题是二次函数的综合题，主要考查了用待定系数法求一次函数、二次函数的解析式，二次函数的性质，此题题型较好，综合性比较强，用的数学思想是分类讨论和数形结合的思想．
类型四 面积最值问题
题目要求：在抛物线上的第一象限找一点P，使S△PBC面积最大
方法简介：
方法一：S=12•水平宽•铅垂高
方法二：作l//BC，l与抛物线只有一个交点P，此时h最大，S△PBC面积最大，联立l与抛物线，△=0
1（2022·广东·中考真题）如图，抛物线y=x2+bx+c（b，c是常数）的顶点为C，与x轴交于A，B两点，A1,0，AB=4，点P为线段AB上的动点，过P作PQ//BC交AC于点Q．
(1)求该抛物线的解析式；
(2)求△CPQ面积的最大值，并求此时P点坐标．
【答案】(1)y=x2+2x−3
(2)2；P（-1，0）
【分析】（1）用待定系数法将A，B的坐标代入函数一般式中，即可求出函数的解析式；
（2）分别求出C点坐标，直线AC，BC的解析式，PQ的解析式为：y=-2x+n，进而求出P，Q的坐标以及n的取值范围，由S△CPQ=S△CPA−S△APQ列出函数式求解即可．
【详解】（1）解：∵点A（1，0），AB=4，
∴点B的坐标为（-3，0），
将点A（1，0），B（-3，0）代入函数解析式中得：
{0=1+b+c0=9−3b+c，
解得：b=2，c=-3，
∴抛物线的解析式为y=x2+2x−3；
（2）解：由（1）得抛物线的解析式为y=x2+2x−3，
顶点式为：y=(x+1)2−4，
则C点坐标为：（-1，-4），
由B（-3，0），C（-1，-4）可求直线BC的解析式为：y=-2x-6，
由A（1，0），C（-1，-4）可求直线AC的解析式为：y=2x-2，
∵PQ∥BC，
设直线PQ的解析式为：y=-2x+n，与x轴交点P(n2,0)，
由{y=−2x+ny=2x−2解得：Q(n+24,n−22)，
∵P在线段AB上，
∴−3∴n的取值范围为-6＜n＜2，
则S△CPQ=S△CPA−S△APQ
=12×(1−n2)×4−12×(1−n2)×(−n−22)
=−18(n+2)2+2
∴当n=-2时，即P（-1，0）时，S△CPQ最大，最大值为2．
【点睛】本题考查二次函数的面积最值问题，二次函数的图象与解析式间的关系，一次函数的解析式与图象，熟练掌握数形结合思想是解决本题的关键．
2．（2023·湖南娄底·中考真题）如图，抛物线y=x2+bx+c过点A−1,0、点B5,0，交y轴于点C．

(1)求b，c的值．
(2)点Px0,y00①当x0取何值时，△PBC的面积最大？并求出△PBC面积的最大值；
②过点P作PE⊥x轴，交BC于点E，再过点P作PF∥x轴，交抛物线于点F，连接EF，问：是否存在点P，使△PEF为等腰直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】(1)b=−4，c=−5
(2)①当x0=52时，△PBC的面积由最大值，最大值为1258；
②当点P的坐标为7−332,3−3332或4,−5时，△PEF为等腰直角三角形
【分析】（1）将将A−1,0、B5,0代入抛物线y=x2+bx+c即可求解；
（2）①由（1）可知：y=x2−4x−5，得C0,−5，可求得BC的解析式为y=x−5，过点P作PE⊥x轴，交BC于点E，交x轴于点Q，易得PE=yE−y0=−x02+5x0，根据△PBC的面积=S△PEC+S△PEB，可得△PBC的面积=12PE⋅x0−xC+12PE⋅xB−x0 =−52x0−522+1258，即可求解；
②由题意可知抛物线的对称轴为x对=−−42×1=2，则xF=4−x0，分两种情况：当点P在对称轴左侧时，即0【详解】（1）解：将A−1,0、B5,0代入抛物线y=x2+bx+c中，
可得：1−b+c=025+5b+c=0，解得：b=−4c=−5，
即：b=−4，c=−5；
（2）①由（1）可知：y=x2−4x−5，
当x=0时，y=−5，即C0,−5，
设BC的解析式为：y=kx+b，
将B5,0，C0,−5代入y=kx+b中，
可得5k+b=0b=−5，解得：k=1b=−5，
∴BC的解析式为：y=x−5，
过点P作PE⊥x轴，交BC于点E，交x轴于点Q，

∵Px0,y00∴点E的横坐标也为x0，则纵坐标为yE=x0−5，
∴PE=yE−y0=x0−5−x02−4x0−5=−x02+5x0，
△PBC的面积=S△PEC+S△PEB
=12PE⋅x0−xC+12PE⋅xB−x0
=12PE⋅xB−xC
=52−x02+5x0
=−52x0−522+1258，
∵−52<0，
∴当x0=52时，△PBC的面积有最大值，最大值为1258；
②存在，当点P的坐标为7−332,3−3332或4,−5时，△PEF为等腰直角三角形．
理由如下：由①可知PE=−x02+5x0，
由题意可知抛物线的对称轴为直线x对=−−42×1=2，
∵PF∥x轴，
∴∠EPF=90°，x0+xF2=x对=2，则xF=4−x0，
当点P在对称轴左侧时，即0
PF=xF−x0=4−2x0，当PE=PF时，△PEF为等腰直角三角形，
即：−x02+5x0=4−2x0，整理得：x02−7x0+4=0，
解得：x0=7−332（x0=7+332>2，不符合题意，舍去）
此时y0=x02−4x0−5=3−3332，即点P7−332,3−3332；
当点P在对称轴右侧时，即2
PF=x0−xF=2x0−4，当PE=PF时，△PEF为等腰直角三角形，
即：−x02+5x0=2x0−4，整理得：x02−3x0−4=0，
解得：x0=4（x0=−1<2，不符合题意，舍去）
此时：y0=42−4×4−5=−5，即点P4,−5；
综上所述，当点P的坐标为7−332,3−3332或4,−5时，△PEF为等腰直角三角形．
【点睛】本题二次函数综合题，考查了利用待定系数法求函数解析式，二次函数的性质及图象上的点的特点，等腰直角三角形的性质，解本题的关键是表示出点的坐标，进行分类讨论．
3．（2023·辽宁阜新·中考真题）如图，在平面直角坐标系中，二次函数y=−x2+bx−c的图象与x轴交于点A(−3,0)和点B(1,0)，与y轴交于点C．

(1)求这个二次函数的表达式．
(2)如图1，二次函数图象的对称轴与直线AC:y=x+3交于点D，若点M是直线AC上方抛物线上的一个动点，求△MCD面积的最大值．
(3)如图2，点P是直线AC上的一个动点，过点P的直线l与BC平行，则在直线l上是否存在点Q，使点B与点P关于直线CQ对称？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
【答案】(1)y=−x2−2x+3；
(2)S△MCD最大=98；
(3)Q1−5，−5或1+5，5．
【分析】
（1）根据抛物线的交点式直接得出结果；
（2）作MQ⊥AC于Q，作ME⊥AB于F，交AC于E，先求出抛物线的对称轴，进而求得C，D坐标及CD的长，从而得出过M的直线y=x+m与抛物线相切时，△MCD的面积最大，根据x+m=−x2−2x+3的△=0求得m的值，进而求得M的坐标，进一步求得CD上的高MQ的值，进一步得出结果；
（3）分两种情形：当点P在线段AC上时，连接BP，交CQ于R，设P(t，t+3)，根据CP=CB求得t的值，可推出四边形BCPQ是平行四边形，进而求得Q点坐标；当点P在AC的延长线上时，同样方法得出结果．
【详解】（1）
解：由题意得，
y=−(x+3)(x−1)=−x2−2x+3；
（2）
解：如图1，
作MQ⊥AC于Q，作ME⊥AB于F，交AC于E，
∵OA=OC=3，∠AOC=90°，
∴∠CAO=∠ACO=45°，
∴∠MEQ=∠AEF=90°−∠CAO=45°，
抛物线的对称轴是直线：x=−3+12=−1，
∴y=x+3=−1+3=2，
∴D(1,2)，
∵C(0,3)，
∴CD=2，
故只需△MCD的边CD上的高最大时，△MCD的面积最大，
设过点M与AC平行的直线的解析式为：y=x+m，
当直线y=x+m与抛物线相切时，△MCD的面积最大，
由x+m=−x2−2x+3得，
x2+3x+(m−3)=0，
由△=0得，
32−4(m−3)=0得，
m−3=94，
∴x2+3x+94=0，
∴x1=x2=−32，
∴y=−−322−2×−32+3=154，
y=x+3=−32+3=32，
∴ME=154−32=94，
∴MQ=ME⋅sin∠MEQ=ME⋅sin45°=94×22=928，
∴S△MCD最大=12×2×928=98；
（3）
解：如图2，
当点P在线段AC上时，连接BP，交CQ于R，
∵点B和点Q关于CQ对称，
∴CP=CB，
设P(t，t+3)，
由CP2=CB2得，2t2=10，
∴t1=−5，t2=5（舍去），
∴P−5，3−5，
∵PQ∥BC，
∴ CRQR=BRPR=1，
∴CR=QR，
∴四边形BCPQ是平行四边形，
∵1+(−5)−0=1−5，0+(3−5)−3=−5，
∴Q1−5，−5；
如图3，
当点P在AC的延长线上时，由上可知：P5，3+5，
同理可得：Q1+5，5，
综上所述：Q1−5，−5或1+5，5．
【点睛】
本题考查了二次函数及其图象的性质，一元二次方程的解法，平行四边形的判定和性质，轴对称的性质等知识，解决问题的关键是分类讨论．
题型02 线段相关问题
对于阿氏圆而言：当系数k＜1的时候，一般情况下，考虑向内构造.
当系数k＞1的时候，一般情况下，考虑向外构造.
【注意事项】针对求PA+kPB的最小值问题时，当轨迹为直线时，运用“胡不归模型”求解；
当轨迹为圆形时，运用“阿氏圆模型”求解.
类型一 线段和最小问题
1．（2023·山东枣庄·中考真题）如图，抛物线y=−x2+bx+c经过A(−1,0),C(0,3)两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．

(1)求该抛物线的表达式；
(2)若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；
(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．
【答案】(1)y=−x2+2x+3
(2)37
(3)存在，Q1,3或Q1,1或Q1,5
【分析】
（1）待定系数法求出函数解析式即可；
（2）作点D关于x轴的对称点D'，连接D'M，D'M与x轴的交点即为点H，进而得到MH+DH的最小值为D'M的长，利用两点间距离公式进行求解即可；
（3）分DM，DP，MP分别为对角线，三种情况进行讨论求解即可．
【详解】（1）解：∵抛物线y=−x2+bx+c经过A(−1,0),C(0,3)两点，
∴−1−b+c=0c=3，解得：b=2c=3，
∴y=−x2+2x+3；
（2）∵y=−x2+2x+3=−x−12+4，
∴M1,4，
设直线AM:y=kx+m(k≠0)，
则：−k+m=0k+m=4，解得：k=2m=2，
∴AM:y=2x+2，
当x=0时，y=2，
∴D0,2；
作点D关于x轴的对称点D'，连接D'M，
则：D'0,−2，MH+DH=MH+D'H≥D'M，
∴当M,H,D'三点共线时，MH+DH有最小值为D'M的长，

∵D'0,−2，M1,4，
∴D'M=12+4+22=37，
即：MH+DH的最小值为：37；
（3）解：存在；
∵y=−x2+2x+3=−x−12+4，
∴对称轴为直线x=1，
设Pp,t，Q1,n，
当以D，M，P，Q为顶点的四边形是平行四边形时：
①DM为对角线时：1+p=0+1t+n=4+2，

∴p=0t+n=6，
当p=0时，t=3，
∴n=3，
∴Q1,3；
②当DP为对角线时：0+p=1+12+t=4+n，

∴p=22+t=4+n，
当p=2时，t=−22+2×2+3=3，
∴n=1，
∴Q1,1；
③当MP为对角线时：1+p=0+14+t=2+n，

∴p=0n−t=2，
当p=0时，t=3，
∴n=5，
∴Q1,5；
综上：当以D，M，P，Q为顶点的四边形是平行四边形时，Q1,3或Q1,1或Q1,5．
【点睛】
本题考查二次函数的综合应用，是中考常见的压轴题．正确的求出函数解析式，熟练掌握二次函数的性质，利用数形结合和分类讨论的思想进行求解，是解题的关键．
2．（2023·宁夏·中考真题）如图，抛物线y=ax2+bx+3(a≠0)与x轴交于A，B两点，与y轴交于点C．已知点A的坐标是−1,0，抛物线的对称轴是直线x=1．

(1)直接写出点B的坐标；
(2)在对称轴上找一点P，使PA+PC的值最小．求点P的坐标和PA+PC的最小值；
(3)第一象限内的抛物线上有一动点M，过点M作MN⊥x轴，垂足为N，连接BC交MN于点Q．依题意补全图形，当MQ+2CQ的值最大时，求点M的坐标．
【答案】(1)3,0
(2)点P1,2，PA+PC的最小值为32
(3)M52,74
【分析】（1）根据抛物线的对称性，进行求解即可；
（2）根据抛物线的对称性，得到PA+PC=PB+PC≥BC，得到当P,B,C三点共线时，PA+PC的值最小，为BC的长，求出直线BC的解析式，解析式与对称轴的交点即为点P的坐标，两点间的距离公式求出BC的长，即为PA+PC的最小值；
（3）根据题意，补全图形，设Mm,−m2+2m+3，得到Nm,0，Qm,−m+3，将MQ+2CQ的最大值转化为二次函数求最值，即可得解．
【详解】（1）解：∵点A−1,0关于对称轴的对称点为点B，对称轴为直线x=1，
∴点B为3,0；
（2）当x=0时，y=3，
∴C0,3，
连接BC，

∵B3,0，
∴BC=32+32=32，
∵点A关于对称轴的对称点为点B，
∴PA+PC=PB+PC≥BC，
∴当P,B,C三点共线时，PA+PC的值最小，为BC的长，
设直线BC的解析式为：y=kx+n，
则：n=33k+n=0，解得：n=3k=−1，
∴y=−x+3，
∵点P在抛物线的对称轴上，
∴P1,2；
∴点P1,2，PA+PC的最小值为32；
（3）过点M作MN⊥x轴，垂足为N，连接BC交MN于点Q，如图所示，

∵A−1,0,B3,0，
设抛物线的解析式为：y=ax+1x−3，
∵C0,3，
∴3=−3a，
∴a=−1，
∴y=−x+1x−3=−x2+2x+3，
设Mm,−m2+2m+3，则：Nm,0，
由（2）知：直线BC：y=−x+3，
∴Qm,−m+3，
∴MQ=−m2+2m+3+m−3=−m2+3m，
∵C0,3,B3,0，
∴OC=OB=3，BN=3−m，
∴∠OBC=∠OCB=45°，
∴∠NQB=∠OBC=45°，
∴BQ=2BN=23−m，
∴CQ=BC−BQ=32−32+2m=2m，
∴MQ+2CQ=−m2+3m+2⋅2m=−m2+5m=−m−522+254，
∴当m=52时，MQ+2CQ有最大值，此时M52,74．
【点睛】本题考查二次函数的综合应用．正确的求出函数解析式，利用抛物线的对称性以及数形结合的思想进行求解，是解题的关键．
类型二 周长最值问题
1．（2023·湖南郴州·中考真题）已知抛物线y=ax2+bx+4与x轴相交于点A1,0，B4,0，与y轴相交于点C．
(1)求抛物线的表达式；
(2)如图1，点P是抛物线的对称轴l上的一个动点，当△PAC的周长最小时，求PAPC的值；
(3)如图2，取线段OC的中点D，在抛物线上是否存在点Q，使tan∠QDB=12？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】(1)y=x2−5x+4
(2)35
(3)Q5+172,2或Q5−172,2或Q3,−2或Q23,109
【分析】
（1）待定系数法求函数解析式即可；
（2）根据△PAC的周长等于PA+PC+AC，以及AC为定长，得到当PA+PC的值最小时，△PAC的周长最小，根据抛物线的对称性，得到A,B关于对称轴对称，则：PA+PC=PB+PC≥BC，得到当P,B,C三点共线时，PA+PC=BC，进而求出P点坐标，即可得解；
（3）求出D点坐标为0,2，进而得到tan∠OBD=12，得到∠QDB=∠OBD，分点Q在D点上方和下方，两种情况进行讨论求解即可．
【详解】（1）解：∵抛物线y=ax2+bx+4与x轴相交于点A1,0，B4,0，
∴a+b+4=016a+4b+4=0，解得：a=1b=−5，
∴y=x2−5x+4；
（2）∵y=x2−5x+4，当x=0时，y=4，
∴C0,4，抛物线的对称轴为直线x=52
∵△PAC的周长等于PA+PC+AC，AC为定长，
∴当PA+PC的值最小时，△PAC的周长最小，
∵A,B关于对称轴对称，
∴PA+PC=PB+PC≥BC，当P,B,C三点共线时，PA+PC的值最小，为BC的长，此时点P为直线BC与对称轴的交点，
设直线BC的解析式为：y=mx+n，
则：4m+n=0n=4，解得：m=−1n=4，
∴y=−x+4，
当x=52时，y=−52+4=32，
∴P52,32，
∵A1,0,C0,4，
∴PA=52−12+322=322，PC=522+4−322=522，
∴PAPC=35；
（3）解：存在，
∵D为OC的中点，
∴D0,2，
∴OD=2，
∵B4,0，
∴OB=4，
在Rt△BOD中，tan∠OBD=ODOB=12，
∵tan∠QDB=12=tan∠OBD，
∴∠QDB=∠OBD，
①当Q点在D点上方时：
过点D作DQ∥OB，交抛物线与点Q，则：∠QDB=∠OBD，此时Q点纵坐标为2，
设Q点横坐标为t，
则：t2−5t+4=2，
解得：t=5±172，
∴Q5+172,2或Q5−172,2；
②当点Q在D点下方时：设DQ与x轴交于点E，
则：DE=BE，
设Ep,0，
则：DE2=OE2+OD2=p2+4，BE2=4−p2，
∴p2+4=4−p2，解得：p=32，
∴E32,0，
设DE的解析式为：y=kx+q，
则：q=23k2+q=0，解得：q=2k=−43，
∴y=−43x+2，
联立y=−43x+2y=x2−5x+4，解得：x=3y=−2或x=23y=109，
∴Q3,−2或Q23,109；
综上：Q5+172,2或Q5−172,2或Q3,−2或Q23,109．
【点睛】本题考查二次函数的综合应用，正确的求出二次函数解析式，利用数形结合，分类讨论的思想进行求解，是解题的关键．本题的综合性强，难度较大，属于中考压轴题．
2．（2022·山东东营·中考真题）如图，抛物线y=ax2+bx−3(a≠0)与x轴交于点A(−1,0)，点B(3,0)，与y轴交于点C．
(1)求抛物线的表达式；
(2)在对称轴上找一点Q，使△ACQ的周长最小，求点Q的坐标；
(3)点P是抛物线对称轴上的一点，点M是对称轴左侧抛物线上的一点，当△PMB是以PB为腰的等腰直角三角形时，请直接写出所有点M的坐标．
【答案】(1)y=x2−2x−3
(2)（1，-2）
(3)（-1，0）或（1−2，-2）或（1−6，2）
【分析】（1）利用待定系数法求解即可；
（2）先求出点C的坐标和抛物线的对称轴，如图所示，作点C关于直线x=1的对称点E，连接AE，EQ，则点E的坐标为（2，-3），根据轴对称最短路径可知AE与抛物线对称轴的交点即为点Q；
（3）分两种情况当∠BPM=90°和当∠PBM=90°两种情况讨论求解即可．
【详解】（1）解：∵抛物线y=ax2+bx−3(a≠0)与x轴交于点A(−1,0)，点B(3,0)，
∴a−b−3=09a+3b−3=0，
∴a=1b=−2，
∴抛物线解析式为y=x2−2x−3；
（2）解：∵抛物线解析式为y=x2−2x−3=x−12−4，与y轴交于点C，
∴抛物线对称轴为直线x=1，点C的坐标为（0，-3）
如图所示，作点C关于直线x=1的对称点E，连接AE，EQ，则点E的坐标为（2，-3），
由轴对称的性质可知CQ=EQ，
∴△ACQ的周长=AC+AQ+CQ，
要使△ACQ的周长最小，则AQ+CQ最小，即AQ+QE最小，
∴当A、Q、E三点共线时，AQ+QE最小，
设直线AE的解析式为y=k1x+b1，
∴−k1+b1=02k1+b1=−3，
∴k1=−1b1=−1，
∴直线AE的解析式为y=−x−1，
当x=1时，y=−x−1=−1−1=−2，
∴点Q的坐标为（1，-2）；
（3）解： 如图1所示，当点P在x轴上方，∠BPM=90°时，过点P作EF∥x轴，过点M作MF⊥EF于F，过点B作BE⊥EF于E，
∵△PBM是以PB为腰的等腰直角三角形，
∴PA=PB，∠MFP=∠PEB=∠BPM=90°，
∴∠FMP+∠FPM=∠FPM+∠EPB=90°，
∴∠FMP=∠EPB，
∴△FMP≌△EPB（AAS），
∴PE=MF，BE=PF，
设点P的坐标为（1，m），
∴BE=m，PE=2，
∴MF=2，PF=m，
∴点M的坐标为（1-m，m-2），
∵点M在抛物线y=x2−2x−3上，
∴1−m2−21−m−3=m−2，
∴1−2m+m2−2+2m−3=m−2，
∴m2−m−2=0，
解得m=2或m=−1（舍去），
∴点M的坐标为（-1，0）；
同理当当点P在x轴下方，∠BPM=90°时可以求得点M的坐标为（-1，0）；
如图2所示，当点P在x轴上方，∠PBM=90°时，过点B作EF∥y轴，过点P作PE⊥EF于E，过点M作MF⊥EF于F，设点P的坐标为（1，m），
同理可证△PEB≌△BFM（AAS），
∴BF=PE=2，MF=BE=m，
∴点M的坐标为（3-m，-2），
∵点M在抛物线y=x2−2x−3上，
∴3−m2−23−m−3=−2，
∴9−6m+m2−6+2m−3=−2，
∴m2−4m+2=0，
解得m=2+2或m=2−2（舍去），
∴点M的坐标为（1−2，-2）；
如图3所示，当点P在x轴下方，∠PBM=90°时，
同理可以求得点M的坐标为（1−6，2）；
综上所述，当△PMB是以PB为腰的等腰直角三角形时，点M的坐标为（-1，0）或（1−2，-2）或（1−6，2）．
【点睛】本题主要考查了待定系数法求二次函数解析式，二次函数综合，一次函数与几何综合，全等三角形的性质与判定等等，熟知二次函数的相关知识是解题的关键．
3．（2022·广西柳州·中考真题）已知抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（m，0）两点，与y轴交于点C（0，5）．

(1)求b，c，m的值；
(2)如图1，点D是抛物线上位于对称轴右侧的一个动点，且点D在第一象限内，过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，垂足为点F，当四边形DEFG的周长最大时，求点D的坐标；
(3)如图2，点M是抛物线的顶点，将△MBC沿BC翻折得到△NBC，NB与y轴交于点Q，在对称轴上找一点P，使得△PQB是以QB为直角边的直角三角形，求出所有符合条件的点P的坐标．
【答案】(1)b=4，c=5， m=5
(2)当四边形DEFG的周长最大时，点D的坐标为（3，8）
(3)所有符合条件的点P的坐标为（2，233），（2，﹣9）
【分析】（1）把A（﹣1，0），C（0，5）代入y＝﹣x2+bx+c，利用待定系数法求解b，c即可，再令y=0，再解方程求解m即可；
（2）先求解抛物线的对称轴为x＝2，设D（x，﹣x2+4x+5），则E（4﹣x，﹣x2+4x+5），证明四边形DEFG是矩形，而DE=2x−4,DF=−x2+4x+5, 可得四边形DEFG的周长＝2（﹣x2+4x+5）+2（2x﹣4）＝﹣2x2+12x+2＝﹣2（x﹣3）2+20，再利用二次函数的性质可得答案；
（3）过点C作CH⊥对称轴于H，过点N作NK⊥y轴于K，证明△MCH≌△NCK（AAS），再求解N（﹣4，3），求解直线BN的解析式为：y=−13x+53, 可得Q(0,53), 设P（2，p），再利用勾股定理表示PQ2=22+(p−53)2=p2−103p+619, BP2＝(5−2)2+p2=9+p2，BQ2=52+(53)2=25+259, 再分两种情况建立方程求解即可．
【详解】（1）把A（﹣1，0），C（0，5）代入y＝﹣x2+bx+c，
∴{−1−b+c=0c=5 ，解得：{b=4c=5,
∴这个抛物线的解析式为：y＝﹣x2+4x+5，
令y＝0，则﹣x2+4x+5＝0，解得x1＝5，x2＝﹣1，
∴B（5，0），
∴m＝5；
（2）∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴对称轴为x＝2，
设D（x，﹣x2+4x+5），
∵DE∥x轴，
∴E（4﹣x，﹣x2+4x+5），
∵过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，
∴四边形DEFG是矩形，
∴DE=2x−4,DF=−x2+4x+5,
∴四边形DEFG的周长＝2（﹣x2+4x+5）+2（2x﹣4）＝﹣2x2+12x+2＝﹣2（x﹣3）2+20，
∴当x＝3时，四边形DEFG的周长最大，
∴当四边形DEFG的周长最大时，点D的坐标为（3，8）；
（3）过点C作CH⊥对称轴于H，过点N作NK⊥y轴于K，

∴∠NKC＝∠MHC＝90°，
由翻折得CN＝CM，∠BCN＝∠BCM，
∵B（5，0），C（0，5）．
∴OB＝OC，
∴∠OCB＝∠OBC＝45°，
∵CH⊥对称轴于H，
∴CH∥x轴，
∴∠BCH＝45°，
∴∠BCH＝∠OCB，
∴∠NCK＝∠MCH，
∴△MCH≌△NCK（AAS），
∴NK＝MH，CK＝CH，
∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴对称轴为x＝2，M（2，9），
∴MH＝9﹣5＝4，CH＝2，
∴NK＝MH＝4，CK＝CH＝2，
∴N（﹣4，3），
设直线BN的解析式为y＝mx+n，
∴{−4m+n=35m+n=0, 解得：{m=−13n=53,
∴直线BN的解析式为：y=−13x+53,
∴Q(0,53),
设P（2，p），
∴PQ2=22+(p−53)2=p2−103p+619,
BP2＝(5−2)2+p2=9+p2，
BQ2=52+(53)2=25+259,
分两种情况：
①当∠BQP＝90°时，BP2＝PQ2+BQ2，
∴9+p2=p2−103p+619+25+259,
解得：p=233,
∴P(2,233),
②当∠QBP＝90°时，P′Q2＝BP′2+BQ2，
∴p2−103p+619=9+p2+25+259,
解得：p=−9,
∴点P′的坐标为（2，﹣9）．
综上，所有符合条件的点P的坐标为(2,233)或P(2,−9)．
【点睛】本题考查的是利用待定系数法求解二次函数的解析式，二次函数与坐标轴的交点坐标问题，二次函数的性质，对称轴的性质，二次函数与直角三角形，勾股定理的应用，清晰的分类讨论是解本题的关键．
题型03 存在性问题
类型一 平行四边形存在性问题
平行四边形存在性问题通常可分为“三定一动”和“两定两动”两大类问题.而且“三定一动”的动点和“两定两动”的动点性质并不完全一样,“三定一动”中动点是在平面中横纵坐标都不确定，需要用两个字母表示，这样的我们姑且称为“全动点”，而有一些动点在坐标轴、直线或者抛物线上，用一个字母即可表示点坐标，称为“半动点”.找不同图形的存在性最多可以有几个未知量，都是根据图形决定的，像平行四边形，只能有2个未知量.究其原因，在于平行四边形两大性质:(1)对边平行且相等:(2)对角线互相平分. 但此两个性质统一成一个等式:xA+xC=xB+xDyA+yC=yB+yD，两个等式，只能允许最多存在两个未知数，即我们刚刚所讲的平行四边形存在性问题最多只能存在2个未知量. 由图形性质可知未知量，由未知量可知动点设计，由动点设计可化解问题.
1．（2023·山东淄博·中考真题）如图，一条抛物线y=ax2+bx经过△OAB的三个顶点，其中O为坐标原点，点A3,−3，点B在第一象限内，对称轴是直线x=94，且△OAB的面积为18

(1)求该抛物线对应的函数表达式；
(2)求点B的坐标；
(3)设C为线段AB的中点，P为直线OB上的一个动点，连接AP，CP，将△ACP沿CP翻折，点A的对应点为A1．问是否存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
【答案】(1)y=23x2−3x
(2)6,6
(3)存在，P点的坐标为32，32或−32，−32或352+6，352+6或−352+6，−352+6
【分析】（1）根据对称轴为直线x=−b2a=94，将点A代入，进而待定系数法求解析式即可求解；
（2）设Bm,23m2−3m，过点A作EF⊥y轴交于E点，过B点作BF⊥EF交于F点，继而表示出△OAB的面积，根据△OAB的面积为18，解方程，即可求解．
（3）先得出直线OB的解析式为y=x，设Pt,t，当BP为平行四边形的对角线时，可得AP=AC，当BC为平行四边形的对角线时，BP=AC，进而建立方程，得出点P的坐标，即可求解．
【详解】（1）解：∵对称轴为直线x=−b2a=94，
∴b=−92a①，
将点A3,−3代入y=ax2+bx得，
∴9a+3b=−3②，
联立①②得，a=23b=−3，
∴解析式为y=23x2−3x；
（2）设Bm,23m2−3m，如图所示，过点A作EF⊥y轴交于E点，过B点作BF⊥EF交于F点，

∴Fm,−3，E0,−3，
则OE=3,AE=3,AF=m−3,BF=23m2−3m+3，
∴S△AOB=12m×23m2−3m+3+3−12×3×3−12m−323m2−3m+3=18
解得：m=6或m=−3（舍去），
（3）存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形，理由如下：
∵A3,−3,B6,6，
∴C92,32，
设直线OB的解析式为y=kx，
∴6k=6，解得：k=1，
∴直线OB的解析式为y=x，
设Pt,t，
如图所示，当BP为平行四边形的对角线时，BC∥A1P，

BC=A1P，
∵AC=BC，
∴AC=A1P，
由对称性可知AC=A1C，AP=A1P，
∴AP=AC，
∴t−32+t+32=3−922+−3−322
解得：t=±32
∴P点的坐标为32，32或−32，−32
如图3，当BC为平行四边形的对角线时，BP∥A1C，BP=A1C，

由对称性可知，AC=A1C，
∴BP=AC，
∴6−t2+6−t2=3−922+−3−322，
解得：t=352+6或t=−352+6，
∴P点的坐标为352+6，352+6或−352+6，−352+6
综上所述，P点的坐标为32，32或−32，−32或352+6，352+6或−352+6，−352+6．
【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，平行四边形的性质，轴对称的性质是解题的关键．
2．（2022·四川攀枝花·中考真题）如图，二次函数y=ax2+bx+c的图象与x轴交于O（O为坐标原点），A两点，且二次函数的最小值为−1，点M(1,m)是其对称轴上一点，y轴上一点B(0,1)．

(1)求二次函数的表达式；
(2)二次函数在第四象限的图象上有一点P，连结PA，PB，设点P的横坐标为t，△PAB的面积为S，求S与t的函数关系式；
(3)在二次函数图象上是否存在点N，使得以A、B、M、N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点N的坐标，若不存在，请说明理由．
【答案】(1)y=x2−2x
(2)S=−t2+32t+1
(3)存在，N(1,−1)或(3,3)或(−1,3)
【分析】（1）由二次函数的最小值为−1，点M(1,m)是其对称轴上一点，得二次函数顶点为(1,−1)，设顶点式y=a(x−1)2−1，将点O(0,0)代入即可求出函数解析式；
（2）连接OP，根据S=S△AOB+S△OAP−S△OBP求出S与t的函数关系式；
（3）设Nn,n2−2n，分三种情况：当AB为对角线时，当AM为对角线时，当AN为对角线时，由中点坐标公式求出n即可．
【详解】（1）解：∵二次函数的最小值为−1，点M(1,m)是其对称轴上一点，
∴二次函数顶点为(1,−1)，
设二次函数解析式为y=a(x−1)2−1，
将点O(0,0)代入得，a−1=0，
∴a=1，
∴y=(x−1)2−1=x2−2x；
（2）如图，连接OP，

当y=0时，x2−2x=0，
∴x=0或2，∴A(2,0)，
∵点P在抛物线y=x2−2x上，
∴点P的纵坐标为t2−2t，
∴S=S△AOB+S△OAP−S△OBP
=12×2×1+12×2−t2+2t−12t
=−t2+32t+1；
（3）设Nn,n2−2n，
当AB为对角线时，由中点坐标公式得，2+0=1+n，∴n=1，∴N(1,−1)，
当AM为对角线时，由中点坐标公式得，2+1=n+0，∴n=3，∴N(3,3)，
当AN为对角线时，由中点坐标公式得，2+n=0+1，∴n=−1，∴N(−1,3)，
综上：N(1,−1)或(3,3)或(−1,3)．
【点睛】此题考查了待定系数法求抛物线的解析式，抛物线与图形面积，平行四边形的性质，熟练掌握待定系数法及平行四边形是性质是解题的关键．
类型二 矩形存在性问题
矩形除了具有平行四边形的性质之外，还有“对角线相等”或“内角为直角”，因此相比起行四边形，坐标系中的矩形满足以下3个等式:xA+xC=xB+xDyA+yC=yB+yD（xA−xC）2+（yA−yC）2=（xB−xD）2+（yB−yD）2 (AC 为对角线时).因此在矩形存在性问题最多可以有3个未知量，代入可以得到三元一次方程组，可解确定了有3个未知量，则可判断常见矩形存在性问题至少有2个动点，多则可以有3个.
1（2023·海南·中考真题）如图1，抛物线y=x2+bx+c交x轴于A，B3,0两点，交y轴于点C0,−3．点P是抛物线上一动点．

(1)求该抛物线的函数表达式；
(2)当点P的坐标为1,−4时，求四边形BACP的面积；
(3)当动点P在直线BC上方时，在平面直角坐标系是否存在点Q，使得以B，C，P，Q为顶点的四边形是矩形？若存在，请求出点Q的坐标；若不存在，请说明理由；
(4)如图2，点D是抛物线的顶点，过点D作直线DH∥y轴，交x轴于点H，当点P在第二象限时，作直线PA，PB分别与直线DH交于点G和点I，求证：点D是线段IG的中点．
【答案】(1)y=x2−2x−3
(2)9
(3)在平面直角坐标系内存在点Q，使得以B、C、P、Q为顶点的四边形是矩形，此时点Q的坐标为−5,2或5+52,−1−52
(4)证明过程见解析
【分析】
（1）利用待定系数法求解即可；
（2）连接OP，过点P作PE⊥AB于点E，利用点的坐标表示出线段OA、OB、OC、OE、PE的长度，再根据S四边形BACP=S△OAC+S△OCP+S△OBP，进行计算即可；
（3）当BC为矩形的边时，画出符合题意的矩形，PB交y轴于点E，CQ交x轴于点F，连接EF，过点P作PM⊥y轴于点M，过点Q作QN⊥x轴于点N，利用等腰直角三角形的判定与性质及矩形的判定与性质得到NF=QN=PM=ME，利用待定系数法求得直线PB的解析式与抛物线的解析式联立方程组求得点P的坐标，则PM=2，进而得到ON、QN的长度，即可得出结果；当BC为对角线时，画出相应的图形，求出结果即可；
（4）利用配方法求得抛物线的顶点坐标、对称轴，再利用待定系数法求得直线PA、PB的解析式，进而求得点I、G的坐标，利用点的坐标表示出线段ID、GD的长度，即可得出结论．
【详解】（1）解：由题意可得，c=−30=9+3b+c，
解得b=−2c=−3，
∴抛物线的解析式为y=x2−2x−3；
（2）解：连接OP，过点P作PE⊥AB于点E，如图，
∵点P的坐标为1,−4，
∴PE=4，OE=1，
令y=0，则x2−2x−3=0，
解得x=3或x=1，
∴A−1,0，
∴OA=1，
∵C0,−3，B3,0，
∴OC=3，OB=3，
∴S四边形BACP=S△OAC+S△OCP+S△OBP，
=12OA⋅OC+12OC⋅OE+12OB⋅PE
=12×1×3+12×3×1+12×3×4
=9；
（3）解：在平面直角坐标系内存在点Q，使得以B、C、P、Q为顶点的四边形是矩形，理由如下：
如图，当BC为边时，四边形BCQP为符合条件的矩形，PB交y轴于点E，CQ交x轴于点F，连接EF，过点P作PM⊥y轴于点M，过点Q作QN⊥x轴于点N，
∵OC=OB=3，
∴∠OBC=∠OCB=45°，
∵四边形BCQP为矩形，
∴∠PBC=∠QCB=90°，
∴∠OBE=∠OCF=45°，
∴△OBE和△OCF为等腰直角三角形，
∴OB=OC=OE=OF=3，
∵四边形BCFE为正方形，
∴CF=BE，∠EFC=∠BEF=90°，
∴四边形EFQP为矩形，
∴QF=PE，
∵∠MEP=∠BEO=45°，∠QFN=∠OFC=45°，
∴△PME和△QNF为全等的等腰直角三角形，
∴NF=QN=PM=ME，
∵OE=3，
∴E0,3，
设直线BE的解析式为y=kx+nk≠0，
∴3k+n=0n=3，
∴k=−1n=3，
∴直线BE的解析式为y=−x+3，
联立方程组得y=−x+3y=x2−2x−3，
解得x=3y=0或x=−2y=5，
∴P−2,5，
∴PM=2，
∴QN=NF=2，
∴ON=OF+NF=3+2=5，
∴Q−5,2；
如图，当BC为对角线时，四边形BPCQ为矩形，过点Q作QD⊥x轴于点D，PE⊥x轴于点E，
则∠PEB=∠BDQ=90°，∠PBQ=90°，
∵∠PBE+∠EPB=∠PBE+∠DBQ=90°，
∴∠EPB=∠DBQ，
∴△BEP∽△QDB，
∴PEDB=BEDQ，
设点P的坐标为：t,t2−2t−3t<0或t>3，QxQ，yQ，
∵C0,−3，B3,0，
∴xQ=3−t，yQ=−t2+2t，
∴Q3−t,−t2+2t，
∴DQ=t2−2t，BD=−t，EP=−t2+2t+3，BE=3−t，
∴−t2+2t+3−t=3−tt2−2t，
整理得：t3−4t2+2t+3=0，
分解因式得：t−3t2−t−1=0，
解得：t1=3（舍去），t2=1+52<3（舍去），t3=1−52<0，
∴此时点Q的坐标为：5+52,−1−52．
综上所述，在平面直角坐标系内存在点Q，使得以B、C、P、Q为顶点的四边形是矩形，此时点Q的坐标为−5,2或5+52,−1−52；
（4）证明：∵y=x2−2x−3=x−12−4，
∴抛物线y=x2−2x−3的顶点D的坐标为1,−4，对称轴为直线x=1，
设Pm,m2−2m−3，直线PB的解析式为y=cx+dc≠0，
∴cm+d=m2−2m−33c+d=0，
∴c=m+1d=−3m−3，
∴直线PB的解析式为y=m+1x−3m−3，
当x=1时，y=−2m−2，
∴I1,−2m−2，
∴ID=−2m−2−−4=−2m+2，
设直线PA的解析式为y=ex+fe≠0，
∴em+f=m2−2m−3−e+d=0，
∴e=m−3f=m−3，
∴直线PA的解析式为y=m−3x+m−3，
当x=1时，y=2m−6，
∴G1,2m−6，
∴DG=−4−2m−6=−2m+2，
∴ID=DG，
∴点D是线段IG的中点．
【点睛】本题考查二次函数的图象与性质、用待定系数法求函数解析式、二次函数图象上点的坐标特征、一次函数的性质、一次函数图象上点的坐标特征、等腰直角三角形的判定与性质、矩形的判定与性质，利用点的坐标表示出相应线段的长度是解题的关键．
2．（2023·内蒙古·中考真题）如图，在平面直角坐标系中，抛物线y=−x2+bx+c与x轴的交点分别为A和B1,0（点A在点B的左侧），与y轴交于点C0,3，点P是直线AC上方抛物线上一动点．

(1)求抛物线的解析式；
(2)如图1，过点P作x轴平行线交AC于点E，过点P作y轴平行线交x轴于点D，求PE+PD的最大值及点P的坐标；
(3)如图2，设点M为抛物线对称轴上一动点，当点P，点M运动时，在坐标轴上确定点N，使四边形PMCN为矩形，求出所有符合条件的点N的坐标．
【答案】(1)y=−x2−2x+3
(2)PD+PE的最大值为498，点P的坐标为−54,6316
(3)符合条件的N点坐标为：N0,4或N1−1456,0
【分析】（1）利用待定系数法即可求解；
（2）先求得直线AC的解析式，设Pm,−m2−2m+3，则PE=−m2−3m，PD=−m2−2m+3，得到PD+PE=−2m+542+498，利用二次函数的性质求解即可；
（3）先求得抛物线的顶点P−1，4，对称轴为x=−1，分当点N在y轴上和点N在x轴负半轴上时，两种情况讨论，当点N在x轴负半轴上时，证明△CMG∽△NCO，求得CG=−13t，再证明△CMG≌△PNH，求得点P的坐标为t−1,−13t，由点P在抛物线上，列式计算求解即可．
【详解】（1）解：∵抛物线y=−x2+bx+c与x轴交于点B(1,0)，与y轴交于点C(0,3)
−1+b+c=0c=3
解得b=−2c=3
抛物线的解析式为：y=−x2−2x+3；
（2）解：当y=0时，0=−x2−2x+3，
解得x1=−3，x2=1，
∴A(−3,0)，
设直线AC的解析式为：y=kx+nk≠0，
把A−3,0，C0,3代入得：−3k+n=0n=3，
解得k=1n=3
∴直线AC的解析式为y=x+3，

设Pm,−m2−2m+3，
∵PE∥x轴，
∴点E的纵坐标为−m2−2m+3，
又∵点E在直线AC上，
∴−m2−2m+3=x+3，x=−m2−2m，
∴E−m2−2m,−m2−2m+3，
∴PE=−m2−2m−m=−m2−3m，
∵PD∥y轴，
∴PD=−m2−2m+3，
∴PD+PE=−m2−2m+3+−m2−3m=−2m2−5m+3=−2m+542+498，
∵−2<0，−3∴当m=−54时，PD+PE有最大值，最大值为498，
当m=−54时，y=−−542−2×−54+3=6316，
∴点P的坐标为−54,6316；
答：PD+PE的最大值为498，点P的坐标为−54,6316；
（3）解：y=−x2−2x+3=−x+12+4，
则抛物线的顶点P−1，4，对称轴为x=−1，
情况一：当点N在y轴上时，P为抛物线的顶点，

∵四边形PMCN为矩形，
∴N与P纵坐标相同，
∴N0,4；
情况二：当点N在x轴负半轴上时，四边形PMCN为矩形，
过M作y轴的垂线，垂足为G，过P作x轴的垂线，垂足为H，

设Nt,0，则ON=−t，
∴∠MCN=∠CNP=90°，CM=NP，
∴∠MCG+∠OCN=90°，
∵∠ONC+∠OCN=90°，
∴∠MCG=∠ONC，
又∵∠CGM=∠CON=90°，
∴△CMG∽△NCO，
∴CGON=MGOC，
∵抛物线对称轴为x=−1，点M在对称轴上，C0,3，
∴MG=1，OC=3，
∴CG−t=13，即CG=−13t，
∵∠MCG+∠CMG=90°，∠ONC+∠PNH=90°，
∴∠CMG=∠PNH，
∴△CMG≌△PNH，
∴NH=MG=1，HP=CG=−13t，
∴OH=ON+NH=−t+1，
∴点P的坐标为t−1,−13t，
∵点P在抛物线上，
∴−13t=−t−12−2t−1+3，
解得t1=1−1456，t2=1+1456（舍去），
∴N1−1456,0，
综上所述：符合条件的N点坐标为：N0,4或N1−1456,0．
【点睛】本题考查二次函数的综合应用，涉及待定系数法，相似三角形的判定和性质，矩形的性质等知识，解题的关键是方程思想的应用．
类型三 菱形存在性问题
和平行四边形相比，菱形多一个“对角线互相垂直”或“邻边相等”，但这两者其实是等价的，故若四边形ABCD是菱形，则其4个点坐标需满足: xA+xC=xB+xDyA+yC=yB+yD（xA−xB）2+（yA−yB）2=（xC−xB）2+（yC−yB）2
解决问题的方法也可有如下两种:
思路 1:先平四，再菱形.设点坐标，根据平四存在性要求列出“4+C-B+D”(AC、BD 为对角线)，再结合组邻边相等，得到方程组，
思路 2:先等腰，再菱形.在构成菱形的4个点中任取3个点，必构成等三角形，根据等腰存在性方法可先确定第3个点，再确定第4个点.
1．（2023·西藏·中考真题）在平面直角坐标系中，抛物线y=−x2+bx+c与x轴交于A−3,0，B1,0两点，与y轴交于点C．

(1)求抛物线的解析式；
(2)如图甲，在y轴上找一点D，使△ACD为等腰三角形，请直接写出点D的坐标；
(3)如图乙，点P为抛物线对称轴上一点，是否存在P、Q两点使以点A，C，P，Q为顶点的四边形是菱形？若存在，求出P、Q两点的坐标，若不存在，请说明理由．
【答案】(1)y=−x2−2x+3；
(2)0，0或0，−3或0，3−32或0，3+32；
(3)存在，P−1，3−17，Q−4，−17或P−1，3+17，Q−4，17或P−1，1，Q−2，2或P−1，14，Q2，3+14或P−1,−14，Q2，3−14
【分析】（1）将A−3,0，B1,0代入y=−x2+bx+c，求出b,c,即可得出答案；
（2）分别以点D为顶点、以点A为顶点、当以点C为顶点，计算即可；
（3）抛物线y=−x2−2x+3的对称轴为直线x=−1，设P−1,t，Qm,n，求出AC2=18，AP2=t2+4，PC2=t2−6t+10，分三种情况：以AP为对角线或以AC为对角线或以CP为对角线．
【详解】（1）解：（1）∵A−3,0，B1,0两点在抛物线上，
∴0=−−32−3b+c0=−12+b+c
解得，b=−2c=3，
∴抛物线的解析式为：y=−x2−2x+3；
（2）令x=0，y=3，
∴C0，3，
由△ACD为等腰三角形，如图甲，

当以点D为顶点时，DA=DC，点D与原点O重合，
∴D0，0；
当以点A为顶点时，AC=AD，AO是等腰△ACD中线，
∴OC=OD，
∴D0，−3；
当以点C为顶点时，AC=CD=OA2+OC2=32+32=32
∴点D的纵坐标为3−32或32+3，
∴综上所述，点D的坐标为0，0或0，−3或0，3−32或0，3+32．
（3）存在，理由如下：
抛物线y=−x2−2x+3的对称轴为：直线x=−1，
设P−1,t，Qm,n，
∵A−3，0，C0，3，
则AC2=−32+32=18，
AP2=−1+32+t2=t2+4，
PC2=−12+t−32=t2−6t+10，
∵以A、C、P、Q为顶点的四边形是菱形，
∴分三种情况：以AP为对角线或以AC为对角线或以CP为对角线，
当以AP为对角线时，则CP=CA，如图1，

∴t2−6t+10=18，
解得：t=3±17，
∴P1−1，3−17或P2−1，3+17
∵四边形ACPQ是菱形，
∴AP与CQ互相垂直平分，即AP与CQ的中点重合，
当P1−1，3−17时，
∴m+02=−3−12，n+32=0+3−172，
解得：m=−4,n=−17，
∴Q1−4，−17
当P2−1，3+17时，
∴m+02=−3−12，n+32=0+3+172，
解得：m=−4,n=17，
∴Q2−4，17
以AC为对角线时，则PC=AP，如图2，

∴t2−6t+10=t2+4，
解得：t=1，
∴P3−1，1，
∵四边形APCQ是菱形，
∴AC与PQ互相垂直平分，即AC与CQ中点重合，
∴m−12=−3+02，n+12=0+32，
解得：m=−2,n=2，
∴Q3−2，2；
当以CP为对角线时，则AP=AC，如图3，

∴t2+4=18，
解得：t=±14，
∴P4−1,14,P5−1,−14，
∵四边形ACQP是菱形，
∴AQ与CP互相垂直平分，即AQ与CP的中点重合，
∴−3+m2=0−12,n+02=3±142，
解得：m=2,n=3±14
∴Q42,3+14,Q52,3−14，
综上所述，符合条件的点P、Q的坐标为： P−1，3−17，Q−4，−17或P−1，3+17，Q−4，17或P−1，1，Q−2，2或P−1，14，Q2，3+14或P−1,−14，Q2，3−14
【点睛】本题是二次函数综合题，考查了解析式的求法、等腰三角形的判定、菱形的性质、坐标与图形的性质、分类讨论等知识，熟练掌握菱形的性质和坐标与图形的性质是解题的关键．
2．（2023·四川广安·中考真题）如图，二次函数y=x2+bx+c的图象交x轴于点A，B，交y轴于点C，点B的坐标为1,0，对称轴是直线x=−1，点P是x轴上一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．

(1)求这个二次函数的解析式．
(2)若点P在线段AO上运动（点P与点A、点O不重合），求四边形ABCN面积的最大值，并求出此时点P的坐标．
(3)若点P在x轴上运动，则在y轴上是否存在点Q，使以M、N、C、Q为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．
【答案】(1)y=x2+2x−3
(2)S四边形ABCN最大值为758，此时P−32，0
(3)Q0，−1或Q0，32−1或Q0，−1−32
【分析】（1）先根据二次函数对称轴公式求出b=2，再把B1,0代入二次函数解析式中进行求解即可；
（2）先求出A−3，0，C0，−3，则AB=4，OC=3，求出直线AC的解析式为y=−x−3，设Pm，0，则Mm，−m−3，Nm，m2+2m−3，则MN=−m2−3m；再由S四边形ABCN=S△ABC+S△ACN得到S四边形ABCN=−32m+322+758，故当m=−32时，S四边形ABCN最大，最大值为758，此时点P的坐标为−32，0；
（3）分如图3-1，图3-2，图3-3，图3-4，图3-5，图3-6所示，MC为对角线和边，利用菱形的性质进行列式求解即可．
【详解】（1）解：∵二次函数y=x2+bx+c的对称轴为直线x=−1，
∴−b2=−1，
∴b=2，
∵二次函数经过点B1,0，
∴12+b+c=0，即1+2+c=0，
∴c=−3，
∴二次函数解析式为y=x2+2x−3；
（2）解：∵二次函数经过点B1,0，且对称轴为直线x=−1，
∴A−3，0，
∴AB=4，
∵二次函数y=x2+2x−3与y轴交于点C，
∴C0，−3，
∴OC=3；
设直线AC的解析式为y=kx+b'，
∴−3k+b'=0b'=−3，
∴k=−1b'=−3，
∴直线AC的解析式为y=−x−3，
设Pm，0，则Mm，−m−3，Nm，m2+2m−3，
∴MN=−m−3−m2+2m−3=−m2−3m；
∵S△ABC=12AB⋅OC=12×4×3=6，
∴S四边形ABCN=S△ABC+S△ACN
=S△ABC+S△AMN+S△CMN
=12AP⋅MN+12OP⋅MN+6
=12×3−m2−3m+6
=−32m+322+758，
∵−32<0，
∴当m=−32时，S四边形ABCN最大，最大值为758，
∴此时点P的坐标为−32，0；
（3）解：设Pm，0，则Mm，−m−3，Nm，m2+2m−3，
∵PM⊥x轴，
∴PM∥y轴，即MN∥CQ，
∴MN、CQ是以M、N、C、Q为顶点的菱形的边；
如图3-1所示，当MC为对角线时，

∵OA=OC=3，
∴△AOC是等腰直角三角形，
∴∠ACO=45°，
∵QM=QC，
∴∠QMC=∠QCM=45°，
∴∠MQC=90°，
∴MQ⊥y轴，
∴NC⊥y轴，即NC∥x轴，
∴点C与点N关于抛物线对称轴对称，
∴点N的坐标为−2，−3，
∴CQ=CN=2，
∴Q0，−1；
如图3-2所示，当MC为边时，则MN=CM，

∵Mm，−m−3，C0，−3，Nm，m2+2m−3
∴CM=m2+−m−3−−32=−2m，MN=m2+2m−3−−m−3=m2+3m
∴m2+3m=−2m，
解得m=−3−2或m=0（舍去），
∴CQ=CM=−2m=32+2，
∴Q0，32−1；
如图3-3所示，当MC为边时，则MN=CM，

同理可得CM=−2m，
∴−m2−3m=−2m，
解得m=2−3或m=0（舍去），
∴CQ=CM=−2m=32−2，
∴Q0，−1−32；
如图3-4所示，当MC为边时，则CM=MN，

同理可得m2+3m=2m，
解得m=2−3（舍去）或m=0（舍去）；
如图3-5所示，当MC为对角线时，

∴∠MCQ=∠ACO=45°，
∵CQ=MQ，
∴∠QCM=∠QMC=45°，
∴∠MQC=90°，
∴MQ⊥y轴，
∴NC⊥y轴，这与题意相矛盾，
∴此种情形不存在
如图3-6所示，当MC为对角线时，设MC，QN交于S，

∵MN∥y轴，
∴∠NMC=180°−∠MCO=135°，
∵NQ⊥CM，
∴∠NSM=90°，这与三角形内角和为180度矛盾，
∴此种情况不存在；
综上所述，Q0，−1或Q0，32−1或Q0，−1−32．
【点睛】本题主要考查了二次函数综合，一次函数与几何综合，菱形的性质，勾股定理，求二次函数解析式等等，利用分类讨论的思想求解是解题的关键．
类型四 正方形存在性问题
思路 1:从判定出发
1）若已知菱形，则加有一个角为直角或对角线相等:
2）若已知矩形，则加有一组邻边相等或对角线互相垂直:
3）若已知对角线互相垂直或平分或相等，则加上其他条件.
思路 2:构造三乖直全等
若条件并未给关于四边形及对角线的特殊性，则考虑在构成正方形的4个顶点中任取3个，必是等腰直角三角形，若已知两定点，则可通过构造三垂直全等来求得第3个点，再求第4点.
总结：构造三垂直全等的思路仅适合已知两定点的情形，若题目给了4个动点，则考虑矩形的判定出发，观察该四边形是否己为某特殊四边形，考证还需满足的其他关系.（正方形的存在性问题在中考中出现得并不多，正方形多以小题压轴为主）
1．（2023·辽宁·中考真题）如图，抛物线y=−12x2+bx+c与x轴交于点A和点B4，0，与y轴交于点C0，4，点E在抛物线上．

(1)求抛物线的解析式；
(2)点E在第一象限内，过点E作EF∥y轴，交BC于点F，作EH∥x轴，交抛物线于点H，点H在点E的左侧，以线段EF,EH为邻边作矩形EFGH，当矩形EFGH的周长为11时，求线段EH的长；
(3)点M在直线AC上，点N在平面内，当四边形OENM是正方形时，请直接写出点N的坐标．
【答案】(1)抛物线的解析式为y=−12x2+x+4；
(2)EH=4；
(3)点N的坐标为4，4或−72，32或−5+574,−17−3574或−5−574,−17+3574
【分析】（1）利用待定系数法即可求解；
（2）先求得直线BC的解析式为y=−x+4，设Ex，−12x2+x+4，则Fx，−x+4，利用对称性质求得H2−x，−12x2+x+4，推出GH=EF=−12x2+2x，GF=EH=2x−2，利用矩形周长公式列一元二次方程计算即可求解；
（3）先求得直线AC的解析式为y=2x+4，分别过点M、E作y的垂线，垂足分别为P、Q，证明△OEP≌△MOQ，推出PE=OQ，PO=MQ，设Em，−12m2+m+4，则M12m2−m−4，m，由点M在直线AC上，列式计算，可求得m的值，利用平移的性质可得点N的坐标；设点Ma,b，则点Eb,−a，当OM绕着点O逆时针旋转90°得到OE时，当点M绕点O逆时针90°得到点E时，根据旋转的性质，可得点N的坐标．
【详解】（1）解：∵抛物线y=−12x2+bx+c经过点B4，0和C0，4，
∴−12×42+4b+c=0c=4，
解得b=1c=4，
∴抛物线的解析式为y=−12x2+x+4；
（2）解：∵点B4，0和C0，4，
设直线BC的解析式为y=kx+4，则0=4k+4，
解得k=−1，
∴直线BC的解析式为y=−x+4，
设Ex，−12x2+x+4，且0∴GH=EF=−12x2+x+4−−x+4=−12x2+2x，
∵抛物线的对称轴为直线x=−12×−12=1，
∴H2−x，−12x2+x+4，
∴GF=EH=x−4−x=2x−2，
依题意得2−12x2+2x+2x−2=11，
解得x=5（舍去）或x=3，
∴EH=4；
（3）解：令y=0，则−12x2+x+4=0，
解得x=−2或x=4，
∴A−2，0，
同理，直线AC的解析式为y=2x+4，
∵四边形OENM是正方形，
∴OE=OM，∠EOM=90°，分别过点M、E作y的垂线，垂足分别为P、Q，如图，

∠OPE=∠MQO=90°，∠OEP=90°−∠EOP=∠MOQ，
∴△OEP≌△MOQ，
∴PE=OQ，PO=MQ，
设Em，−12m2+m+4，
∴PE=OQ=−m，PO=MQ=−12m2+m+4，
则M12m2−m−4，m，
∵点M在直线AC上，
∴m=212m2−m−4+4，
解得m=4或m=−1，
当m=4时，M0，4，E4，0，
即点M与点C重合，点E与点B重合时，四边形OENM是正方形，此时N4，4；
当m=−1时，M−52，−1，E−1，52，
点O向左平移52个单位，再向下平移1个单位，得到点M，
则点E向左平移52个单位，再向下平移1个单位，得到点N，
∴N−1−52，52−1，即N−72，32；
设点Ma,b，则点Eb,−a，
当OM绕着点O逆时针旋转90°得到OE时，如图，
∵点E在y=2x+4的图象上，
∴b=2a+4，
∴点Ma,2a+4，
∵点E在y=−12x2+x+4的图象上，
∴−122a+42+2a+4+4=−a，
解得：a=−52或0，
∴M10,4,E14,0,M2−52,−1，E2−1,52，
当点M绕点O逆时针90°得到点E时，点E−b,a，Ma,2a+4,E−2a−4,a，
∵点E在y=−12x2+x+4的图象上，
∴−12−2a−42−2a−4+4=a，
解得：a=−11±574，
∴点M1−11−574,−3−572，E13+572,−11−574，M2−11+574,−3+572，E23−572,−11+574，
∴点N的坐标为−5+574,−17−3574或−5−574,−17+3574；
综上，点N的坐标为4，4或−72，32或−5+574,−17−3574或−5−574,−17+3574．
【点睛】本题考查的是待定系数法求二次函数解析式，二次函数图象上点的坐标特征，待定系数法求一次函数解析式，一次函数图象上点的坐标特征，两点之间的距离公式和正方形的性质，是一道综合性较强的题，解题的关键是求出二次函数和一次函数解析式以及分情况讨论．
2．（2023·湖南岳阳·中考真题）已知抛物线Q1:y=−x2+bx+c与x轴交于A−3,0,B两点，交y轴于点C0,3．

(1)请求出抛物线Q1的表达式．
(2)如图1，在y轴上有一点D0,−1，点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E,F使得四边形DAEF为正方形？若存在，请求出点E,F的坐标；若不存在，请说明理由．
(3)如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK=∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】(1)y=−x2−2x+3
(2)E−2,3；F1,2
(3)点P的坐标为(1,0)或(−2,3)
【分析】
（1）把A−3，0，C0,3代入Q1:y=−x2+bx+c，求出b=−2,c=3即可；
（2）假设存在这样的正方形，过点E作ER⊥x于点R，过点F作FI⊥y轴于点I，证明△EAR≅△AOD,△FID≅△DOA，可得ER=3,AR=1,FI=1,IO=2,故可得E−2,3，F1,2；
（3）先求得抛物线Q2的解析式为y=−(x+1−2)2+4=−(x−1)2+4，得出K(1,4)，H(3,0)，运用待定系数法可得直线BC的解析式为y=−x+3，过点K作KT⊥y轴于点T，连接BC，设KP交直线BC于M或N，如图2，过点C作PS⊥y轴交BK于点S，交抛物线Q1于点P，连接PK，利用等腰直角三角形性质和三角函数定义可得tan∠CHK=CKCH=232=13，进而可求得点P的坐标．
【详解】（1）
∵抛物线Q1:y=−x2+bx+c与x轴交于A−3,0,两点，交y轴于点C0,3，
∴把A−3，0，C0,3代入Q1:y=−x2+bx+c，得，
−9−3b+c=0c=3,
解得，b=−2c=3,
∴解析式为：y=−x2−2x+3；
（2）假设存在这样的正方形DAEF，如图，过点E作ER⊥x于点R，过点F作FI⊥y轴于点I，

∴∠AER+∠EAR=90°,
∵四边形DAEF是正方形，
∴AE=AD,∠EAD=90°,
∴∠EAR+∠DAR=90°,
∴∠AER=∠DAO,
又∠ERA=∠AOD=90°,
∴△AER≅△DAO，
∴AR=DO,ER=AO,
∵A−3,0,D0,−1,
∴OA=3,OD=1,
∴AR=1,ER=3,
∴OR=OA−AR=3−1=2,
∴E−2,3；
同理可证明：△FID≅△DOA，
∴FI=DO=1,DI=AO=3,
∴IO=DI−DO=3−1=2,
∴F1,2；
（3）
解：抛物线Q1上存在点P，使得∠CPK=∠CHK．
∵y=−x2−2x+3=−(x+1)2+4，
∴抛物线Q1的顶点坐标为(−1,4)，
∵将抛物线Q1向右平移2个单位，得到抛物线Q2，
∴抛物线Q2的解析式为y=−(x+1−2)2+4=−(x−1)2+4，
∵抛物线Q2的顶点为K，与x轴正半轴交于点H，
∴K(1,4)，H(3,0)，
设直线BC的解析式为y=kx+n，把C(0,3)，H(3,0)代入得n=33k+n=0，
解得：k=−1n=3，
∴直线BC的解析式为y=−x+3，
过点K作KT⊥y轴于点T，连接BC，设KP交直线BC于M或N，如图2，过点C作PS⊥y轴交BK于点S，交抛物线Q1于点P，连接PK，
则T(0,4)，M(m,−m+3)，N(t,−t+3)，

∴KT=TC=1，∠KTC=90°，
∴△CKT是等腰直角三角形，
∴∠KCT=45°，CK=2KT=2，
∵OH=OC=3，∠COH=90°，
∴△COH是等腰直角三角形，
∴∠HCO=45°，CH=2OC=32，
∴∠KCH=180°−∠KCT−∠HCO=90°，
∴tan∠CHK=CKCH=232=13，
∵∠CPK=∠CHK，
∴tan∠CPK=tan∠CHK=13，
∵tan∠BCO=OBOC=13，
∴∠BCO=∠CHK，
∵BK∥OC，
∴∠CBK=∠BCO，
∴∠CBK=∠CHK，
即点P与点B重合时，∠CPK=∠CHK，
∴P1(1,0)；
∵SK=1，PS=3，
∴tan∠CPK=SKPS=13，
∴∠CPK=∠CHK，
∵点P与点C关于直线x=−1对称，
∴P(−2,3)；
综上所述，抛物线Q1上存在点P，使得∠CPK=∠CHK，点P的坐标为(1,0)或(−2,3)．
【点睛】本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，正方形的性质等知识，运用数形结合思想解决问题是解题的关键．
类型五 等腰三角形存在性问题
问题总结:
1) 两定一动:动点可在直线上、抛物线上;
2）一定两动:两动点必有关联，可表示线段长度列方程求解;
3）三动点:分析可能存在的特殊边、角，以此为突破口.
1．（2023·青海·中考真题）如图，二次函数y=−x2+bx+c的图象与x轴相交于点A和点C1,0，交y轴于点B0,3．

(1)求此二次函数的解析式；
(2)设二次函数图象的顶点为P，对称轴与x轴交于点Q，求四边形AOBP的面积（请在图1中探索）；
(3)二次函数图象的对称轴上是否存在点M，使得△AMB是以AB为底边的等腰三角形？若存在，请求出满足条件的点M的坐标；若不存在，请说明理由（请在图2中探索）．
【答案】(1)y=−x2−2x+3；
(2)152；
(3)M(−1，1)
【分析】（1）将B，C两点坐标代入抛物线的解析式，进一步求解得出结果；
（2）连接OP，将二次函数的解析式配方求得顶点的坐标，邻y=0求得A的坐标，从而求得OQ，PQ，OA的长，再根据S四边形AOBP=S△AOP+S△BOP求得结果；
（3）设M(−1，m)，表示出AM和BM，根据AM2=BM2列出方程求得m的值，进而求得结果．
【详解】（1）解：由题意得，
−1+b+c=0c=3，
∴b=−2c=3，
∴y=−x2−2x+3；
（2）解：如图，连接OP，

∵y=−x2−2x+3=−x+12+4，
∴P(−1，4)，
∴PQ=4，OQ=1，
由−x2−2x+3=0得，x1=1，x2=−3，
∴OA=3，
∴S四边形AOBP=S△AOP+S△BOP=12OA⋅PQ+12OB⋅OQ=12×3×4+12×3×1=152；
（3）解：设M(−1，m)，
∵OA=3，
∴A−3，0，
由AM2=BM2得−3−−12+m2=−12+m−32，
∴m=l，
∴M(−1，1)．
【点睛】本题考查了二次函数及其图象的性质，等腰三角形的判定，勾股定理等知识，解决问题的关键是熟练掌握有关基础知识．
2．（2022·贵州黔东南·中考真题）如图，抛物线y=ax2+2x+c的对称轴是直线x=1，与x轴交于点A，B3,0，与y轴交于点C，连接AC．
(1)求此抛物线的解析式；
(2)已知点D是第一象限内抛物线上的一个动点，过点D作DM⊥x轴，垂足为点M，DM交直线BC于点N，是否存在这样的点N，使得以A，C，N为顶点的三角形是等腰三角形．若存在，请求出点N的坐标，若不存在，请说明理由；
(3)已知点E是抛物线对称轴上的点，在坐标平面内是否存在点F，使以点B、C、E、F为顶点的四边形为矩形，若存在，请直接写出点F的坐标；若不存在，请说明理由．
【答案】(1)y=−x2+2x+3
(2)存在这样的点N（2，1）或5,−5+3或52,12，使得以A，C，N为顶点的三角形是等腰三角形
(3)存在点F的坐标为（4，1）或（-2，1）或2,3+172或2,3−172．
【分析】（1）根据抛物线的对称轴是直线x=1，可得a=-1，再把点B3,0代入，即可求解；
（2）先求出AC2=OA2+OC2=10，设点N（m，-m+3），可得AN2=2m2−4m+10，CN2=2m2，再分三种情况讨论：当AC=AN时，当AC=CN时，当AN=CN时，即可求解；
（3）设点E（1，n），点F（s，t），然后分两种情况讨论：当BC为边时，当BC为对角线时，即可求解．
【详解】（1）解：∵抛物线y=ax2+2x+c的对称轴是直线x=1，
∴−22a=1，解得：a=-1，
∵抛物线过点B3,0，
∴−9+6+c=0，解得：c=3，
∴抛物线解析式为y=−x2+2x+3；
（2）解：存在这样的点N，使得以A，C，N为顶点的三角形是等腰三角形．理由如下：
令y=0，则−x2+2x+3=0，
解得：x1=3,x2=−1，
∴点A的坐标为（-1，0），
∴OA=1，
当x=0时，y=3，
∴点C的坐标为（0，3），即OC=3，
∴AC2=OA2+OC2=10，
设直线BC的解析式为y=kx+bk≠0，
把点B（3，0），C（0，3）代入得：
3k+b=0b=3，解得：k=−1b=3，
∴直线BC的解析式为y=−x+3，
设点N（m，-m+3），
∴MN=-m+3，AM=m+1，
∴AN2=−m+32+m+12=2m2−4m+10，CN2=m2+−m+3−32=2m2，
当AC=AN时，2m2−4m+10=10，
解得：m=2或0（舍去），
∴此时点N（2，1）；
当AC=CN时，2m2=10，
解得：m=5或−5（舍去），
∴此时点N5,−5+3；
当AN=CN时，2m2=2m2−4m+10，
解得：m=52，
∴此时点N52,12；
综上所述，存在这样的点N（2，1）或5,−5+3或52,12，使得以A，C，N为顶点的三角形是等腰三角形；
（3）解：存在，理由如下：
∵点B（3，0），C（0，3），
∴OB=OC，
∴BC=32，
设点E（1，n），点F（s，t），
当BC为边时，点C向右平移3个单位向下平移3个单位得到点B，同样E（F）向右平移3个单位向下平移3个单位得到点F（E），且BE=CF（CE=BF），如图，
∴1+3=sn−3=t1−32+n2=s2+t−32或s+3=1t−3=n1−02+n−32=(s−3)2+t−02，
解得：n=4s=4t=1或n=−2s=−2t=1，
∴此时点F的坐标为（4，1）或（-2，1）；
当BC为对角线时，BC=EF，且EF与BC的中点重合，如图，
1+s2=32n+t2=321−s2+n−t2=32，解得：n=3+172s=2t=3−172或n=3−172s=2t=3+172，
∴此时点F的坐标为2,3+172或2,3−172；
综上所述，存在点F的坐标为（4，1）或（-2，1）或2,3+172或2,3−172．
【点睛】本题主要考查了二次函数的综合题，熟练掌握二次函数的图象和性质，等腰三角形的性质，矩形的性质，并利用分类讨论思想解答是解题的关键是解题的关键．
3．（2022·山西·中考真题）综合与探究
如图，二次函数y=−14x2+32x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m．过点P作直线PD⊥x轴于点D，作直线BC交PD于点E
(1)求A，B，C三点的坐标，并直接写出直线BC的函数表达式；
(2)当△CEP是以PE为底边的等腰三角形时，求点P的坐标；
(3)连接AC，过点P作直线l∥AC ，交y轴于点F，连接DF．试探究：在点P运动的过程中，是否存在点P，使得CE=FD，若存在，请直接写出m的值；若不存在，请说明理由．
【答案】(1)A−2,0,B8,0，点C的坐标为0,4；y=−12x+4
(2)4,6
(3)存在；m的值为4或25−2
【分析】（1）令y=−14x2+32x+4中y和x分别为0，即可求出A，B，C三点的坐标，利用待定系数法求直线BC的函数表达式；
（2）过点C作CG⊥PD于点G，易证四边形CODG是矩形，推出CG∥OB，DG=OC=4，CG=OD=m，再证明△CGE∽△BOC，推出EG=12m，由等腰三角形三线合一的性质可以得出PG=EG=12m， 则PD=PG+DG=12m+4，由P点在抛物线上可得PD=−14m2+32m+4，联立解出m，代入二次函数解析式即可求出点P的坐标；
（3）分点F在y轴的负半轴上和点F在y轴的正半轴上两种情况，画出大致图形，当CE=FD时，EG=OF，由（2）知EG=12m，用含m的代数式分别表示出OF，列等式计算即可．
【详解】（1）解：由y=−14x2+32x+4得，
当x=0时，y=4，
∴点C的坐标为0,4．
当y=0时，−14x2+32x+4=0，
解得x1=−2,x2=8．
∵点A在点B的左侧，
∴点A，B的坐标分别为A−2,0,B8,0．
设直线BC的函数表达式为y=kx+b，
将B8,0，C0,4代入得0=8k+b4=b，
解得k=−12b=4，
∴直线BC的函数表达式为y=−12x+4﹒
（2）解：∵点P在第一象限抛物线上，横坐标为m，且PD⊥x轴于点D，
∴点P的坐标为m,−14m2+32m+4，OD=m，
∴PD=−14m2+32m+4．
∵点B的坐标为8,0，点C的坐标为0,4，
∴OB=8，OC=4．
过点C作CG⊥PD于点G，则∠CGD=90°．
∵∠PDO=∠COD=90°，
∴四边形CODG是矩形，
∴CG∥OB ，DG=OC=4，CG=OD=m．
∴∠1=∠2．
∵∠CGE=∠BOC=90°，
∴△CGE∽△BOC．
∴EGCO=CGBO，即EG4=m8，
∴EG=12m．
在△CPE中，
∵CP=CE,CG⊥PE，
∴PG=EG=12m．
∴PD=PG+DG=12m+4，
∴−14m2+32m+4=12m+4
解得m1=4,m2=0（舍去），
∴m=4．
当m=4时，y=−14m2+32m+4=6﹒
∴点P的坐标为4,6．
（3）解：存在；m的值为4或25−2．
分两种情况，①当点F在y轴的负半轴上时，如下图所示，过点P作直线PH⊥y轴于点H，
∵过点P作直线l∥AC，交y轴于点F，
∴PF∥AC ，
∴∠ACO=∠PFH，
∴tan∠ACO=tan∠PFH，
∴AOOC=HPHF，即24=mHF，
∴HF=2m，
∵OH=PD=−14m2+32m+4，
∴OF=HF−OH=2m−−14m2+32m+4=14m2+12m−4，
由（2）知，EG=12m．
根据勾股定理，在△CGE中，CE2=CG2+GE2，
在△FOD中，FD2=OF2+OD2，
当CE=FD时，CG2+GE2=OF2+OD2，
∵CG=OD=m，
∴EG=OF，
∴12m=14m2+12m−4，
解得m=4或m=−4，
∵点P是第一象限内二次函数图象上的一个动点，
∴m=4；
②当点F在y轴的正半轴上时，如下图所示，
同理可得，EG=OF，EG=12m，HF=2m，OH=PD=−14m2+32m+4，
∴OF=OH−HF=−14m2+32m+4−2m=−14m2−12m+4
∴12m=−14m2−12m+4，
解得m=25−2或m=−25−2，
∵点P是第一象限内二次函数图象上的一个动点，
∴m=25−2；
综上，m的值为4或25−2
【点睛】本题属于二次函数综合题，考查了二次函数、一次函数、等腰三角形、矩形、勾股定理、相似三角形等知识点，第三问难度较大，需要分情况讨论，画出大致图形，用含m的代数式表示出OF是解题的关键．
类型六 直角三角形存在性问题
1．（2022·四川广安·中考真题）如图，在平面直角坐标系中，抛物线y=ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，－4），点C坐标为（2，0）．
(1)求此抛物线的函数解析式．
(2)点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．
(3)点P为该抛物线对称轴上的动点，使得△PAB为直角三角形，请求出点P的坐标．
【答案】(1)y=12x2+x−4
(2)（-2，-4）
(3)P点坐标为：（-1，3），（-1，-5），−1，−2+7，−1，−2−7
【分析】（1）直接将B（0，-4），C（2，0）代入y=ax2+x+m，即可求出解析式；
（2）先求出直线AB关系式为：y=−x−4，直线AB平移后的关系式为：y=−x−4+n，当其与抛物线只有一个交点时，此时点D距AB最大，此时△ABD的面积最大，由此即可求得D点坐标；
（3）分三种情况讨论，①当∠PAB=90°时，即PA⊥AB，则设PA所在直线解析式为：y=x+z，将A（-4,0）代入y=x+z得，解得：z=4，此时P点坐标为：（-1,3）；②当∠PBA=90°时，即PB⊥AB，则设PB所在直线解析式为：y=x+t，将B（0，-4）代入y=x+t得，t=−4，此时P点坐标为：（-1,-5）；③当∠APB=90°时，设P点坐标为：−1，yp，由于PA所在直线斜率为：yp3，PB在直线斜率为：yp+4−1，yp3· yp+4−1=-1，则此时P点坐标为：−1，−2+7，−1，−2−7．
【详解】（1）解：将B（0，-4），C（2，0）代入y=ax2+x+m，
得：m=−44a+2+m=0，
解得：m=−4a=12，
∴抛物线的函数解析式为：y=12x2+x−4．
（2）向下平移直线AB，使平移后的直线与抛物线只有唯一公共点D时，此时点D到直线AB的距离最大，此时△ABD的面积最大，
∵12x2+x−4=0时，x1=2，x2=−4，
∴A点坐标为：（-4,0），
设直线AB关系式为：y=kx+b（k≠0），
将A（-4,0），B（0，-4），代入y=kx+b（k≠0），
得：−4k+b=0b=−4，
解得：k=−1b=−4，
∴直线AB关系式为：y=−x−4，
设直线AB平移后的关系式为：y=−x−4+n，
则方程−x−4+n=12x2+x−4有两个相等的实数根，
即12x2+2x−n=0有两个相等的实数根，
∴n=−2，
即12x2+2x+2=0的解为：x=-2，
将x=-2代入抛物线解析式得，y=12×−22−2−4=−4，
∴点D的坐标为：（-2，-4）时，△ABD的面积最大；
（3）①当∠PAB=90°时，
即PA⊥AB，则设PA所在直线解析式为：y=x+z，
将A（-4,0）代入y=x+z得，−4+z=0，
解得：z=4，
∴PA所在直线解析式为：y=x+4，
∵抛物线对称轴为：x=-1，
∴当x=-1时，y=−1+4=3，
∴P点坐标为：（-1，3）；
②当∠PBA=90°时，
即PB⊥AB，则设PB所在直线解析式为：y=x+t，
将B（0，-4）代入y=x+t得，t=−4，
∴PA所在直线解析式为：y=x−4，
∴当x=-1时，y=−1−4=−5，
∴P点坐标为：（-1，-5）；
③当∠APB=90°时，设P点坐标为：−1，yp，
∴PA所在直线斜率为：yp3，PB在直线斜率为：yp+4−1，
∵PA⊥PB，
∴yp3· yp+4−1=-1，
解得：yp1=−2+7，yp2=−2−7，
∴P点坐标为：−1，−2+7，−1，−2−7
综上所述，P点坐标为：（-1，3），（-1，-5），−1，−2+7，−1，−2−7时，△PAB为直角三角形．
【点睛】本题主要考查的是二次函数图象与一次函数、三角形的综合，灵活运用所学知识是解题的关键．
2．（2023·江苏·中考真题）如图，二次函数y=12x2+bx−4的图像与x轴相交于点A(−2,0)、B，其顶点是C．

(1)b=_______；
(2)D是第三象限抛物线上的一点，连接OD，tan∠AOD=52；将原抛物线向左平移，使得平移后的抛物线经过点D，过点(k,0)作x轴的垂线l．已知在l的左侧，平移前后的两条抛物线都下降，求k的取值范围；
(3)将原抛物线平移，平移后的抛物线与原抛物线的对称轴相交于点Q，且其顶点P落在原抛物线上，连接PC、QC、PQ．已知△PCQ是直角三角形，求点P的坐标．
【答案】(1)−1；
(2)k≤−3；
(3)3,−52或−1,−52．
【分析】
（1）把A(−2,0)代入y=12x2+bx−4即可求解；
（2）过点D作DM⊥OA于点M，设Dm,12m2−m−4，由tan∠AOD=DMOM=−12m2+m+4−m=52，解得D−1,−52，进而求得平移后得抛物线，
平移后得抛物线为y=12x+32−92，根据二次函数得性质即可得解；
（3）先设出平移后顶点为Pp,12p2−p−4，根据原抛物线y=12x−12−92，求得原抛物线的顶点C1,−92，对称轴为x=1，进而得Q1,p2−2p−72，再根据勾股定理构造方程即可得解．
【详解】（1）
解：把A(−2,0)代入y=12x2+bx−4得，
0=12×−22+b×−2−4，
解得b=−1，
故答案为−1；
（2）
解：过点D作DM⊥OA于点M，

∵b=−1，
∴二次函数的解析式为y=12x2−x−4
设Dm,12m2−m−4，
∵D是第三象限抛物线上的一点，连接OD，tan∠AOD=52，
∴tan∠AOD=DMOM=−12m2+m+4−m=52，
解得m=−1或m=8（舍去），
当m=−1时，12m2−m−4=12+1−4=−52，
∴D−1,−52，
∵y=12x2−x−4=12x−12−92，
∴设将原抛物线向左平移后的抛物线为y=12x+a2−92，
把D−1,−52代入y=12x+a2−92得−52=12−1+a2−92，
解得a=3或a=−1（舍去），
∴平移后得抛物线为y=12x+32−92
∵过点(k,0)作x轴的垂线l．已知在l的左侧，平移前后的两条抛物线都下降，
在y=12x+32−92的对称轴x=−3的左侧，y随x的增大而减小，此时原抛物线也是y随x的增大而减小，
∴k≤−3；
（3）
解：由y=12x−12−92，设平移后的抛物线为y=12x−p2+q，则顶点为Pp,q，
∵顶点为Pp,q在y=12x−12−92上，
∴q=12p−12−92=12p2−p−4，
∴平移后的抛物线为y=12x−p2+12p2−p−4，顶点为Pp,12p2−p−4，
∵原抛物线y=12x−12−92，
∴原抛物线的顶点C1,−92，对称轴为x=1，
∵平移后的抛物线与原抛物线的对称轴相交于点Q，
∴Q1,p2−2p−72，
∵点Q、C在直线x=1上，平移后的抛物线顶点P在原抛物线顶点C的上方，两抛物线的交点Q在顶点P的上方，
∴∠PCQ与∠CQP都是锐角，
∵△PCQ是直角三角形，
∴∠CPQ=90°，
∴QC2=PC2+PQ2，
∴p2−2p−72+922=p−12+12p2−p−4+922+p−12+12p2−p−4−p2+2p+722化简得p−12p−3p+1=0，
∴p=1（舍去），或p=3或p=−1，
当p=3时，12p2−p−4=12×32−3−4=−52，
当p=−1时，12×−12+1−4=−52，
∴点P坐标为3,−52或−1,−52．
【点睛】本题考查了二次函数的图像及性质，勾股定理，解直角三角形以及待定系数法求二次函数的解析式，熟练掌握二次函数的图像及性质是解题的关键．
3．（2023·四川内江·中考真题）如图，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于B4,0，C−2,0两点．与y轴交于点A0,−2．

(1)求该抛物线的函数表达式；
(2)若点P是直线AB下方抛物线上的一动点，过点P作x轴的平行线交AB于点K，过点P作y轴的平行线交x轴于点D，求与12PK+PD的最大值及此时点P的坐标；
(3)在抛物线的对称轴上是否存在一点M，使得△MAB是以AB为一条直角边的直角三角形：若存在，请求出点M的坐标，若不存在，请说明理由．
【答案】(1)y=14x2−12x−2
(2)存在，12PK+PD的最大值为258，P32,−3516
(3)1,6或1,−4
【分析】（1）将A、B、C代入抛物线解析式求解即可；
（2）可求直线AB的解析式为y=12x−2，设Pm,14m2−12m−2（0（3）过A作AM2⊥AB交抛物线的对称轴于M2，过B作BM1⊥AB交抛物线的对称轴于M1，连接AM1，设M11,n， 可求AM12=n2+4n+5，BM12=n2+9，由AB2+BM12=AM12，可求M1，进而求出直线BM1的解析式，即可求解．
【详解】（1）解：由题意得
16a+4b+c=04a−2b+c=0c=−2，
解得：a=14b=−12c=−2，
∴抛物线的解析式为y=14x2−12x−2．
（2）解：设直线AB的解析式为y=kx+b，则有
4k+b=0b=−2，
解得：k=12b=−2，
∴直线AB的解析式为y=12x−2；
设Pm,14m2−12m−2（0∴12x−2=14m2−12m−2，
解得：x=12m2−m，
∴K12m2−m,14m2−12m−2，
∴PK=m−12m2−m
=−12m2+2m，
∴12PK=−14m2+m，
PD=−14m2−12m−2
=−14m2+12m+2，
∴12PK+PD=−14m2+m−14m2+12m+2
=−12m2+32m+2
=−12m−322+258，
∵−12<0，
∴当m=32时，12PK+PD的最大值为258，
∴ y=14×322−12×32−2=−3516，
∴ P32,−3516．
故12PK+PD的最大值为258，P32,−3516．
（3）解：存在，
如图，过A作AM2⊥AB交抛物线的对称轴于M2，过B作BM1⊥AB交抛物线的对称轴于M1，连接AM1，

∵抛物线y=14x2−12x−2的对称轴为直线x=1，
∴设M11,n，
∴AM12=12+n+22
=n2+4n+5，
AB2=22+42=20，
BM12=4−12+n2
=n2+9，
∵AB2+BM12=AM12，
∴n2+9+20=n2+4n+5，
解得：n=6，
∴M11,6；
设直线BM1的解析式为y=k1x+b1，则有
k1+b1=64k1+b1=0，
解得k1=−2b1=8，
∴直线BM1解析式为y=−2x+8，
∵AM2∥BM1，且经过A0,−2，
∴直线AM2解析式为y=−2x−2，
∴当x=1时，y=−2×1−2=−4，
∴M21,−4；
综上所述：存在，M的坐标为1,6或1,−4．
【点睛】本题考查了待定系数法求函数解析式，二次函数中动点最值问题，直角三角形的判定，勾股定理等，掌握解法及找出动点坐标满足的函数解析式是解题的关键．
类型七 相似三角形存在性问题
【相似判定】
判定1:三边对应成比例的两个三角形是相似三角形；
判定2:两边对应成比例且夹角相等的两个三角形是相似三角形；
判定3:有两组角对应相等的三角形是相似三角形.
【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等.所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角.然后再找：1）两相等角的两边对应成比例；2)还存在另一组角相等.事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1.
【解题方法】1)找对应等角2)分类讨论3)设点表示线段4)列方程求解5)检验
1．（2023·湖北随州·中考真题）如图1，平面直角坐标系xOy中，抛物线y=ax2+bx+c过点A(−1,0)，B(2,0)和C(0,2)，连接BC，点P(m,n) (m>0)为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M，交x轴于点N．

(1)直接写出抛物线和直线BC的解析式；
(2)如图2，连接OM，当△OCM为等腰三角形时，求m的值；
(3)当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似（其中点P与点C相对应），若存在，直接写出点P和点Q的坐标；若不存在，请说明理由．
【答案】(1)抛物线：y=−x2+x+2；直线BC：y=−x+2
(2)m=1或m=2或m=2
(3)P(2,2)，Q(0,2−1)或P(1+3,−1−3)，Q(0,1)或P(1+5,−3−5)，Q(0,−2)
【分析】
（1）由题得抛物线的解析式为y=a(x+1)(x−2)，将点C(0,2)代入求a，进而得抛物线的解析式；设直线BC的解析式为y=kx+t，将点B，C的坐标代入求k，t，进而得直线BC的解析式．
（2）由题得M(m,−m+2)，分别求出OC，OM，CM，对等腰△OCM中相等的边进行分类讨论，进而列方程求解；
（3）对点P在点B左侧或右侧进行分类讨论，设法表示出各线段的长度，利用相似三角形的相似比求解m，进而可得P，Q的坐标．
【详解】（1）解：∵抛物线过点A(−1,0)，B(2,0)，
∴抛物线的表达式为y=a(x+1)(x−2)，
将点C(0,2)代入上式，得2=−2a，
∴ a=−1．
∴抛物线的表达式为y=−(x+1)(x−2)，即y=−x2+x+2．
设直线BC的表达式为y=kx+t，
将点B(2,0)，C(0,2)代入上式，
得0=2k+t2=t，
解得k=−1t=2．
∴直线BC的表达式为y=−x+2．
（2）解：∵点M在直线BC上，且P(m,n)，
∴点M的坐标为(m,−m+2)．
∴ OC=2，CM2=(m−0)2+(−m+2−2)2=2m2，OM2=m2+(−m+2)2=2m2−4m+4．
当△OCM为等腰三角形时，
①若CM=OM，则CM2=OM2，
即2m2=2m2−4m+4，
解得m=1．
②若CM=OC，则CM2=OC2，
即2m2=4，
解得m=2或m=−2（舍去）．
③若OM=OC，则OM2=OC2，
即2m2−4m+4=4，
解得m=0（舍去）或m=2．
综上，m=1或m=2或m=2．
（3）解：∵点P与点C相对应，
∴ △POQ∽△CBN或△POQ∽△CNB．
①若点P在点B左侧，
则∠CBN=45°，BN=2−m，CB=22．
当△POQ∽△CBN，即∠POQ=45°时，
直线OP的表达式为y=x，
∴ −m2+m+2=m，解得m=2或m=−2（舍去）．
∴ OP2=(2)2+(2)2=4，即OP=2．
∴ OPBC=OQBN，即222=OQ2−2，
解得OQ=2−1．
∴ P(2,2)，Q(0,2−1)．
当△POQ∽△CNB，即∠PQO=45°时，
PQ=2m，OQ=−m2+m+2+m=−m2+2m+2，
∴ PQCB=OQNB，即2m22=−m2+2m+22−m，
解得m=1+5（舍去）或m=1−5（舍去）．
②若点P在点B右侧，
则∠CBN=135°，BN=m−2．
当△POQ∽△CBN，即∠POQ=135°时，
直线OP的表达式为y=−x，
∴ −m2+m+2=−m，解得m=1+3或m=1−3（舍去），
∴ OP=2m=2+6，
∴ OPBC=OQBN，即2+622=OQ3−1，
解得OQ=1．
∴ P(1+3,−1−3)，Q(0,1)．
当△POQ∽△CNB，即∠PQO=135°时，
PQ=2m，OQ=−m2+m+2+m=m2−2m−2．
∴ PQCB=OQNB，即2m22=m2−2m−2m−2，
解得m=1+5或m=1−5（舍去）．
∴ P(1+5,−3−5)，Q(0,−2)．
综上，P(2,2)，Q(0,2−1)或P(1+3,−1−3)，Q(0,1)或P(1+5,−3−5)，Q(0,−2)．
【点睛】本题是二次函数的综合应用，考查了待定系数法求函数解析式，等腰三角形的性质与判定，平面直角坐标系中两点距离的算法，相似三角形的性质与判定等，熟练掌握相关知识是解题的关键．
2．（2022·湖北恩施·中考真题）在平面直角坐标系中，O为坐标原点，抛物线y=−x2+c与y轴交于点P0,4．
(1)直接写出抛物线的解析式．
(2)如图，将抛物线y=−x2+c向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．
(3)直线BC与抛物线y=−x2+c交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．
(4)若将抛物线y=−x2+c进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出拋物线y=−x2+c平移的最短距离并求出此时抛物线的顶点坐标．
【答案】(1)y=−x2+4
(2)以B、C、Q三点为顶点的三角形是直角三角形，理由见解析
(3)存在，T25+13,0或T3+54,0，
(4)最短距离为528，平移后的顶点坐标为58,278
【分析】（1）待定系数法求二次函数解析式；
（2）分别求得B、C、Q的坐标，勾股定理的逆定理验证即可求解；
（3）由∠CBA=∠NBT，故分两种情况讨论，根据相似三角形的性质与判定即可求解；
（4）如图，作l∥BC且与抛物线只有1个交点，交y轴于点D，过点C作CE⊥l于点E，则△DEC是等腰直角三角形，作EF⊥DC于F，进而求得直线l与BC的距离，即为所求最短距离，进而求得平移方式，将顶点坐标平移即可求解．
【详解】（1）解：∵抛物线y=−x2+c与y轴交于点P0,4
∴c=4
∴抛物线解析式为y=−x2+4
（2）以B、C、Q三点为顶点的三角形是直角三角形，理由如下：
∵ y=−x2+4的顶点坐标为P0,4
依题意得，Q−1,4
∴平移后的抛物线解析式为y=−x+12+4
令y=0，解−x+12+4=0
得x1=−3,x2=1
∴A1,0，B−3,0
令x=0，则y=3，即C0,3
∴BC2=32+32=18，CQ2=12+12=2，QB2=−3+12+42=20
∴BC2+CQ2=QB2
∴以B、C、Q三点为顶点的三角形是直角三角形
（3）存在，T25+13,0或T3+54,0，理由如下，
∵B−3,0，C0，3，
∴OB=OC=3
∴ △OBC是等腰直角三角形
设直线BC的解析式为y=kx+b，
则−3k+b=0b=3，
解得k=1b=3，
∴直线BC的解析式为y=x+3，
联立y=x+3y=−x2+4
解得x1=−1+52y1=5+52，x2=−1−52y2=5−52
∴N−1+52,5+52
∵ A1,0,B−3,0，C0,3，△OBC是等腰直角三角形
∴ AB=4，BC=2OB=32
设直线AC的解析式为y=mx+n,
∴m+n=0n=3
∴m=−3n=3
∴直线AC的解析式为y=−3x+3
当NT∥AC时，△BNT∽△BCA
设NT的解析式为y=−3x+t，由NT过点N−1+52,5+52
则5+52=−3−1+52+t
解得t=25+1
∴ NT的解析式为y=−3x+25+1，
令y=0
解得x=25+13
∴T25+13,0
∴BT=3+25+13=10+253
∵ △BNT∽△BCA，
∴BTBA=BNBC
∴10+2534=BN32
∴BN=522+102
②当△BNT∽△BAC时，则BTBC=BNBA
即BT32=522+1024
解得BT=154+354
∵OB=3
∴T3+54,0
综上所述，T25+13,0或T3+54,0
（4）如图，作l∥BC，交y轴于点D，过点C作CE⊥l于点E，则△DEC是等腰直角三角形，作EF⊥DC于F
∵直线BC的解析式为y=x+3
设与BC平行的且与y=−x2+4只有一个公共点的直线l解析式为y=x+b
则y=−x2+4y=x+b
整理得：x2+x+b−4=0
则Δ=12−4b−4=0
解得b=174
∴直线l的解析式为y=x+174
∴CD=174−3=54，EF=FC=12CD=58
∴CE=22CD=22×54=528
即拋物线y=−x2+c平移的最短距离为528，方向为EC方向
∵P0,4
∴把点P先向右平移EF的长度，再向下平移FC的长度即得到平移后的坐标
∴平移后的顶点坐标为58,4−58，即58，278
【点睛】本题是二次函数综合，考查了相似三角形的性质，求二次函数与一次函数解析式，二次函数图象的平移，勾股定理的逆定理，正确的添加辅助线以及正确的计算是解题的关键．
3．（2022·湖南衡阳·中考真题）如图，已知抛物线y=x2−x−2交x轴于A、B两点，将该抛物线位于x轴下方的部分沿x轴翻折，其余部分不变，得到的新图象记为“图象W”，图象W交y轴于点C．
(1)写出图象W位于线段AB上方部分对应的函数关系式；
(2)若直线y=−x+b与图象W有三个交点，请结合图象，直接写出b的值；
(3)P为x轴正半轴上一动点，过点P作PM∥y轴交直线BC于点M，交图象W于点N，是否存在这样的点P，使△CMN与△OBC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
【答案】(1)y=−x2+x+2−1(2)b=2或b=3
(3)存在，1,0或1+172,0或1+5,0
【分析】（1）先求出点A、B、C坐标，再利用待定系数法求解函数关系式即可；
（2）联立方程组，由判别式△=0求得b值，结合图象即可求解；
（3）根据相似三角形的性质分∠CNM=90°和∠NCM=90°讨论求解即可．
【详解】（1）解：由翻折可知：C0,2.
令x2−x−2=0，解得：x1=−1，x2=2，
∴A−1,0，B2,0，
设图象W的解析式为y=ax+1x−2，代入C0,2，解得a=−1，
∴对应函数关系式为y=−x+1x−2=−x2+x+2 −1（2）解：联立方程组y=−x+by=−x2+x+2，
整理，得：x2−2x+b−2=0，
由△=4-4（b-2）=0得：b=3，此时方程有两个相等的实数根，
由图象可知，当b=2或b=3时，直线y=−x+b与图象W有三个交点；
（3）解：存在．如图1，当CN∥OB时，△OBC∽△NMC，此时，N与C关于直线x= 12 对称，
∴点N的横坐标为1，∴P1,0；
如图2，当CN∥OB时，△OBC∽△NMC，此时，N点纵坐标为2，
由x2−x−2=2，解得x1=1+172，x2=1−172（舍），
∴N的横坐标为1+172，
所以P1+172,0；
如图3，当∠NCM=90°时，△OBC∽△CMN，此时，直线CN的解析式为y=x+2，
联立方程组：y=x+2y=x2−x−2，解得x1=1+5，x2=1−5（舍），
∴N的横坐标为1+5，
所以P1+5,0，
因此，综上所述：P点坐标为1,0或1+172,0或1+5,0．
【点睛】本题考查二次函数的综合，涉及翻折性质、待定系数法求二次函数解析式、二次函数与一次函数的图象交点问题、相似三角形的性质、解一元二次方程等知识，综合体现数形结合思想和分类讨论思想的运用，属于综合题型，有点难度．
类型八 等角存在性问题
【常见的构角方法】
1）平行线的同位角、内错角相等；
2）等腰三角形的等边对等角；
3）角平分线分的两个角相等；
4）全等（相似）三角形对应角相等；
5）若两角的三角函数值相等，则两角相等；
6）同圆或等圆中，同弧或等弧所对的圆周角相等.
探究角度问题的一般步骤如下：
1）读题、理解题意，画图；
2）分析动点、定点、找不变特征（如角有两边，其中一条边是确定的）；
3）确定分类特征，进行分类讨论；
4）将角度进行转化.
角度转化的一般方法为：
通过锐角三角形函数、特殊角的三角函数值，相似三角形或等腰三角形的性质，转化为常见的类型，然后利用解直角三角形、相似三角形边的比例关系作为计算工具去计算求解，难度相对较大.
1．（2022·山东菏泽·中考真题）如图，抛物线y=ax2+bx+c(a≠0)与x轴交于A−2,0、B8,0两点，与y轴交于点C0,4，连接AC、BC．
(1)求抛物线的表达式；
(2)将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，直接写出点D的坐标．并求出四边形OADC的面积；
(3)点P是抛物线上的一动点，当∠PCB=∠ABC时，求点P的坐标．
【答案】(1)y=−14x2+32x+4
(2)D−8,8,24
(3)P6,4或343,−1009
【分析】（1）直接利用待定系数法求抛物线解析式即可；
（2）先利用勾股定理的逆定理证明△ABC为直角三角形，再根据折叠的性质得出点B、C、D三点共线，继而通过证明△DBE∼△CBO，利用相似三角形的性质即可得出点D的坐标，根据四边形OADC的面积=S△ADC+S△AOC=S△ABC+S△AOC进行求解即可；
（3）分两种情况讨论：当点P在x轴上方时，当点P在x轴下方时，分别求解即可．
【详解】（1）将A−2,0，B8,0，C0,4代入抛物线y=ax2+bx+c(a≠0)，得
0=4a−2b+c0=64a+8b+c4=c，解得a=−14b=32c=4，
所以，抛物线的表达式为y=−14x2+32x+4；
（2）如图，过点D作DE⊥x轴于E，
∴∠DEB=∠COB=90°，
∵A−2,0，B8,0，C0,4，
∴AB=10,AC=22+42=25,BC=82+42=45,OB=8,OC=4,OA=2，
∵AB2=AC2+BC2，
∴△ABC为直角三角形且∠ACB=90°，
将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，
此时，点B、C、D三点共线，BC=DC，S△ABC=S△ADC，
∵∠DBE=∠CBO，
∴△DBE∼△CBO，
∴DBCB=DEOC=BEBO=2，
∴OB=OE=8,DE=2OC=8，
∴D−8,8，
∴四边形OADC的面积
=S△ADC+S△AOC=S△ABC+S△AOC=12⋅AC⋅BC+12⋅OA⋅OC=12×25×45+12×2×4=24；
（3）
当点P在x轴上方时，
∵∠PCB=∠ABC，
∴CP∥x轴，
∴点P的纵坐标为4，即4=−14x2+32x+4，
解得x=6或0（舍去）
∴P6,4；
当点P在x轴下方时，设直线CP交x轴于F，
∵∠PCB=∠ABC，
∴CF=BF，
设OF=t，则CF=BF=8−t，
在Rt△COF中，由勾股定理得OC2+OF2=CF2，
即42+t2=8−t2，
解得t=3，
∴F3,0，
∵C0,4，
∴设直线CF的解析式为y=kx+4，
即0=3k+4，解得k=−43，
∴直线CF的解析式为y=−43x+4，
令−43x+4=−14x2+32x+4，解得x=343或0（舍去），
当x=343时，y=−14×3432+32×343+4=−1009
∴P343,−1009；
综上，P6,4或343,−1009．
【点睛】本题考查了二次函数的综合题目，涉及待定系数法求二次函数解析式，勾股定理的逆定理，折叠的性质，相似三角形的判定和性质，求一次函数的解析式，等腰三角形的性质等知识，熟练掌握知识点并能够灵活运用是解题的关键．
2．（2022·四川达州·中考真题）如图1，在平面直角坐标系中，已知二次函数y=ax2+bx+2的图象经过点A(−1,0)，B(3,0)，与y轴交于点C．
(1)求该二次函数的表达式；
(2)连接BC，在该二次函数图象上是否存在点P，使∠PCB=∠ABC？若存在，请求出点P的坐标：若不存在，请说明理由；
(3)如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．
【答案】(1)y=−23x2+43x+2
(2)P2,2或285,−28625
(3)163
【分析】（1）待定系数法求解析式即可求解；
（2）根据题意，分情况讨论，①过点C作关于x=1的对称点P，即可求P的坐标，②x轴上取一点D，使得DC=DB，则∠DCB=∠ABC，设Dd,0，根据勾股定理求得CD,BD，建列方程，解方程求解即可；
（3）设Qt,−23t2+43t+2，−1【详解】（1）解：∵由二次函数y=ax2+bx+2，令x=0，则y=2，
∴C0,2，
∵过点A(−1,0)，B(3,0)，
设二次函数的表达式为y=ax+1x−3 =ax2−2x−3，
将点C0,2代入得，
2=−3a，
解得a=−23，
∴y=−23x2+43x+2，
（2）∵二次函数y=ax2+bx+2的图象经过点A(−1,0)，B(3,0)，
∴抛物线的对称轴为x=1，
①如图，过点C作关于x=1的对称点P，
∴CP∥AB，
∴∠PCB=∠ABC，
∵C0,2，
∴P2,2，
②x轴上取一点D，使得DC=DB，则∠DCB=∠ABC，设Dd,0，
则CD=22+d2,BD=3−d，
∴22+d2=3−d2，
解得d=56，
即D56,0，
设直线CD的解析式为y=kx+b，
56k+b=0b=2，
解得k=−125b=2，
∴直线CD的解析式为y=−125x+2，
联立y=−125x+2y=−23x2+43x+2，
解得x=0y=2或x=285y=−28625，
∴P285,−28625，
综上所述，P2,2或285,−28625，
（3）EM+EN的值是定值163，
设Qt,−23t2+43t+2，−1过点Q作QF⊥x轴于点F，则Ft,0，
∵A−1,0,B3,0,E1,0,Ft,0，
∴AE=BE=2,AF=t+1,BF=3−t，
∴ME∥QF,NE∥QF，
∴△AME∽△AQF,△BNE∽△BQF，
∴MEQF=AEAF,NEQF=BEBF，
即MEQF=2t+1,NEQF=23−t，
∴ME=2t+1QF，NE=23−tQF，
∴ME+NE=2t+1+23−tQF，
∵QF=−23t2+43t+2=−23×t+1t−3，
∴ME+NE=2t+1+23−t×−23×t+1t−3
=−43t−3−t+1
=163．
即EM+EN的值是定值163
【点睛】本题考查了二次函数综合，待定系数法求解析式，角度问题，相似三角形的性质与判定，掌握二次函数的性质是解题的关键．
类型九 二倍角、半角存在性问题
【构造二倍角的方法】
方法一：构造二倍角的三角函数，并通过勾股定理求解.（左图）
方法二：等腰三角形的外角.（右图）

把2倍角转化为角相等的常用方法
1) 利用角平分线转化；
2) 利用等腰三角形顶角的外角转化；
3) 利用直角三角形斜边中线得等腰三角形转化.
1．（2020·辽宁鞍山·中考真题）在平面直角坐标系中，抛物线y=ax2+bx+2(a≠0)经过点A(−2,−4)和点C(2,0)，与y轴交于点D，与x轴的另一交点为点B．
（1）求抛物线的解析式；
（2）如图1，连接BD，在抛物线上是否存在点P，使得∠PBC=2∠BDO？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，连接AC，交y轴于点E，点M是线段AD上的动点（不与点A，点D重合），将△CME沿ME所在直线翻折，得到△FME，当△FME与△AME重叠部分的面积是△AMC面积的14时，请直接写出线段AM的长．
【答案】（1）y=−x2+x+2；（2）存在，（23，209）或（103，−529）；（3）6105或22
【分析】（1）根据点A和点C的坐标，利用待定系数法求解；
（2）在x轴正半轴上取点E，使OB=OE，过点E作EF⊥BD，垂足为F，构造出∠PBC=∠BDE，分点P在第三象限时，点P在x轴上方时，点P在第四象限时，共三种情况分别求解；
（3）设EF与AD交于点N，分点F在直线AC上方和点F在直线AC下方时两种情况，利用题中所给面积关系和中线的性质可得MN=AN，FN=NE，从而证明四边形FMEA为平行四边形，继而求解．
【详解】解：（1）∵抛物线y=ax2+bx+2(a≠0)经过点A（-2，-4）和点C（2，0），
则−4=4a−2b+20=4a+2b+2，解得：a=−1b=1，
∴抛物线的解析式为y=−x2+x+2；
（2）存在，理由是：
在x轴正半轴上取点E，使OB=OE，过点E作EF⊥BD，垂足为F，
在y=−x2+x+2中，
令y=0，解得：x=2或-1，
∴点B坐标为（-1，0），
∴点E坐标为（1，0），
可知：点B和点E关于y轴对称，
∴∠BDO=∠EDO，即∠BDE=2∠BDO，
∵D（0，2），
∴DE=22+12=5=BD，
在△BDE中，有12×BE×OD=12×BD×EF，
即2×2=5×EF，解得：EF=455，
∴DF=DE2−EF2=355，
∴tan∠BDE=EFDF=455÷355=43，
若∠PBC=2∠BDO，
则∠PBC=∠BDE，
∵BD=DE=5，BE=2，
则BD2+DE2＞BE2，
∴∠BDE为锐角，
当点P在第三象限时，
∠PBC为钝角，不符合；
当点P在x轴上方时，
∵∠PBC=∠BDE，设点P坐标为（c，−c2+c+2），
过点P作x轴的垂线，垂足为G，
则BG=c+1，PG=−c2+c+2，
∴tan∠PBC=PGBG=−c2+c+2c+1=43，
解得：c=23，
∴−c2+c+2=209，
∴点P的坐标为（23，209）；
当点P在第四象限时，
同理可得：PG=c2−c−2，BG=c+1，
tan∠PBC=PGBG=c2−c−2c+1=43，
解得：c=103，
∴−c2+c+2=−529，
∴点P的坐标为（103，−529），
综上：点P的坐标为（23，209）或（103，−529）；
（3）设EF与AD交于点N，
∵A（-2，-4），D（0，2），设直线AD表达式为y=mx+n，
则−4=−2m+n2=n，解得：m=3n=2，
∴直线AD表达式为y=3x+2，
设点M的坐标为（s，3s+2），
∵A（-2，-4），C（2，0），设直线AC表达式为y=m1x+n1，
则−4=−2m1+n10=2m1+n1，解得：m1=1n1=−2，
∴直线AC表达式为y=x-2，
令x=0，则y=-2，
∴点E坐标为（0，-2），
可得：点E是线段AC中点，
∴△AME和△CME的面积相等，
由于折叠，
∴△CME≌△FME，即S△CME=S△FME，
由题意可得：
当点F在直线AC上方时，
∴S△MNE=14S△AMC=12S△AME=12S△FME，
即S△MNE= S△ANE= S△MNF，
∴MN=AN，FN=NE，
∴四边形FMEA为平行四边形，
∴CM=FM=AE=12AC=12×42+42=22，
∵M（s，3s+2），
∴s−22+3s+22=22，
解得：s=−45或0（舍），
∴M（−45，−25），
∴AM=−45+22+−25+42=6105，
当点F在直线AC下方时，如图，
同理可得：四边形AFEM为平行四边形，
∴AM=EF，
由于折叠可得：CE=EF，
∴AM=EF=CE=22，
综上：AM的长度为6105或22．
【点睛】本题是二次函数综合题，涉及到待定系数法，二次函数的图像和性质，折叠问题，平行四边形的判定和性质，中线的性质，题目的综合性很强．难度很大，对学生的解题能力要求较高．
2．（2020·湖南张家界·中考真题）如图，抛物线y=ax2−6x+c交x轴于A,B两点，交y轴于点C．直线y=−x+5经过点B,C．
（1）求抛物线的解析式；
（2）抛物线的对称轴l与直线BC相交于点P，连接AC,AP，判定△APC的形状，并说明理由；
（3）在直线BC上是否存在点M，使AM与直线BC的夹角等于∠ACB的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．
【答案】（1）y=x2−6x+5；（2）△APC的为直角三角形，理由见解析；（3）存在使AM与直线BC的夹角等于∠ACB的2倍的点，且坐标为M1（136,176），M2（236，76）．
【分析】（1）先根据直线y=−x+5经过点B,C，即可确定B、C的坐标，然后用带定系数法解答即可；
（2）先求出A、B的坐标结合抛物线的对称性，说明三角形APB为等腰三角形；再结合OB=OC得到∠ABP=45°，进一步说明∠APB=90°，则∠APC=90°即可判定△APC的形状；
（3）作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，AC于E；然后说明△ANB为等腰直角三角形，进而确定N的坐标；再求出AC的解析式，进而确定M1E的解析式；然后联立直线BC和M1E的解析式即可求得M1的坐标；在直线BC上作点M1关于N点的对称点M2，利用中点坐标公式即可确定点M2的坐标
【详解】解：（1）∵直线y=−x+5经过点B,C
∴当x=0时，可得y=5，即C的坐标为（0,5）
当y=0时，可得x=5，即B的坐标为（5,0）
∴5=a⋅02−6×0+c0=52a−6×5+c解得a=1c=5
∴该抛物线的解析式为y=x2−6x+5
（2）△APC的为直角三角形，理由如下：
∵解方程x2−6x+5=0，则x1=1，x2=5
∴A（1,0），B（5,0）
∵抛物线y=x2−6x+5的对称轴l为x=3
∴△APB为等腰三角形
∵C的坐标为（5,0）, B的坐标为（5,0）
∴OB=CO=5,即∠ABP=45°
∴∠ABP=45°，
∴∠APB=180°-45°-45°=90°
∴∠APC=180°-90°=90°
∴△APC的为直角三角形；
（3）如图：作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，AC于E，
∵M1A=M1C，
∴∠ACM1=∠CAM1
∴∠AM1B=2∠ACB
∵△ANB为等腰直角三角形.
∴AH=BH=NH=2
∴N（3，2）
设AC的函数解析式为y=kx+b
∵C(0，5),A(1，0)
∴5=k⋅0+b0=k+b 解得b=5，k=-5
∴AC的函数解析式为y=-5x+5
设EM1的函数解析式为y=15x+n
∵点E的坐标为（12,52）
∴52=15×12 +n，解得：n=125
∴EM1的函数解析式为y=15x+125
∵y=−x+5y=15x+125 解得x=136y=176
∴M1的坐标为（136,176）；
在直线BC上作点M1关于N点的对称点M2
设M2（a，-a+5）
则有：3=136+a2，解得a=236
∴-a+5=76
∴M2的坐标为（236，76）．
综上，存在使AM与直线BC的夹角等于∠ACB的2倍的点，且坐标为M1（136,176），M2（236，76）．
【点睛】本题属于二次函数与几何的综合题，主要考查了待定系数法确定函数解析式、等腰直角三角形的判定与性质、一次函数图像、三角形外角等知识，考查知识点较多，综合应用所学知识成为解答本题的关键．
3．（2021·山东泰安·中考真题）二次函数y=ax2+bx+4(a≠0)的图象经过点A(−4,0)，B(1,0)，与y轴交于点C，点P为第二象限内抛物线上一点，连接BP、AC，交于点Q，过点P作PD⊥x轴于点D．
（1）求二次函数的表达式；
（2）连接BC，当∠DPB=2∠BCO时，求直线BP的表达式；
（3）请判断：PQQB是否有最大值，如有请求出有最大值时点P的坐标，如没有请说明理由．
【答案】（1）y=−x2−3x+4；（2）y=−158x+158；（3）PQQB有最大值为45，P点坐标为(−2,6)
【分析】（1）将A(−4,0)，B(1,0)代入y=ax2+bx+4(a≠0)中，列出关于a、b的二元一次方程组，求出a、b的值即可；
（2）设BP与y轴交于点E，根据PD//y轴可知，∠DPB=∠OEB，当∠DPB=2∠BCO，即∠OEB=2∠BCO，由此推断△OEB为等腰三角形，设OE=a，则CE=4−a，所以BE=4−a，由勾股定理得BE2=OE2+OB2，解出点E的坐标，用待定系数法确定出BP的函数解析式即可；
（3）设PD与AC交于点N，过B作y轴的平行线与AC相交于点M．由A、C两点坐标可得AC所在直线表达式，求得 M点坐标，则BM=5，由BM//PN，可得△PNQ∽△BMQ，PQQB=PNBM=PN5，设P(a0,−a02−3a0+4)(−4【详解】解：（1）由题意可得：
a⋅(−4)2+b⋅(−4)+4=0a+b+4=0
解得：a=−1b=−3，
∴二次函数的表达式为y=−x2−3x+4；
（2）设BP与y轴交于点E，
∵PD//y轴，
∴∠DPB=∠OEB，
∵∠DPB=2∠BCO，
∴∠OEB=2∠BCO，
∴∠ECB=∠EBC，
∴BE=CE，设OE=a，
则CE=4−a，∴BE=4−a，
在Rt△BOE中，由勾股定理得BE2=OE2+OB2，
∴(4−a)2=a2+12
解得a=158，
∴E0,158，
设BE所在直线表达式为y=kx+e(k≠0)
∴k⋅0+e=158,k⋅1+e=0.解得k=−158,e=158.
∴直线BP的表达式为y=−158x+158．
（3）设PD与AC交于点N．
过B作y轴的平行线与AC相交于点M．
由A、C两点坐标分别为(−4,0)，(0,4)
可得AC所在直线表达式为y=x+4
∴M点坐标为(1,5)，BM=5
由BM//PN，可得△PNQ∽△BMQ，
∴PQQB=PNBM=PN5
设P(a0,−a02−3a0+4)(−4∴PQQB=−a02−3a0+4−(a0+4)5=−a02−4a05=−(a0+2)2+45，
∴当a0=−2时，PQQB有最大值0.8，
此时P点坐标为(−2,6)．
【点睛】本题主要考查二次函数以及一次函数解析式的确定，函数图像的性质，相似三角形，勾股定理等知识点，熟练运用待定系数法求函数解析式是解题关键，本题综合性强，涉及知识面广，难度较大，属于中考压轴题．
4．（2020·内蒙古鄂尔多斯·中考真题）如图1，抛物线y＝x2+bx+c交x轴于A，B两点，其中点A的坐标为(1，0)，与y轴交于点C（(0，﹣3)．
（1）求抛物线的函数解析式；
（2）点D为y轴上一点，如果直线BD与直线BC的夹角为15°，求线段CD的长度；
（3）如图2，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO，求点P的坐标．

【答案】（1）y＝x2+2x﹣3；（2）CD的长度为3﹣3或33﹣3；（3）(﹣154，5716)，(﹣94，﹣3916)
【分析】（1）将点A，点C坐标代入解析式可求解；
（2）先求出点B坐标，可得OB＝OC，可得∠OBC＝∠OCB＝45°，再分点D在点C上方或下方两种情况讨论，由锐角三角函数可求解；
（3）在BO上截取OE＝OA，连接CE，过点E作EF⊥AC，由“SAS”可证△OCE≌△OCA，可得∠ACO＝∠ECO，CE＝AC＝10，由面积法可求EF的长，由勾股定理可求CF的长，可求tan∠ECA＝tan∠PAB＝34，分点P在AB上方和下方两种情况讨论，求出AP解析式，联立方程组可求点P坐标．
【详解】解：（1）∵抛物线y＝x2+bx+c交x轴于点A（1，0），与y轴交于点C（0，﹣3），
∴0=1+b+cc=−3，
解得：b=2c=−3，
∴抛物线解析式为：y＝x2+2x﹣3；
（2）∵抛物线y＝x2+2x﹣3与x轴于A，B两点，
∴点B（﹣3，0），
∵点B（﹣3，0），点C（0，﹣3），
∴OB＝OC＝3，
∴∠OBC＝∠OCB＝45°，
如图1，当点D在点C上方时，

∵∠DBC＝15°，
∴∠OBD＝30°，
∴tan∠DBO＝ODBO＝33，
∴OD＝33×3＝3，
∴CD＝3﹣3；
若点D在点C下方时，
∵∠DBC＝15°，
∴∠OBD＝60°，
∴tan∠DBO＝ODBO＝3，
∴OD＝33，
∴DC＝33﹣3，
综上所述：线段CD的长度为3﹣3或33﹣3；
（3）如图2，在BO上截取OE＝OA，连接CE，过点E作EF⊥AC，

∵点A（1，0），点C（0，﹣3），
∴OA＝1，OC＝3，
∴AC＝OA2+OC2＝1+9＝10，
∵OE＝OA，∠COE＝∠COA＝90°，OC＝OC，
∴△OCE≌△OCA（SAS），
∴∠ACO＝∠ECO，CE＝AC＝10，
∴∠ECA＝2∠ACO，
∵∠PAB＝2∠ACO，
∴∠PAB＝∠ECA，
∵S△AEC＝12AE×OC＝12AC×EF，
∴EF＝2×310＝3105，
∴CF＝CE2−EF2＝10−185＝4105，
∴tan∠ECA＝EFCF＝34，
如图2，当点P在AB的下方时，设AO与y轴交于点N，
∵∠PAB＝∠ECA，
∴tan∠ECA＝tan∠PAB＝ONAO＝34，
∴ON＝34，
∴点N（0，34），
又∵点A（1，0），
∴直线AP解析式为：y＝34x﹣34，
联立方程组得：y=34x−34y=x2+2x−3，
解得：x1=1y1=0或x2=−94y2=−3916，
∴点P坐标为：（﹣94，﹣3916）
当点P在AB的上方时，同理可求直线AP解析式为：y＝﹣34x+34，
联立方程组得：y=−34x+34y=x2+2x−3，
解得：x1=1y1=0或x2=−154y2=5716，
∴点P坐标为：（﹣154，5716），
综上所述：点P的坐标为（﹣154，5716），（﹣94，﹣3916）．
【点睛】本题是二次函数综合题，考查了待定系数法求解析式，全等三角形的判定和性质，直角三角形的性质，锐角三角函数等知识，求出tan∠ECA=tan∠PAB=34是本题的关键．
类型十 特殊角存在性问题
1．（2022·湖北黄石·中考真题）如图，抛物线y=−23x2+23x+4与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点且横坐标为m．
(1)A，B，C三点的坐标为____________，____________，____________；
(2)连接AP，交线段BC于点D，
①当CP与x轴平行时，求PDDA的值；
②当CP与x轴不平行时，求PDDA的最大值；
(3)连接CP，是否存在点P，使得∠BCO+2∠PCB=90°，若存在，求m的值，若不存在，请说明理由．
【答案】(1)A−2,0;B3,0;C0,4
(2)①15；②940
(3)存在点P，m=74
【分析】(1)令x=0，则y=4，令y=0，则−23x2+23x+4=0，所以x=-2或x=3，由此可得结论；
(2)①由题意可知，P(1，4)，所以CP=1，AB=5，由平行线分线段成比例可知，PDDA=CPAB=15．
②过点P作PQ∥AB交BC于点Q，所以直线BC的解析式为：y=-43x+4．设点P的横坐标为m，则P(m，-23m2+23m+4)，Q(12m2−12m，-23m2+23m+4)．所以PQ=m-(12m2−12m)=-12m2+32m，因为PQ∥AB，所以PDDA=PQAB=−12m2+32m5=−110(m−32)2+940，由二次函数的性质可得结论；
(3)假设存在点P使得∠BCO+2∠BCP=90°，即0＜m＜3．过点C作CF∥x轴交抛物线于点F，由∠BCO+2∠PCB=90°，可知CP平分∠BCF，延长CP交x轴于点M，易证△CBM为等腰三角形，所以M(8，0)，所以直线CM的解析式为：y=-12x+4，令−23x2+23x+4=-12x+4，可得结论．
【详解】（1）解：令x=0，则y=4，
∴C(0，4)；
令y=0，则−23x2+23x+4=0，
∴x=-2或x=3，
∴A(-2，0)，B(3，0)．
故答案为：(-2，0)；(3，0)；(0，4)．
（2）解：①∵CP∥x轴，C0,4，
∴P1,4，CP=1，AB=5
又∵CP∥x轴，
∴△CPD∽△BAD
∴PDDA=CPAB=15；
②过P作PQ∥AB交BC于点Q，
设直线BC的解析式为y=k1x+b1，
把B(3，0)，C(0，4)代入，得
3k1+b1=0b1=4，解得k1=−43b1=4，
∴直线BC的解析式为y=−43x+4，
设Pm,−23m2+23m+4，则Q12m2−12m,−23m2+23m+4，
∴PQ=m−12m2−12m=−12m2+32m，
∵PQ∥AB，
∴△QPD∽△BAD
∴PDDA=PQAB=−12m2+32m5=−110m−322+940，
∴当m=32时，PDDA取最大值940；
（3）解：假设存在点P使得∠BCO+2∠BCP=90°，即0过C作CF∥x轴，连接CP，延长CP交x轴于点M，
∴∠FCP=∠BMC，
∵∠BCO+2∠BCP=90°，
∴CP平分∠BCF，
∴∠BCP=∠FCP，
∴∠BCP=∠BMC，
∴BC=BM，
∴△CBM为等腰三角形，
∵BC=5，
∴BM=5，OM=8，M8,0，
设直线CM解析式为y=kx+b，
把C(0，4)，M8,0代入，得
8k+b=0b=4，解得：k=−12b=4，
∴直线CM的解析式为y=−12x+4，
联立y=−12x+4y=−23x2+23x+4，
解得x=74或x=0(舍)，
∴存在点P满足题意，即m=74．
【点睛】此题是二次函数综合题，主要考查了待定系数法，平行线分线段成比例，角度的存在性等相关内容，解本题的关键是求抛物线解析式，确定点P的坐标．
2．（2023·四川自贡·中考真题）如图，抛物线y=−43x2+bx+4与x轴交于A(−3,0)，B两点，与y轴交于点C．

(1)求抛物线解析式及B，C两点坐标；
(2)以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；
(3)该抛物线对称轴上是否存在点E，使得∠ACE=45°，若存在，求出点E的坐标；若不存在，请说明理由．
【答案】(1)抛物线解析式为y=−43x2−83x+4，B1,0，C0,4
(2)D−2,−4或D−4,4或D4,4
(3)E−1,277
【分析】
（1）将点A(﹣3,0)代入抛物线解析式，待定系数法求解析式，进而分别令x,y=0，即可求得B,C两点的坐标；
（2）分三种情况讨论，当AB，AC,BC为对角线时，根据中点坐标即可求解；
（3）根据题意，作出图形，作AG⊥CE交于点G，F为AC的中点，连接GO,GF，则A,O,C,G在⊙F上，根据等弧所对的圆周角相等，得出G在y=−x上，进而勾股定理，根据FG=52建立方程，求得点G的坐标，进而得出CG的解析式，即可求解．
【详解】（1）解：∵抛物线y=−43x2+bx+4与x轴交于A(−3,0)，
∴−43×−32−3b+4=0
解得：b=−83，
∴抛物线解析式为y=−43x2−83x+4，
当x=0时，y=4，
∴C0,4，
当y=0时，0=−43x2−83x+4
解得：x1=−3,x2=1，
∴B1,0
（2）∵A(−3,0)，B1,0，C0,4，
设Dm,n，
∵以A，B，C，D为顶点的四边形是平行四边形
当AB为对角线时，m+02=−3+12,4+n2=0+02
解得：m=−2,n=−4，
∴D−2,−4；
当AC为对角线时，−3+02=1+m2,4+02=0+n2
解得：m=−4,n=4
∴D−4,4
当BC为对角线时，−3+m2=0+12,0+42=0+n2
解得：m=4,n=4
∴D4,4
综上所述，以A，B，C，D为顶点的四边形是平行四边形，D−2,−4或D−4,4或D4,4
（3）解：如图所示，作AG⊥CE交于点G，F为AC的中点，连接GO,GF，

∵∠ACE=45°
∴△AGC是等腰直角三角形，
∴A,O,C,G在⊙F上，
∵A(−3,0)，C0,4，
∴F−32,2，AC=AO2+CO2=5，GF=12AC=52
∵∠AOG=∠ACG=45°，
∴G在y=−x上，
设Gt,−t，则GF2=t+322+−t−22=522
解得：t1=−72，t2=0（舍去）
∴点G−72，72
设直线CG的解析式为y=kx+4
∴72=−72k+4
解得：k=17.
∴直线CG的解析式y=17x+4
∵A(−3,0)，B1,0，
∴抛物线对称轴为直线x=−3+12=−1，
当x=−1时，17×−1+4=277，
∴E−1,277．
【点睛】本题考查了二次函数的综合运用，待定系数法求解析式，平行四边形的性质，圆周角角定理，勾股定理，求一次函数解析式，熟练掌握以上知识是解题的关键．
3．（2021·山东烟台·中考真题）如图，抛物线y=ax2+bx+c经过点A−2,0，B4,0，与y轴正半轴交于点C，且OC=2OA．抛物线的顶点为D，对称轴交x轴于点E．直线y=mx+n经过B，C两点．
（1）求抛物线及直线BC的函数表达式；
（2）点F是抛物线对称轴上一点，当FA+FC的值最小时，求出点F的坐标及FA+FC的最小值；
（3）连接AC，若点P是抛物线上对称轴右侧一点，点Q是直线BC上一点，试探究是否存在以点E为直角顶点的Rt△PEQ，且满足tan∠EQP=tan∠OCA．若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）y=−12x2+x+4，y=−x+4；（2）F点坐标为（1，3）；FA+FC的最小值为42；（3）P点坐标为(7，12+7)或(13，−52+13)；
【分析】（1）求出C点坐标，再用待定系数法求二次函数和一次函数解析式即可；
（2）根据对称性可知，FA=FB，当B、F、C三点共线时，FA+FC的值最小，即点F为BC与对称轴交点，利用解析式和勾股定理可求坐标和最小值；
（3）作QM⊥DE于M，PN⊥DE与N，证△MQE∽△NEP，设点P坐标，利用相似比表示出Q点坐标，代入y=−x+4即可．
【详解】解：（1）∵A−2,0，
∴OC=2OA=4，C点坐标为（0,4），
∵抛物线y=ax2+bx+c经过点A−2,0，B4,0，可设解析式为y=a(x+2)(x−4)，
把（0,4）代入，得4=a(0+2)(0−4)，
解得，a=−12，
抛物线解析式为y=−12(x+2)(x−4)，即y=−12x2+x+4，
设BC的解析式为y=kx+n，把B4,0，（0,4）代入，
得0=4k+n4=n，解得k=−1n=4，
∴BC的解析式为y=−x+4；
（2）∵点F是抛物线对称轴上一点，
∴FA=FB，当B、F、C三点共线时，FA+FC的值最小，最小值为BC长，此时，点F为BC与对称轴交点，
抛物线y=−12x2+x+4的对称轴为直线x=−12×(−12)=1，
把x=1代入y=−x+4，得y=3，
则F点坐标为（1，3）；
BC=OC2+OB2=42，即FA+FC的最小值为42；
（3）由（1）得，tan∠EQP=tan∠OCA=12，即EPQE=12，
作QM⊥DE于M，PN⊥DE与N，
∵∠QEP=90°，
∴∠QEM+∠MQE=90°，∠QEM+∠PEN=90°，
∴∠MQE=∠PEN，
∴△MQE∽△NEP，
∴QMEN=MEPN=QEEP=2，
如图1，设P点坐标为(m，−12m2+m+4)，
则PN=m−1，EN=−12m2+m+4，EM=2m−2，MQ=−m2+2m+8，
则Q点坐标为(−m2+2m+9，2−2m)，
代入y=−x+4，得2−2m=m2−2m−9+4，
解得，m1=7，m2=−7（舍去），
把m1=7代入y=−12x2+x+4，得，y=12+7，
故P点坐标为(7，12+7)；
如图2，设P点坐标为(m，−12m2+m+4)，
则PN=m−1，EN=−12m2+m+4，EM=2m−2，MQ=−m2+2m+8，
则Q点坐标为(m2−2m−7，2m−2)，
代入y=−x+4，得2m−2=−m2+2m+7+4，
解得，m1=13，m2=−13（舍去），
把m1=13代入y=−12x2+x+4，得，y=−52+13，
故P点坐标为(13，−52+13)；
综上，P点坐标为(7，12+7)或(13，−52+13)；
【点睛】本题考查了二次函数的综合，包括解直角三角形、最短路径和直角三角形存在性问题，解题关键是熟练运用二次函数知识，设出点的坐标，利用相似三角形的判定与性质表示出其他点的坐标，列出方程．
1．（2024·湖北省直辖县级单位·一模）抛物线y=x2−4x与直线y=x交于原点O和点B，与x轴交于另一点A，顶点为D．
(1)求出点B和点D的坐标；
(2)如图①，连接OD，P为x轴的负半轴上的一点，当tan∠PDO=12时，求点P的坐标；
(3)如图②，M是点B关于抛物线的对称轴的对称点，Q是抛物线上的动点，它的横坐标为m0【答案】(1)B5,5，D2,−4
(2)P−103,0
(3)2524
【分析】（1）令y=x2−4x=x，可求出点B的坐标，将函数y=x2−4x化为顶点式，可求出点D的坐标；
（2）过点D作DE⊥y轴于点E，可得tan∠DOE=12，推出∠DOE=∠PDO，由点P为x轴的负半轴上的一点，设直线DP与y轴交于点G，则△ODG是等腰三角形，可得OG=DG，设OG=t，则DG=t，GE=4−t，根据勾股定理求出t值，进而得到点G的坐标，利用待定系数法求出直线DG的解析式，即可求解；
（3）分别过点M，Q作y轴的平行线，交直线OB于点N，K，则S1=12QKxB−xE，S2=12MNxB−xE，由点P的横坐标为m，可表达S1S2，利用二次函数的性质可得结论．
【详解】（1）解：令y=x2−4x=x，
解得x=0或x=5，
∴ B5,5；
∵ y=x2−4x=x−22−4，
∴顶点D2,−4；
（2）如图，过点D作DE⊥y轴于点E，
∴ DE=2，OE=4，
∴ tan∠DOE=12，
∵ tan∠PDO=12，
∴ ∠DOE=∠PDO，
∵ P为x轴的负半轴上的一点，设直线DP与y轴交于点G，则△ODG是等腰三角形，
∴ OG=DG，
设OG=t，则DG=t，GE=4−t，
在Rt△DGE中，t2=22+4−t2，
解得：t=52，
∴ G0,−52，
设直线DG的解析式为：y=kx+b，将点D2,−4、G0,−52代入得：
2k+b=−40+b=−52，
解得：k=−34b=−52，
∴直线DG的解析式为：y=−34x−52，
令y=0，则−34x−52=0，
解得：x=−103，
∴ P−103,0；
（3）∵点B5,5与点M关于对称轴x=2对称，
∴ M−1,5，
如图，分别过点M，Q作y轴的平行线，交直线OB于点N，K，
∴ N−1,−1，MN=6，
∵点Q横坐标为m，
∴ Qm,m2−4m，Km,m，
∴ KQ=m−m2−4m=−m2+5m，
∵ S1=12QKxB−xE，S2=12MNxB−xE，
∴ S1S2=QKMN=−16m2−5m=−16m−522+2524=，
∵ −16<0，
∴当m=52时，S1S2的最大值为2524．
【点睛】本题考查了二次函数的综合应用，涉及二次函数的性质，三角形的面积，一次函数，解直角三角形等知识，解题的关键是灵活运用这些知识．
2．（2024·四川·模拟预测）如图，已知二次函数的图象过点O0，0,A8，4，与x轴交于另一点B，且对称轴是直线x=3．
(1)求该二次函数的解析式；
(2)若M是OB上的一点，作MN∥AB交OA于N，当△ANM面积最大时，求M的坐标；
(3)P是x轴上的点，过P作PQ⊥x轴与抛物线交于Q．过A作AC⊥x轴于C，当以O，P，Q为顶点的三角形与以O，A，C为顶点的三角形相似时，求P点的坐标．
【答案】(1)y=14x2−32x；
(2)M3,0；
(3)P点坐标为14,0或−2,0或4,0或8,0．
【分析】
（1）先根据对称轴求出点B的坐标，然后将抛物线设成交点式，再将点A代入求解即可；
（2）设Mt,0，先用待定系数法求出直线OA和直线AB的解析式，然后根据MN∥AB求出直线MN的解析式，再利用直线OA与直线MN联立求出N的坐标，然后利用S△AMN=S△AOM−S△MON求出面积的最大值及此时t的值，进而可求出M的坐标；
（3）设P(m,0),Qm,14m2−32m，分两种情况：当PQOC=POAC时，△PQO∽△COA，即PQ8=PO4；当PQAC=POOC时，△PQO∽△CAO，即PQ4=PO3，分别建立关于m的方程求解即可得出m的值，进而可求P的坐标．
【详解】（1）解：∵抛物线过原点，对称轴是直线x=3，
∴B点坐标为6,0．
设抛物线解析式为y=axx−6，
把A8,4代入得a×8×2=4，
解得a=14，
∴抛物线解析式为y=14xx−6，
即y=14x2−32x；
（2）解：设Mt,0，
设直线OA的解析式为y=fx，
把A8,4代入得8f=4，
解得f=12，
∴直线OA的解析式为y=12x．
设直线AB的解析式为y=kx+b，
把B6,0,A8,4代入得
6k+b=08k+b=4，解得k=2b=−12，
∴直线AB的解析式为y=2x−12．
∵MN∥AB，
∴设直线MN的解析式为y=2x+n，
把Mt,0代入得2t+n=0，解得n=−2t，
∴直线MN的解析式为y=2x−2t．
将直线OA与直线MN方程联立得，
y=12xy=2x−2t
解得x=43ty=23t，
∴N43t,23t，
∴S△AMN=S△AOM−S△MON =12×4×t−12×t×23t=−13t2+2t=−13t−32+3，
当t=3时，S△AMN有最大值3，
∴M3,0；
（3）解：设P(m,0),Qm,14m2−32m，
∵∠OPQ=∠ACO，
当PQOC=OPAC时，△PQO∽△COA，即PQ8=OP4，
∴PQ=2PO，即14m2−32m=2m，
则14m2−32m=2m，得m1=0（舍去），m2=14，此时P点坐标为14,0，
或14m2−32m=−2m得m1=0（舍去），m2=−2，此时P点坐标为−2,0；
当PQAC=POOC时，ΔPQO∽ΔCAO，即PQ4=PO3，
∴PQ=12PO，即14m2−32m=12m，
则14m2−32m=12m得m1=0（舍去），m2=8，
或14m2−32m=−12m得m1=0（舍去），m2=4，
此时P点坐标为4,0或8,0；
综上所述，P点坐标为14,0或−2,0或4,0或8,0．
【点睛】本题主要考查二次函数与几何综合，掌握待定系数法，相似三角形的判定及性质，一元二次方程的解法，二次函数的图象和性质是解题的关键．
3．（2024·江苏扬州·模拟预测）如图，抛物线y=−x2+bx+c经过A−1,0，C0,3两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．
(1)求该抛物线与直线AM的表达式；
(2)若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；
(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．
【答案】(1)抛物线的表达式：y=−x2+2x+3，直线AM的表达式：y=2x+2；
(2)MH+DH=37；
(3)Q点坐标为1,3或1,1或1,5．
【分析】
本题考查了一次函数和二次函数的图像和性质，待定系数法求解析式，二次函数的应用等知识；
（1）先将A、C点坐标代入解析式，求出二次函数解析式，然后再求出抛物线顶点M的坐标，再根据待定系数法求出一次函数解析式；
（2）作D点关于x轴的对称点D'，连接D'M交x轴与点H，则此时MH+DH的值最小，最小值为D'M，求出D'M的值即可；
（3）分DM、DP、MP分别为对角线，三种情况进行讨论求解即可．
【详解】（1）解：将A−1,0，C0,3代入二次函数解析式有：
−1−b+c=0c=3
解得b=2，
∴抛物线的解析式为：y=−x2+2x+3，
有y=−(x−1)2+4，
M点坐标：(1,4)，
设直线AM的解析式为y=kx+b，则有：
−k+b=0k+b=4，
解得：k=2b=2
∴直线AM的解析式为：y=2x+2．
（2）解：作D点关于x轴的对称点D'，连接D'M交x轴与点H，连接DH则此时MH+DH的值最小；
∵MH+DH=MH+D'H≥D'M,
∴当D'、H、M三点共线时，MH+DH取最小值D'M，
∵y=2x+2中，另x=0，则y=2，
∴D(0,2)，D'(0，−2)，
∴D'M=12+(4+2)2=37,
即：MH+DH取最小值为37；
（3）解：存在，
∵y=−(x−1)2+4，
∴对称轴为直线x=1，
设P(p,t)，Q(1,n)，
当以D、M、P、Q为顶点的四边形是平行四边形时：
当DM为对角线时，有：
1+p=0+1t+n=4+2
∴p=4t+n=6，
当p=0时，t=3，
∴n=3，
∴Q点坐标为(1,3)
当DP为对角线时，，
0+p=1+12+t=4+n，
∴p=22+t=4+n，
当p=2时，t=22+2×2=3，
∴n=1，
∴此时Q点坐标为(1,1)；
当MP为对角线时：
有1+p=1+04+t=2+n，
∴p=0n+t=2，
当p=0时，t=3，
∴n=5，
∴Q点坐标为(1,5)；
综上，当以D，M，P，Q为顶点的四边形是平行四边形时，Q点的坐标为1,3或1,1或1,5．
【点睛】本题考查二次函数的综合应用，是中考常见的压轴题．正确的求出函数解析式，熟练掌握二次函数的性质，利用数形结合和分类讨论的思想进行求解，是解题的关键．
4．（2024·湖南·一模）如图，O为坐标原点，抛物线C1:y=−14x2−ax与x轴交于M(−4,0)，顶点为A．
(1)如图1，求直线AM的函数解析式；
(2)如图1，将直线AM绕点M顺时针旋转45°得到直线MN并交抛物线C1于点N，若Q为x轴上一点，求5NQ+5MQ的最小值；
(3)如图2，将抛物线C1平移得到C2，顶点由A平移到B(4,b)，若点B在直线AM上，点D和E分别在抛物线C1和C2上，那么四边形ADEB是否可以为菱形？若可以，求出D点坐标，若不可以，说明理由．
【答案】(1)y=12x+2
(2)8059
(3)可以，点D坐标为25−2,−4或−25−2,−4
【分析】（1）将M(−4,0)代入y=−14x2−ax可求出a，化成顶点式求出A−2,1，由待定系数法，即可求解；
（2）过C作CD⊥MN交于D，过Q作QE⊥AM交于E，由勾股定理得CM=OC2+OM2可求出CM的长，由正弦函数得CD=CM⋅sin∠CMD， sin∠CMO=OCMC求出CD及三角函数值，设G0,m，由勾股定理得MG=OM2+OG2，由三角形面积12CG⋅OM=12MG⋅CD可求出G的坐标，从而可求N的坐标，而5NQ+5MQ =5NQ+EQ，当N、Q、E三点共线时5NQ+5MQ取得最小值，即可求解；
（3）设Dn,−14n2−n，由勾股定理求得AD=AB =35，即n+22+−14n2−n−12=35，解方程，即可求解．
【详解】（1）解：将M(−4,0)代入y=−14x2−ax得，
−14×−42+4a=0，
解得：a=1，
∴ y=−14x2−x =−14x+22+1，
∴ A−2,1，
设直线AM的函数解析式为y=kx+b，
则有−2k+b=1−4k+b=0，
解得：k=12b=2，
故直线AM的函数解析式为y=12x+2；
（2）解：如图，过C作CD⊥MN交于D，过Q作QE⊥AM交于E，
当x=0时，y=12x+2=2，
∴C0,2，
∴CM=OC2+OM2 =22+42 =25，
∵∠CMD=45°，
∴CD=CM⋅sin∠CMD =25×22 =10，
∴sin∠CMO=OCMC =225=55，
设G0,m，
∴MG=OM2+OG2 =16+m2，
∵12CG⋅OM=12MG⋅CD，
∴122−m×4=12×10×16+m2
整理得：3m2−32m−48=0，
解得：m1=−43，m2=12(舍去)，
∴ G0,−43，
设直线MN的解析式为y=k1x+b1，则有−4k1+b1=0b1=−43，
解得：k1=−13b1=−43，
∴直线MN的解析式为y=−13x−43，
联立y=−13x−43y=−14x2−x，
解得：x1=−4y1=0，x2=43y2=−169，
∴N43,−169，
∴MN=43+42+−1692 =16910，
∴ 5NQ+5MQ =5NQ+55MQ =5NQ+MQ⋅sin∠CMO =5NQ+EQ，
∴当N、Q、E三点共线时，5NQ+5MQ取得最小值，
此时，如图，
∴ 5NQ+5MQ =5MN⋅sin45° =5×16910×22 =8095；
故5NQ+5MQ的最小值为8095；
（3）解：可以，理由如下：

∵顶点由A平移到B(4,b)，点B在直线AM上，
∴b=12×4+2=4，
∴B4,4，
∵四边形ADEB是菱形，
∴ AD=AB=4+22+4−12 =35，
设Dn,−14n2−n，
∴AD=n+22+−14n2−n−12，
∴n+22+−14n2−n−12=35，
整理得：n+24+16n+22−720=0，
解得：n+22=20，n+22=−36（舍去），
∴n1=25−2，n2=−25−2，
当n1=25−2时，
y=−14×25−22−25−2 =−4，
当n2=−25−2时，
y=−14−25−22−−25−2 =−4，
∴D点坐标25−2,4或−25−2,4．
【点睛】本题考查了待定系数法，解直角三角形，二次函数与特殊三角形综合，二次函数与特殊四边形综合，垂线段最短等，能将最值转化为垂线段最短，并将动点问题转化成方程求解是解题的关键．
5．（2024·山西大同·一模）综合与探究
如图，抛物线y=12x2−2x−6与x轴交于点A和B，点A在点B的左侧，交y轴于点C，作直线BC．
(1)求点B的坐标及直线BC的表达式；
(2)当点D在直线BC下方的抛物线上运动时，连接OD交BC于点E，若DEOE=512，求点D的坐标；
(3)抛物线上是否存在点F．使得∠BCF=15°?若存在，直接写出点F的坐标；若不存在，请说明理由．
【答案】(1)点B的坐标是6,0，直线BC的表达式是y=x−6；
(2)点D的坐标是1,−152或5,−72；
(3)存在，点F的坐标是4+23,43或12+233,43−163．
【分析】
（1）令y=0和x=0，解方程即可求得点B和点C的坐标，再利用待定系数法即可求解；
（2）作DH⊥x轴，垂足为H，交直线BC于点G，证明△DGE∽△OCE，利用相似三角形的性质求解即可；
（3）分两种情况讨论，利用待定系数法和解方程组即可求解．
【详解】（1）解：令y=0，解方程12x2−2x−6=0得x=−2或x=6，
∴点B的坐标为6，0；
令x=0，则y=−6，
∴点C的坐标为0，−6；
设直线BC的表达式为y=kx−6，则0=6k−6，
解得k=1，
∴直线BC的表达式为y=x−6；
（2）解：作DH⊥x轴，垂足为H，交直线BC于点G，
∴DG∥OC，
∵点C的坐标为0，−6，
∴OC=6，
设点D的坐标为m，12m2−2m−6，则点G的坐标为m，m−6，
∴GD=m−6−12m2+2m+6=−12m2+3m，
∵DG∥OC，
∴△DGE∽△OCE，
∴DGOC=DEOE，
∴−12m2+3m6=512，整理得m2−6m+5=0，
解得m=5或m=1，
∴点D的坐标为1,−152或5,−72；
（3）解：∵点B的坐标为6，0，点C的坐标为0，−6，
∴OB=OC=6，
∴△OBC是等腰直角三角形，
∴∠OCB=45°，
∵∠BCF=15°，
∴∠OCF=60°或∠OCF=30°，
当∠OCF=60°时，以OC为边作等边△OCM，直线CM交抛物线于点F，此时∠BCF=15°，如图，
作MN⊥y轴于点N，
在Rt△OMN中，OM=OC=6，ON=12OC=3，
∴MN=OM2−ON2=33，
∴点M的坐标为33，−3，同理，求得直线MC的表达式为y=33x−6，联立y=33x−6y=12x2−2x−6，
解得x=12+233y=43−163或x=0y=−6（舍去），
∴点F的坐标是12+233,43−163；
当∠OCF=30°时，设CF交x轴于点K，此时∠BCF=15°，如图，
在Rt△OCK中，OC=6，∠OCK=30°，
∴OK=OC⋅tan30°=23，
∴点K的坐标为23，0，
同理，求得直线CK的表达式为y=3x−6，
联立y=3x−6y=12x2−2x−6，
解得x=4+23y=43或x=0y=−6（舍去），
∴点F的坐标是4+23,43；
综上，点F的坐标是4+23,43或12+233,43−163．
【点睛】本题考查了一次函数表达式的确定，函数图象上点的坐标特征，二次函数图象和性质，解一元二次方程，相似三角形的判定和性质，勾股定理，分类讨论思想等，属于中考压轴题，解题关键是熟练掌握待定系数法，运用方程思想和分类讨论思想．
6．（2024·安徽合肥·一模）如图，抛物线y=−x2+bx+c过点−2,−5和2,3．

(1)求抛物线的函数表达式；
(2)已知该抛物线与x轴交于点A，B（点A位于点B的左侧），与y轴交于点C．
①若点P是该抛物线位于第一象限部分上的一动点，过点P作x轴的垂线交BC于点Q，求PQ的最大值及此时点P的坐标；
②若点M是抛物线对称轴上一动点，是否存在以点B，C，M为顶点的三角形是直角三角形？若存在，请在备用图上画出符合条件的图形，并求出点M的坐标；若不存在，请说明理由．
【答案】(1)y=−x2+2x+3
(2)①最大值为94，点P坐标为32,154；
②点M的坐标为1,−2或1,4或1,3+172或1,3−172
【分析】
（1）将点−2,−5和2,3代入y=−x2+bx+c，得到方程组，解方程组即可．
（2）①设点Pa,−a2+2a+3，求出直线BC表达式y=−x+3，则Qa,−a+3，再用a的代数式表达出PQ，最后转化为二次函数求最值即可；
②设点M的坐标为1,m，而点B、C坐标已知，用两点之间距离公式求出BC以及表示出BM、CM，分类三种情况讨论，由勾股定理建立方程，解方程即可．
【详解】（1）解：∵抛物线y=−x2+bx+c过点−2,−5和2,3，
∴−4−2b+c=−5−4+2b+c=3，解得b=2c=3，
∴抛物线的函数表达式为y=−x2+2x+3．
（2）解：当x=0时，y=3，∴点C的坐标为0,3；
当y=0时，−x2+2x+3=0，解得x=3或x=−1，
∵点A位于点B的左侧，∴点A的坐标为−1,0，点B的坐标为3,0．
①设点P的横坐标为a0设直线BC的函数表达式为y=kx+n，
根据题意得n=33k+n=0，解得k=−1n=3，
∴直线BC的函数表达式为y=−x+3，∴点Q的纵坐标为−a+3，∴PQ=−a2+2a+3−(−a+3)=−a2+3a=−a−322+94，
∵−1<0，∴此抛物线的开口向下，
∵0②存在以点B，C，M为顶点的三角形是直角三角形．
∵抛物线y=−x2+2x+3的对称轴为直线x=−22×(−1)=1，∴设点M的坐标为1,m．
分两种情况：i）以BC为直角边，如图，则BC2+CM12=BM12或BC2+BM22=CM22，
∴18+1+m−32=4+m2或18+4+m2=1+m−32，解得m=4或m=−2，
∴点M1的坐标为1,4，点M2的坐标为1,−2；
ii）以BC为斜边，如图，则BC2=CM2+BM2，∴18=1+m−32+4+m2，整理得m2−3m−2=0，解得m=3±172，∴点M3的坐标为1,3+172，点M4的坐标为1,3−172，
综上，点M的坐标为1,−2或1,4或1,3+172或1,3−172．

【点睛】本题是二次函数综合题，主要考查了待定系数法求函数解析式，配方法求最值，勾股定理的运用，其中直角三角形的存在性问题和分类讨论的思想是函数综合题常考题型．
7．（2024·安徽阜阳·一模）如图，抛物线y=ax2+bx+3与x轴交于A−1，0，B3，0两点，与y轴交于点C．
(1)求抛物线的解析式；
(2)在抛物线的对称轴上找一点 P，使△PAC的周长最小，求△PAC的周长的最小值及此时点P的坐标；
(3)若M为抛物线在第一象限内的一动点，求出四边形OCMB的面积的最大值及此时点M的坐标.
【答案】(1)y=−x2+2x+3；
(2)△PAC的周长的最小值为10+32，点P的坐标为1，2；
(3)S四边形OCMB的最大值为638，此时M32，154．
【分析】
题目主要考查二次函数的综合问题，包括待定系数法确定函数解析式，最短周长及最大面积问题，理解题意，熟练掌握二次函数的应用是解题关键．
（1）利用待定系数法求解即可；
（2）连接BC交对称轴于点P，此时△PAC的周长最小，利用勾股定理以及待定系数法求得直线BC的解析式，据此求解即可；
（3）连接OM，设Mm，−m2+2m+3，根据S四边形OCMB=12OB⋅yM+12OC⋅xM列得二次函数的解析式，利用二次函数的性质求解即可．
【详解】（1）解：由题意得a−b+3=09a+3b+3=0，
解得a=−1b=2，
∴抛物线的解析式为y=−x2+2x+3；
（2）解：∵y=−x−12+4，
∴抛物线的对称轴为直线x=1，
连接BC交对称轴于点P，此时，PA+PC取得最小值，最小值为PB的长，
令x=0，则y=3，
∴C0，3，
∵A−1，0，B3，0，
∴AC=12+32=10，BC=32+32=32，
∴△PAC的周长的最小值为AC+PA+PC=AC+BC=10+32，
设直线BC的解析式为y=kx+3，
则0=3k+3，
解得k=−1,
∴直线BC的解析式为y=−x+3，
当x=1时，y=−1+3=2，
∴点P的坐标为1，2；
（3）解：连接OM，设Mm，−m2+2m+3，
依题意得S四边形OCMB=12OB⋅yM+12OC⋅xM
=32−m2+2m+3+32m
=−32m2−3m−3
=−32m−322+638，
∵−32<0，
∴当m=32时，S四边形OCMB有最大值，最大值为638，此时M32，154．
8．（2024·陕西西安·二模）如图，在平面直角坐标系中，抛物线y=ax2+bx+2(a≠0)与x轴分别交于A，B两点，点A的坐标是(−4,0)，点B的坐标是(1,0)，与y轴交于点C，P是抛物线上一动点，且位于第二象限，过点P作PD⊥x轴，垂足为D，线段PD与直线AC相交于点E

(1)求该抛物线的解析式；
(2)连接OP，是否存在点P，使得∠OPD=2∠CAO？若存在，求出点P的横坐标；若不存在，请说明理由．
【答案】(1)抛物线的解析式为y=−12x2−32x+2；
(2)点P的横坐标为−3−734．
【分析】本题考查二次函数的综合应用，涉及待定系数法，锐角三角函数等知识，解题的关键是用含字母的代数式表示相关点坐标和相关线段的长度．
（1）由待定系数法即可求解；
（2）证明∠H=∠CAO，则tanH=tan∠CAO，由PH=OP，即可求解．
【详解】（1）解：设抛物线的表达式为：y=a(x+4)(x−1)=a(x2+3x−4)，
则−4a=2，
解得：a=−12，
∴抛物线的解析式为y=−12x2−32x+2；
（2）解：设存在点P，使得∠OPD=2∠CAO，理由如下：
延长DP到H，设PH=OP，连接OH，如图：

∵PH=OP，
∴∠H=∠POH，
∴∠OPD=∠H+∠POH=2∠H，
∵∠OPD=2∠CAO，
∴∠H=∠CAO，
∴tanH=tan∠CAO，
∴ ODDH=COOA=24=12，
∴DH=2OD，
设Pt,−12t2−32t+2，则OD=−t，PD=−12t2−32t+2，
∴DH=2OD=−2t，
∴PH=DH−PD=−2t−−12t2−32t+2=12t2−12t−2，
∵PH=OP，
∴ 12t2−12t−2=t2+12t2+32t−22，
∴t2+t−4−2t=t2，
解得t=0（舍去）或−3+734（舍去）或−3−734，
∴点P的横坐标为−3−734．
9．（2024·山东淄博·一模）如图，抛物线y=12x2＋bx＋c与y轴交于点C0,−4，与x轴交于点A，B，且B点的坐标为2,0．
(1)求该抛物线的解析式．
(2)若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．
(3)若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．
【答案】(1)y=12x2+x−4
(2)3
(3)−2，−2或−1，−3
【分析】（1）利用待定系数法求出抛物线的解析式；
（2）首先求出△PCE面积的表达式，然后利用二次函数的性质求出其最大值；
（3）△OMD为等腰三角形，可能有三种情形，需要分类讨论．
【详解】（1）解：把点C0,−4，B2,0分别代入y=12x2＋bx＋c中，
得c=−412×22+2b+c=0，
解得b=1c=−4，
∴该抛物线的解析式为y=12x2+x−4．
（2）解：令y=0，即12x2+x−4=0，
解得x1=−4，x2=2，
∴A−4，0，
∵C0,−4，B2,0，
∴AB=2−−4=6，OC=4，
∴S△ABC=12AB⋅OC=12．
设P点坐标为x,0，则PB=2−x，

∵PE∥AC，
∴∠BPE=∠BAC，∠BEP=∠BCA，
∴△PBE∽△ABC，
∴S△PBES△ABC=PBAB2，即S△PBE12=2−x62，
化简得：S△PBE=132−x2，
∴S△PCE=S△PCB−S△PBE
=12PB⋅OC−S△PBE
=12×2−x×4−132−x2
=−13x2−23x+83
=−13x+12+3，
∴当x=−1时，S△PCE的最大值为3．
（3）解：△OMD为等腰三角形，可能有三种情形：
①当DM=DO时，如图①所示．
则DO=DM=DA=2，
∵AO=CO=4，∠AOC=90°，
∴∠OAC=∠AMD=45°，
∴∠ADM=90°，
∴M点的坐标为−2，−2；
②当MD=MO时，如图②所示．
过点M作MN⊥OD于点N，则点N为OD的中点，
∴DN=ON=1，AN=AD+DN=3，
又△AMN为等腰直角三角形，
∴MN=AN=3，
∴M点的坐标为−1，−3；
③当OD=OM时，
∵△OAC为等腰直角三角形，
∴点O到AC的距离为22×4=22，即AC上的点与点O之间的最小距离为22．
∵22>2，
∴OD=OM的情况不存在．
综上所述，点M的坐标为−2，−2或−1，−3．
【点睛】本题是二次函数综合题，考查了二次函数的图象与性质、待定系数法、相似三角形、等腰三角形等知识点，以及分类讨论的数学思想．第（2）问将面积的最值转化为二次函数的最值问题，注意其中求面积表达式的方法；第（3）问重在考查分类讨论的数学思想，注意三种可能的情形需要一一分析，不能遗漏．
考点要求
命题预测
二次函数与几何压轴
二次函数的压轴题主要考向：
1）存在性问题（全等与相似、特殊三角形（直角、等腰、等边）、平行四边形（含特殊平行四边形）等）．
2）最值问题（线段、周长、面积）
常见有关二次函数的题型和应对策略：
1）线段最值（周长）问题——斜化直策略
2）三角形或多边形面积问题——铅垂高、水平宽策略
3）线段和最小值问题——将军饮马、阿氏圆模型
4）线段差——三角形三边关系或函数
5）相似三角形存在性问题——根据相等角分类讨论
6）平行四边形存在性问题——中点公式＋平移法
问题
分情况
找点
画图
解法
已知点A，B和直线l，在l上求点P，使△PAB为等腰三角形
以AB为腰
分别以点A，B为圆心，以AB长为半径画圆，与已知直线的交点P1，P2，P3，P4即为所求
分别表示出点A，B，P的坐标，再表示出线段AB，BP，AP的长度，由①AB＝AP；②AB＝BP；③BP＝AP列方程解出坐标
以AB为底
作线段AB的垂直平分线，与已知直线的交点P5即为所求
问题
分情况
找点
画图
解法
已知点A，B和直线l，在l上求点P，使△PAB为直角三角形
以AB为直角边
分别过点A，B作AB的垂线，与已知直线的交点P1，P4即为所求
分别表示出点A，B，P的坐标，再表示出线段AB，BP，AP的长度，由①AB2＝BP2＋AP2；②BP2＝AB2＋AP2；③AP2＝AB2＋BP2列方程解出坐标
以AB为斜边
以AB的中点Q为圆心，QA为半径作圆，与已知直线的交点P2，P3即为所求