北师大版九年级上册4 探索三角形相似的条件教课ppt课件

这是一份北师大版九年级上册4 探索三角形相似的条件教课ppt课件，共15页。PPT课件主要包含了成比例等内容，欢迎下载使用。

1. 相似三角形的判定定理2： 两边 且夹角 的两个三角形相似.2. 相似三角形的判定定理3： 三边 的两个三角形相似.
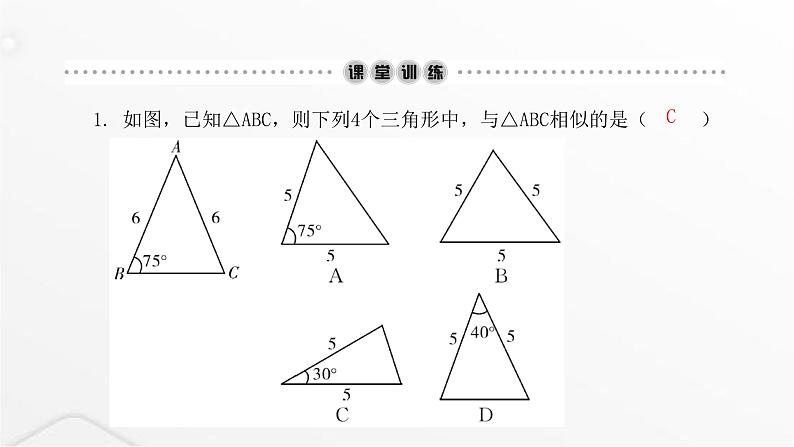
1. 如图，已知△ABC，则下列4个三角形中，与△ABC相似的是（）
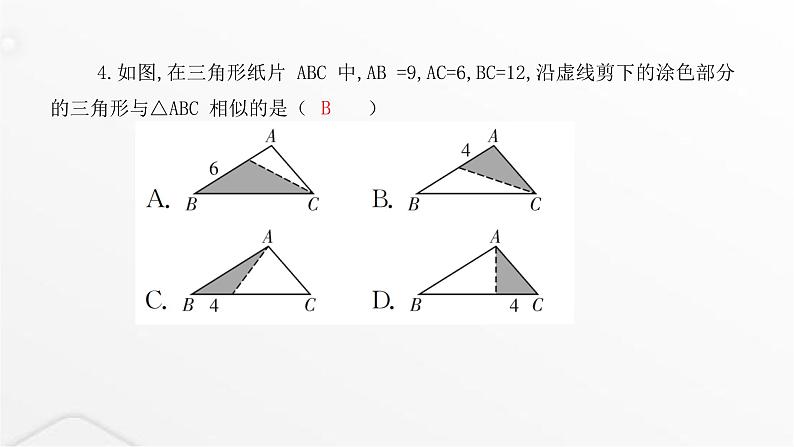
4.如图,在三角形纸片 ABC 中,AB =9,AC=6,BC=12,沿虚线剪下的涂色部分的三角形与△ABC 相似的是（ ）
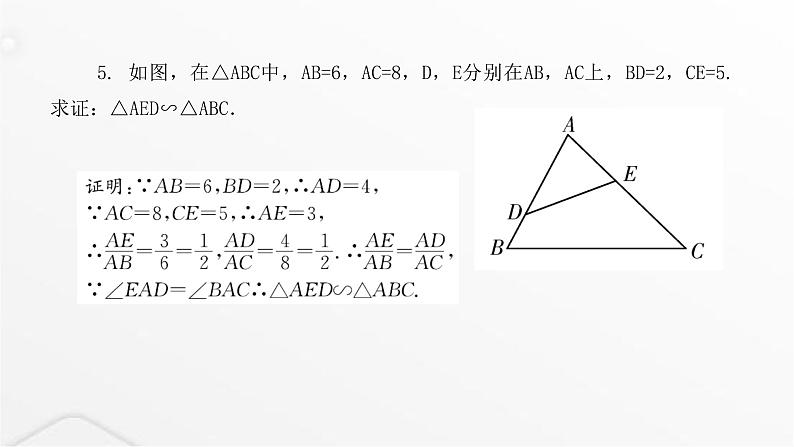
5. 如图，在△ABC中，AB=6，AC=8，D，E分别在AB，AC上，BD=2，CE=5.求证：△AED∽△ABC．
3. 如图，E是ABCD的边BC延长线上一点，连接AE交CD于点F，则图中的相似三角形共有( )A. 1对B. 2对C. 3对D. 4对
4. 如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ABC相似的是()5. 如图，在△ABC中，∠B=25°，AD是边BC上的高且AD²=BD·DC，则∠BCA的度数为 .
【提升训练】6. 如图，在△ABC中，P为AB上一点，下列四个条件：①∠ACP＝∠B；②∠APC＝∠ACB；③AC2＝AP·AB；④AB·CP＝AP·CB.其中能满足△APC与△ACB相似的条件是()A. ①②③B. ①③④C. ②③④D. ①②④
7. 如图，在正方形ABCD中，E是AD的中点，点F在CD上，且CD=4DF，连接EF,BE.求证：△ABE∽△DEF．
8. 如图，在Rt△ABC中，已知∠BAC=90°，AB=AC=2，点D在BC上运动（不能到达点B，C），过点D作∠ADE=45°，ED交AC于点E.（1）求证：△ABD∽△DCE；（2）当△ADE是等腰三角形时，求AE的长.
（1）证明：在Rt△ABC中，∠BAC=90°，AB=AC=2,∴∠B=∠C=45°,∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,∴∠ADE+∠EDC=∠B+∠BAD.又∠ADE=45°=∠B，∴∠EDC=∠BAD,∴△ABD∽△DCE,
【拓展训练】9. 如图，在△ABC中，∠BAC=90°，AD是边BC上的高，E是边BC上的一个动点（不与点B，C重合），EF⊥AB，EG⊥AC，垂足分别为F，G.（1）试说明等式EGAD=CGCD成立；（2）FD与DG垂直吗？请说明理由.（3）当AB=AC时，△FDG是等腰直角三角形吗？请说明理由.