


【专项复习】高考数学专题04 回归直线方程与非线性回归方程 (题型训练).zip
展开一、必备秘籍
1.两个变量线性相关
(1)散点图:将样本中个数据点(i=1,2,…,)描在平面直角坐标系中得到的图形.
(2)正相关与负相关
①正相关:散点图中的点散布在从左下角到右上角的区域.
②负相关:散点图中的点散布在从左上角到右下角的区域.
2.回归直线的方程
(1)回归直线:如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
(2)回归方程:回归直线对应的方程叫回归直线的方程,简称回归方程.
(3)回归方程的推导过程:
①假设已经得到两个具有线性相关关系的变量的一组数据,,.
②设所求回归方程为,其中是待定参数.
③由最小二乘法得
其中,是回归方程的斜率,是截距.
3、换元法求非线性回归方程
当经验回归方程并非形如()时,称之为非线性经验回归方程,当两个变量不呈线性相关关系时,依据样本点的分布选择合适的曲线方程来模拟,常见的非线性经验回归方程的转换方式总结如下:
4、建立非线性经验回归模型的基本步骤
(1)确定研究对象,明确哪个是解释变量,哪个是响应变量;
(2)由经验确定非线性经验回归方程的模型;
(3)通过变换(一般题目都有明显的暗示如何换元,换元成什么变量),将非线性经验回归模型转化为线性经验回归模型(特别注意:使用线性回归方程的公式,注意代入变换后的变量);
(4)按照公式计算经验回归方程中的参数,得到经验回归方程;
(5)消去新元,得到非线性经验回归方程;
(6)得出结果后分析残差图是否有异常 .
二、典型题型
题型一:线性回归
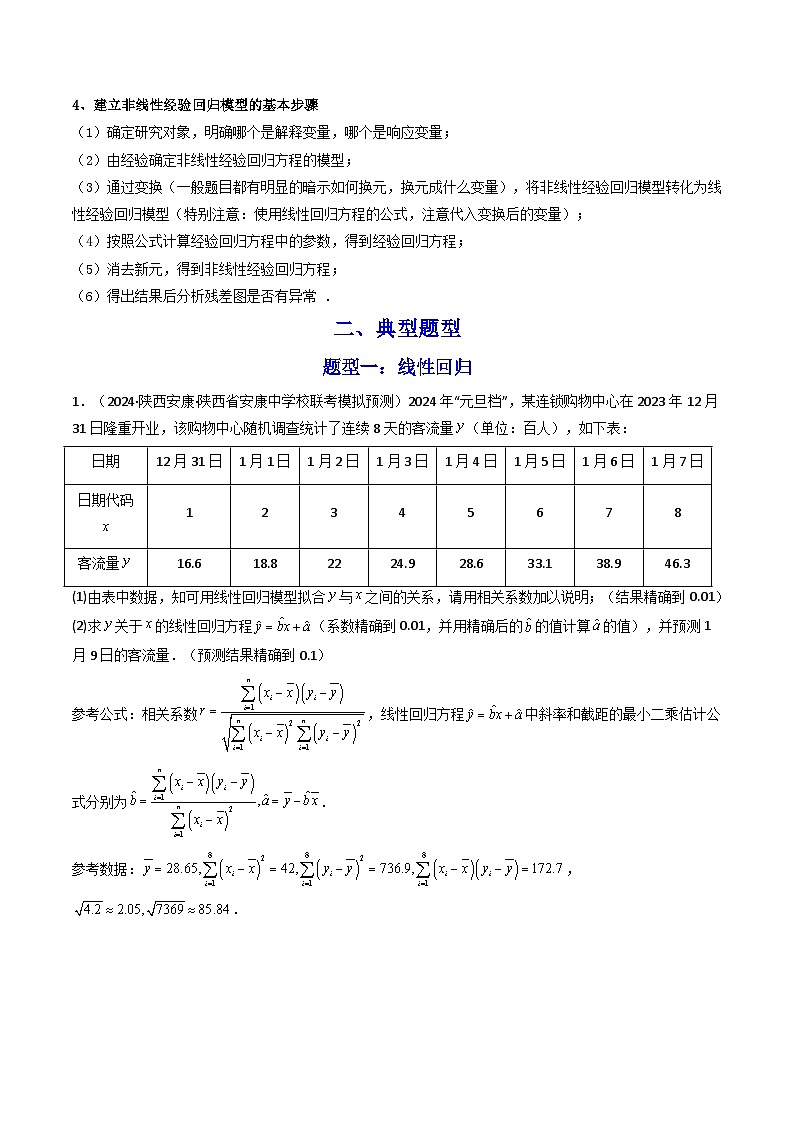
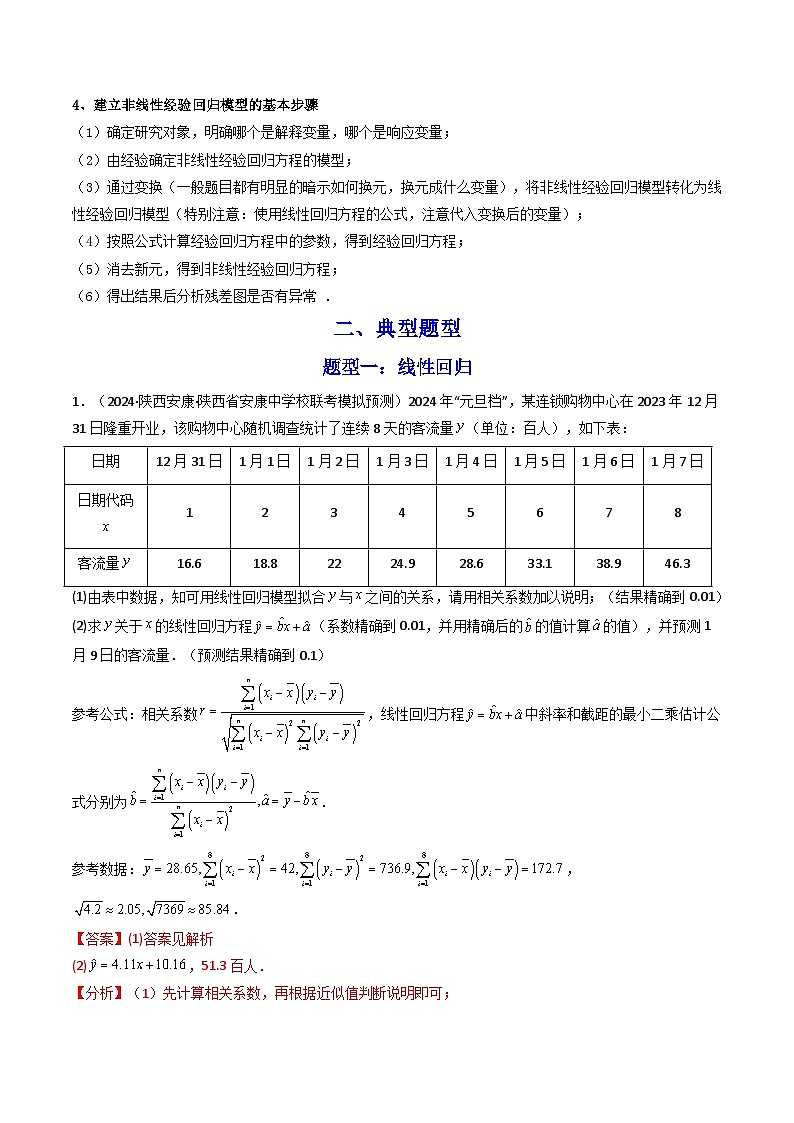
1.(2024·陕西安康·陕西省安康中学校联考模拟预测)2024年“元旦档”,某连锁购物中心在2023年12月31日隆重开业,该购物中心随机调查统计了连续8天的客流量(单位:百人),如下表:
(1)由表中数据,知可用线性回归模型拟合与之间的关系,请用相关系数加以说明;(结果精确到0.01)
(2)求关于的线性回归方程(系数精确到0.01,并用精确后的的值计算的值),并预测1月9日的客流量.(预测结果精确到0.1)
参考公式:相关系数,线性回归方程中斜率和截距的最小二乘估计公式分别为.
参考数据:,.
【答案】(1)答案见解析
(2),51.3百人.
【分析】(1)先计算相关系数,再根据近似值判断说明即可;
(2)先根据公式计算得出回归直线,再根据回归直线预测即得.
【详解】(1)由题意,知,
所以相关系数.
因为与的相关系数,接近于1,
所以与的线性相关程度很高,可用线性回归模型拟合与之间的关系.
(2)因为,
,所以关于的线性回归方程为.
又1月9日对应的日期代码,
当时,,所以预测1月9日的客流量约为51.3百人.
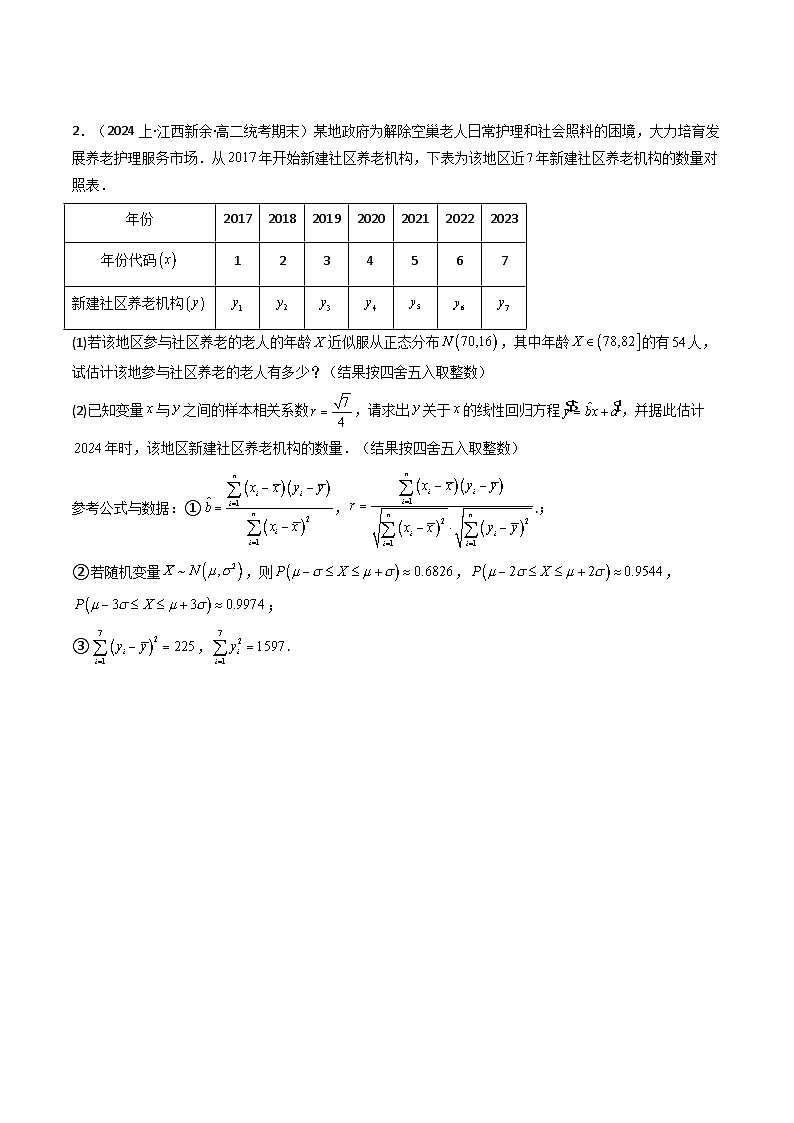
2.(2024上·江西新余·高二统考期末)某地政府为解除空巢老人日常护理和社会照料的困境,大力培育发展养老护理服务市场.从年开始新建社区养老机构,下表为该地区近年新建社区养老机构的数量对照表.
(1)若该地区参与社区养老的老人的年龄近似服从正态分布,其中年龄的有人,试估计该地参与社区养老的老人有多少?(结果按四舍五入取整数)
(2)已知变量与之间的样本相关系数,请求出关于的线性回归方程,并据此估计年时,该地区新建社区养老机构的数量.(结果按四舍五入取整数)
参考公式与数据:①,.;
②若随机变量,则,,;
③,.
【答案】(1)约为人
(2)回归方程为;约为个.
【分析】(1)利用原则求出的值,即可求得该地参与社区养老的老人人数为;
(2)计算出的值,可求出的值,可求得的值,利用参考数据可求得的值,由此可得出回归直线方程,然后将代入回归直线方程可得结果.
【详解】(1)解:由题意可知,,,则,,
所以,
,
所以,估计该地参与社区养老的老人人数为.
(2)解:由表格中的数据可得,
所以,,
由已知条件可得,
所以,,
所以,,
又因为,
显然,解得,则,
所以,关于的回归直线方程为,
当时,.
估计年时,该地区新建社区养老机构的数量约为个.
3.(2023上·江苏扬州·高三统考阶段练习)随着时代的不断发展,社会对高素质人才的需求不断扩大,我国本科毕业生中考研人数也不断攀升,年的考研人数是万人,年考研人数是万人.某省统计了该省其中四所大学年的毕业生人数及考研人数(单位:千人),得到如下表格:
(1)已知与具有较强的线性相关关系,求关于的线性回归方程;
(2)假设该省对选择考研的大学生每人发放万元的补贴.
(i)若该省大学年毕业生人数为千人,估计该省要发放多少万元的补贴?
(ii)若A大学的毕业生中小江、小沈选择考研的概率分别为p、2p-1,该省对小江、小沈两人的考研补贴总金额的期望不超过万元,求p的取值范围.
参考公式:,.
【答案】(1)
(2)(i)5028万元(ii)
【分析】(1)利用题中的数据代入参考公式,即求出线性回归方程;
(2)(i)直接将将x=120代入(1)中所求的线性回归方程计算即可;
(ii)先求出小江、小沈两人中考研人数的数学期望,再求出考研补贴的总期望,根据题意列出不等式组求解p的范围.
【详解】(1)由题意得,,
又,
,
,
,
所以,
故得y关于x的线性回归方程为;
(2)(i)将x=120代入,
估计该省要发放补贴的总金额为(万元);
(ii)设小江、小沈两人中选择考研的人数为,则的所有可能值为、、,
,
,
,
,
,可得,
又因为,可得,
故.
4.(2023下·河南焦作·高二校考阶段练习)某地区实行社会主义新农村建设后,农村的经济收入明显增加,根据统计得到从2015年至2021年农村居民家庭收入y(单位:万元)的数据,其数据如下表:
附:回归直线的斜率和截距的最小二乘估计公式分别为,.
参考数据:,.
(1)求y关于t的线性回归方程;
(2)根据(1)中的回归方程,分析2015年至2021年该地区农村居民家庭收入的变化情况,并预测该地区2024年农村居民家庭收入.
【答案】(1)
(2)2015年至2021年该地区农村居民家庭收入逐年增加,每年大约增加0.5万元,该地区2024年农村居民家庭收入为8.3万元.
【分析】(1)根据表中数据,结合最小二乘法的公式,求得,即可求得回归直线方程;
(2)由(1)知,阿静代入线性回归方程,求得,即可得到结论.
【详解】(1)解:由表中数据可得,,
,
,
则,又,
故所求线性回归方程为.
(2)解:由(1)可知,,
故2015年至2021年该地区农村居民家庭收入逐年增加,每年大约增加0.5万元,
将2024年的年份代号代入(1)中的线性回归方程得,,
故预测该地区2024年农村居民家庭收入为8.3万元.
题型二:非线性回归
1.(2024下·重庆·高三重庆一中校考开学考试)当前,人工智能技术以前所未有的速度迅猛发展,并逐步影响我们的方方面面,人工智能被认为是推动未来社会发展和解决人类面临的全球性问题的重要手段.某公司在这个领域逐年加大投入,以下是近年来该公司对产品研发年投入额(单位:百万元)与其年销售量y(单位:千件)的数据统计表.
(1)公司拟分别用①和②两种方案作为年销售量关于年投入额的回归分析模型,请根据已知数据,确定方案①和②的经验回归方程;(计算过程保留到小数点后两位,最后结果保留到小数点后一位)
(2)根据下表数据,用决定系数(只需比较出大小)比较两种模型的拟合效果哪种更好,并选择拟合精度更高的模型,预测年投入额为百万元时,产品的销售量是多少?
参考公式及数据:,,,,,,,, .
【答案】(1),
(2)②的拟合效果好,预测销售量是千件
【分析】(1)根据经验回归方程的求法求得正确答案.
(2)通过计算决定系数确定拟合效果较好的方案,并由此进行预测.
【详解】(1),
所以,
所以.
由,两边取以为底的对数得,即,
,
所以,所以.
(2),
对于,;对于,,
所以②的拟合效果好,当时,预测值千件.
2.(2021上·四川成都·高三石室中学校考期末)为帮助乡村脱贫,某勘探队计划了解当地矿脉某金属的分布情况,测得了平均金属含量(单位:)与样本对原点的距离(单位:m)的数据,并作了初步处理,得到了下面的一些统计理的值.(表中,)
(1)利用样本相关系数的知识,判断与哪一个更适宜作为平均金属含量关于样本对原点的距离的回归方程类型?
(2)根据(1)的结果回答下列问题:
①建立关于的回归方程;
②样本对原点的距离时,金属含量的预报值是多少?
附:对于一组数据,其线性相关系数,其回归直线的斜率和截距的最小二乘估计分别为:,.
【答案】(1)更适宜;
(2)①;②
【分析】(1)分别求出与所对应的线性相关系数,然后比较大小即可判断.
(2)根据数据和公式即可求得关于的回归方程,根据回归方程代入,即可求出金属含量的预报值.
【详解】(1)由题的线性相关系数,
的线性相关系数,
因为,所以,
所以更适宜作为平均金属含量关于样本对原点的距离的回归方程类型.
(2)①由(1),令,,
则,
所以,,
则,
即.
②当时,
金属含量的预报值
3.(2023·全国·模拟预测)一座城市的夜间经济不仅有助于拉动本地居民内需,还能延长外地游客、商务办公者等的留存时间,带动当地经济发展,是衡量一座城市生活质量、消费水平、投资环境及文化发展活力的重要指标.数据显示,近年来中国各地政府对夜间经济的扶持力度加大,夜间经济的市场发展规模保持稳定增长,下表为2017—2022年中国夜间经济的市场发展规模(单位:万亿元),设2017—2022年对应的年份代码依次为1~6.
(1)已知可用函数模型拟合y与x的关系,请建立y关于x的回归方程(a,b的值精确到0.01);
(2)某传媒公司发布的2023年中国夜间经济城市发展指数排行榜前10名中,吸引力超过90分的有4个,从这10个城市中随机抽取5个,记吸引力超过90分的城市数量为X,求X的分布列与数学期望.
参考数据:
其中.
参考公式:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘法估计分别为,.
【答案】(1)
(2)分布列见解析,2
【分析】(1)将的等号两边同时取对数,再结合回归直线的斜率和截距的最小二乘法求得结果;
(2)X的所有可能取值为0,1,2,3,4,根据超几何分布求出分布列以及数学期望.
【详解】(1)将的等号两边同时取对数得,
所以.,
.
所以,
.
所以,即,
所以.
(2)由题可知X的所有可能取值为0,1,2,3,4,
,,
,,.
所以X的分布列为
.
4.(2023上·湖南衡阳·高三衡阳市八中校联考阶段练习)为了加快实现我国高水平科技自立自强,某科技公司逐年加大高科技研发投入.下图1是该公司2013年至2022年的年份代码x和年研发投入y(单位:亿元)的散点图,其中年份代码1∼10分别对应年份2013∼2022.
根据散点图,分别用模型①,②作为年研发投入y(单位:亿元)关于年份代码x的经验回归方程模型,并进行残差分析,得到图2所示的残差图.结合数据,计算得到如下表所示的一些统计量的值:
表中,.
(1)根据残差图,判断模型①和模型②哪一个更适宜作为年研发投入y(单位:亿元)关于年份代码x的经验回归方程模型?并说明理由;
(2)(i)根据(1)中所选模型,求出y关于x的经验回归方程;
(ii)设该科技公司的年利润(单位:亿元)和年研发投入y(单位:亿元)满足(且),问该科技公司哪一年的年利润最大?
附:对于一组数据,,…,,其经验回归直线的斜率和截距的最小二乘估计分别为,.
【答案】(1)选择模型②更适宜,理由见解析
(2)(i);(ii)该公司2028年的年利润最大
【分析】(1)根据残差图确定;
(2)根据最小二乘法求非线性回归方程即可求解;
【详解】(1)根据图2可知,模型①的残差波动性很大,说明拟合关系较差;
模型②的残差波动性很小,基本分布在0的附近,说明拟合关系很好,所以选择模型②更适宜.
(2)(i)设,所以,
所以,,
所以关于的经验回归方程为
(ii)由题设可得,
当取对称轴即,即时,年利润L有最大值,
故该公司2028年的年利润最大.
5.(2023·全国·模拟预测)一座城市的夜间经济不仅有助于拉动本地居民内需,还能延长外地游客、商务办公者等的留存时间,带动当地经济发展,是衡量一座城市生活质量、消费水平、投资环境及文化发展活力的重要指标.数据显示,近年来中国各地政府对夜间经济的扶持力度加大,夜间经济的市场发展规模保持稳定增长,下表为2017—2022年中国夜间经济的市场发展规模(单位:万亿元),其中2017—2022年对应的年份代码依次为1~6.
(1)已知可用函数模型拟合与的关系,请建立关于的回归方程(的值精确到0.01);
(2)某传媒公司预测2023年中国夜间经济的市场规模将达到48.1万亿元,现用(1)中求得的回归方程预测2023年中国夜间经济的市场规模,若两个预测规模误差不超过1万亿元,则认为(1)中求得的回归方程是理想的,否则是不理想的,判断(1)中求得的回归方程是否理想.参考数据:
其中.
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为.
【答案】(1);
(2)是理想的
【分析】(1)通过对所给的的函数模型取对数,转换为求回归直线方程即可,再结合题中所给的直线方程与数据即可得解.
(2)利用(1)中求得的函数模型进行预测,结合回归方程理想的定义判断即可.
【详解】(1)将的等号左右两边同时取自然对数得,
所以.,
而,
所以,
.
所以,即,
所以.
(2)2023年对应的年份代码为7,
当时,,,
所以(1)中求得的回归方程是理想的.
三、专项训练
1.(2023上·广东广州·高三广东广雅中学校考阶段练习)新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.某中医药企业根据市场调研与模拟,得到研发投入(亿元)与产品收益(亿元)的数据统计如下:
(1)计算,的相关系数,并判断是否可以认为研发投入与产品收益具有较高的线性相关程度?(若,则线性相关程度一般,若,则线性相关程度较高)
(2)求出关于的线性回归方程,并预测若想收益超过50(亿元)则需研发投入至少多少亿元?(结果保留一位小数)参考数据:,.
附:相关系数公式:,
回归直线方程的斜率,截距.
【答案】(1),线性相关程度较高
(2)回归直线方程为;至少投资亿元
【分析】(1)通过计算相关系数来进行判断.
(2)先计算回归直线方程,并由此作出预测.
【详解】(1),
,
,,
所以,所以线性相关程度较高.
(2)由(1)得,,
所以,,
所以,由,
得,所以至少投资亿元.
2.(2023上·辽宁丹东·高三统考期中)哈尔滨冰雪大世界于2022年9月投入使用,总投资高达25亿元,号称“永不落幕”的冰雪游乐场,从“一季繁荣”到“四季绽放”2023年1月至5月的游客数以及对游客填写满意与否的调查表,统计如下:
已知关于的线性回归直线方程为.
(1)求2月份,3月份的游客数的值;
(2)在1月至5月的游客中随机抽取2人进行调查,把满意率视为概率,求评价为满意的人数的分布列与期望.
(参考公式:)
【答案】(1)
(2)分布列见解析;
【分析】(1)根据题意中调查表及回归直线方程,可以分别求出的值;
(2)根据题意得满意率为概率,即可列出分布列,求解出期望.
【详解】(1)由题意可得,且,
所以得:,①
又因为:,,,
所以得:,化简得:,②
联立①②得:.
(2)任取1个人满意的概率,
所以满意的人数服从二项分布,即,
随机变量的取值分别为:0,1,2,从而得:
,
,
,
所以可得满意人数的分布列如下表所示:
所以期望.
3.(2023上·广东广州·高三执信中学校考阶段练习)中国茶文化博大精深,饮茶深受大众喜爱,茶水的口感与茶叶类型和水的温度有关,某数学建模小组为了获得茶水温度y(单位:)关于时间x(单位:min)的回归方程模型,通过实验收集在室温,用同一温度的水冲泡的条件下,茶水温度随时间变化的7组数据,并对数据做初步处理得到如图所示散点图以及如表所示数据.
表中:,
(1)根据散点图判断,①与②哪一个更适宜作为该茶水温度y关于时间x的回归方程类型?(给出判断即可,不必说明理由)请根据你的判断结果及表中数据建立该茶水温度y关于时间x的回归方程;
(2)已知该茶水温度降至口感最佳,根据(1)中的回归方程,求在相同条件下冲泡的茶水,大约需要放置多长时间才能达到最佳饮用口感?
附:(1)对于一组数据,…,,其回归直线的斜率和截距的最小二乘估计分别为,
(2)参考数据:,,,,
【答案】(1)②更适宜,;
(2)7.5min.
【分析】(1)根据散点图选择②,取对数,再利用最小二乘法公式求出回归直线方程即可.
(2)利用(1)中回归方程,列出关于的方程求解即得.
【详解】(1)由散点图知,更适宜的回归方程为②,即.
由,得,两边取自然对数,得,
令,则,
,
结合表中数据,得,
结合参考数据可得,由,得,
所以茶水温度y关于时间x的回归方程为.
(2)依题意,室温下,茶水温度降至口感最佳,
即,整理得,
于是,解得,
所以在相同条件下,刚泡好的茶水大约需要放置7.5min才能达到最佳引用口感.
4.(2023下·河北石家庄·高二石家庄市第四十一中学校考阶段练习)研究某灌溉渠道水的流速y与水深x之间的关系,测得一组数据如下:
(1)求y对x的回归直线方程:(所有数据精确到0.01)
(2)预测水深为时水的流速是多少?(精确到0.01)
参考公式:回归方程为中,
参考数据:
【答案】(1)
(2)
【分析】(1)由最小二乘法得出回归方程;
(2)由回归方程进行预测.
【详解】(1)设y对x的回归直线方程为.
.
.
即y对x的回归直线方程为
(2)当水深为时,水的流速为.
5.(2023上·黑龙江牡丹江·高三牡丹江市第三高级中学校考阶段练习)某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1)画出散点图,观察散点图,说明两个变量有怎样的相关性;
(2)用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)当销售额为4(千万元)时,估计利润额的大小.
参考公式:,,.
【答案】(1)答案见解析
(2)
(3)2.4(百万元)
【分析】(1)根据已知数据作出散点图,由图形从而得出相关性;
(2)根据公式计算出回归方程系数得回归方程;
(3)回归方程中代入计算.
【详解】(1)散点图如下图,由散点图可知,两个变量符合正相关.
(2)设回归直线方程是,
,,
所以
,
;
故利润额对销售额的回归直线方程为.
(3)当销售额为4(千万元)时,利润额为(百万元).
6.(2023上·江苏扬州·高三统考阶段练习)高邮市某中学开展劳动主题德育活动,某班统计了本班学生1至7月份的人均月劳动时间(单位:小时),并建立了人均月劳动时间(单位:小时)关于月份的线性回归方程,与的原始数据如表所示:
由于某些原因导致部分数据丢失,但已知.
(1)求,的值;
(2)如果该月人均劳动时间超过13(单位:小时),则该月份“达标”.从表格中的7组数据中随机选5组,设表示“达标”的数据组数,求的分布列和数学期望.
参考公式:在线性回归方程中,
【答案】(1);
(2)分布列见解析,数学期望为.
【分析】(1)根据已知数据,结合最小二乘法列方程求相关参数,进而确定原数据值;
(2)由题设确定随机变量的可能值并求对应概率,写出分布列,进而求期望即可.
【详解】(1),,
,则①,
而,
所以 ,整理得②,
由,则③,
由②③得,故④,
由①④得 .
(2)由题意,可能取且,,,
的分布列为
所以.
7.(2023下·江西·高三校联考阶段练习)中医药在抗击新冠肺炎疫情中,发挥了重要作用.中药可以起到改善平常上呼吸道的症状,同时可以起到抑制病毒繁殖的效果就可以达到治疗新型冠状病毒肺炎的作用.某地种植药材收到了很好的经济效益.根据资料显示,产出的药材的箱数(单位:十箱)与成本(单位:千元)的关系如下:
与可用回归方程(其中为常数,且精确到0.01)进行模拟.
(1)若农户卖出的该药材的价格为500元/箱,试预测该药材10箱的利润是多少元;(利润=售价-成本)
(2)据统计,4月份的连续20天中农户每天为甲地可配送的药材的箱数的频率分布直方图如图,用这20天的情况来估计相应的概率.
(i)通过频率分布直方图计算农户每天平均可配送的药材的箱数(同一组中的数据以这组数据所在区间中点的值作代表);
(ii)一个运输户拟购置3辆小货车专门运输农户为甲地配送的该药材,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该药材,满载发车,否则不发车.若发车,则每辆车每趟可获利400元;若未发车,则每辆车每天平均亏损200元.试计算此项业务每天的利润平均值的大小.
参考数据:设,则
参考公式:对于一组数据,其回归直线的斜率和截距的最小二
乘估计分别为,.
【答案】(1)140
(2)125;900
【分析】(1)根据公式可求得从而得到当时求得,进而求得利润;
(2)(i)利用频率分布直方图估计平均数的计算公式可求;
(ii)根据频率分布直方图,可求该农户每天可配送的该水果的箱数的概率分布表,进而求得获利的分布列,最后根据均值的计算公式求得此项业务每天的利润平均值.
【详解】(1)
所以
所以
又,所以
所以10箱药材,时,(千元),
即该水果10箱的成本为4860元,
故该水果10箱的利润为(元).
(2)(i),
所以农户每天平均可配送125箱药材.
(ii)根据频率分布直方图,可知该农户每天可配送的该水果的箱数的概率分布表为:
该运输户购3辆车时每天的利润为Y元,
则Y的可能取值为1200,600,0,其分布列为:
故此项业务每天的利润平均值为900元。
8.(2023·云南·高三云南师大附中校考阶段练习)近年来,云南省保山市龙陵县紧紧围绕打造“中国石斛之乡”的发展定位,大力发展石斛产业,该产业带动龙陵县近四分之一人口脱贫致富.2022年8月,龙陵紫皮石斛获国家地理标志运用促进工程重点项目,并被评为优秀等次.在政府的大力扶持下,龙陵紫皮石斛产量逐年增长,2017年底到2022年底龙陵县石斛产量统计如下及散点图如图.
(1)根据散点图判断,与(a,b,c,d均为常数)哪一个更适合作为龙陵县紫皮石斛产量y关于年份代码x的回归方程类型?(给出判断即可,不必说明理由)
(2)经计算得下表中数据,根据(1)中结果,求出y关于x的回归方程;
其中.
(3)龙陵县计划到2025年底实现紫皮石斛年产量达1.5万吨,根据(2)所求得的回归方程,预测该目标是否能完成?(参考数据:)
附:,.
【答案】(1)更适合
(2)
(3)可以完成
【分析】(1)根据判断即可;
(2)根据表中数据和参考数据,利用公式求解即可;
(3)根据(2)中所得的回归方程即可预测到2025年底该目标值,从而即可判断.
【详解】(1)由散点图可知,更适合作为龙陵县紫皮石斛产量y关于年份代码x的回归方程类型.
(2)对两边取自然对数,得.
令,所以.
因为,
所以.
所以,
所以.
所以龙陵县紫皮石斛产量y关于年份代码x的回归方程为.
(3)当时,,
故预测该目标可以完成.
9.(2022下·重庆沙坪坝·高二重庆八中校考期末)有一个开房门的游戏,其玩法为:
盒中先放入两把钥匙和两把钥匙,能够打开房门,不能打开房门.
每次从盒中随机取一把试开,试开后不放回钥匙.第一次打开房门后,关上门继续试开,第二次打开房门后停止抽取,称为进行了一轮游戏.
若每一轮取钥匙不超过三次,则该轮“成功”,否则为“失败”,如果某一轮“成功”,则游戏终止;若“失败”,则将所有钥匙重新放入盒中,并再放入一把钥匙,继续下一轮抽取,直至“成功”.
(1)有名爱好者独立参与这个游戏,记表示“成功”时抽取钥匙的轮次数,表示对应的人数,部分统计数据如下表:
若将作为关于的经验回归方程,估计抽取轮才“成功”的人数(人数精确到个位);
(2)由于时间关系,规定:进行游戏时,最多进行三轮,若均未“成功”也要终止游戏.求游戏要进行三轮的概率.
参考公式:最小二乘估计,.
参考数据:取,,其中,.
【答案】(1)人
(2)
【分析】(1)利用参考数据以及最小二乘法公式求出、的值,可得出经验回归方程,然后在回归方程中令,可求得结果;
(2)设事件为“第一轮成功”,事件为“第二轮成功”,则、相互独立,分析可知游戏要进行三轮,即前两轮均失败,计算出、的值,利用对立事件和独立事件的概率公式可求得所求事件的概率.
【详解】(1)解:令,设,
由条件知,,
所以,
,从而,
故所求的回归方程为.
所以,估计当时,,即抽取轮才“成功”的人数约为人.
(2)解:由条件知,游戏要进行三轮,即前两轮均失败.
设事件为“第一轮成功”,事件为“第二轮成功”,则、相互独立.
因为,,
所以,前两轮均失败的概率为.
故游戏要进行三轮的概率为.
10.(2022·四川成都·石室中学校考二模)2020年,是人类首次成功从北坡登顶珠峰60周年,也是中国首次精确测定并公布珠峰高程的45周年.华为帮助中国移动开通珠峰峰顶5G,有助于测量信号的实时开通,为珠峰高程测量提供通信保障,也验证了超高海拔地区5G信号覆盖的可能性,在持续高风速下5G信号的稳定性,在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说:“华为公司价值体系的理想是为人类服务.”有人曾问,在珠峰开通5G的意义在哪里?“我认为它是科学技术的一次珠峰登顶,告诉全世界,华为5G、中国5G的底气来自哪里.现在,5G的到来给人们的生活带来更加颠覆性的变革,某IT公司基于领先技术的支持,5G经济收入在短期内逐月攀升,该IT公司在1月份至6月份的5G经济收入y(单位:百万元)关于月份x的数据如下表所示,并根据数据绘制了如图所示的散点图.
(1)根据散点图判断,与(a,b,c,d均为常数)哪一个更适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的结果及表中的数据,求出y关于x的回归方程,并预测该公司7月份的5G经济收入.(结果保留小数点后两位)
(3)从前6个月的收入中抽取2个,记收入超过20百万元的个数为X,求X的分布列和数学期望.参考数据:
其中,设(i=1,2,3,4,5,6).
参考公式:对于一组具有线性相关关系的数据(,)(i=1,2,3,…,n),其回归直线的斜率和截距的最小二乘估计公式分别为,.
【答案】(1)更适宜
(2),65.35百万元
(3)分布列见解析,1
【分析】(1)根据散点图确定正确答案.
(2)根据非线性回归的知识求得回归方程并求得预测值.
(3)利用超几何分布的知识求得分布列并求得数学期望.
【详解】(1)根据散点图判断,更适宜作为5G经济收入y关于月份x的回归方程类型;
(2)因为,所以两边同时取常用对数,得,设,所以,因为,所以
所以.
所以,即,所以.
令,得,
故预测该公司7月份的5G经济收入大约为65.35百万元.
(3)前6个月的收入中,收入超过20百万元的有3个,所以X的取值为0,1,2,
所以X的分布列为:
所以.
11.(2023·四川绵阳·统考二模)某县依托种植特色农产品,推进产业园区建设,致富一方百姓.已知该县近年人均可支配收入如下表所示,记年为,年为,…以此类推.
(1)使用两种模型:①;②的相关指数分别约为,,请选择一个拟合效果更好的模型,并说明理由;
(2)根据(1)中选择的模型,试建立关于的回归方程.(保留位小数)
附:回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,令,.
【答案】(1)应选择
(2)
【分析】(1)根据越大,模型拟合效果越好,可确定所选模型;
(2)令,利用最小二乘法可求得,进而得到回归方程.
【详解】(1),根据统计学知识可知:越大,模型拟合效果越好,
应选择模型.
(2)令,
,,
,
又,
,,
关于的回归方程为.
12.(2023·四川广安·统考一模)某企业为改进生产,现 某产品及成本相关数据进行统计.现收集了该产品的成本费y(单位:万元/吨)及同批次产品生产数量x(单位:吨)的20组数据.现分别用两种模型①,②进行拟合,据收集到的数据,计算得到如下值:
表中,.
若用刻画回归效果,得到模型①、②的值分别为,.
(1)利用和比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求y关于x的回归方程;并求同批次产品生产数量为25(吨)时y的预报值.
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘法估计分别为,.
【答案】(1)选择模型②,理由见解析;
(2)6.
【分析】(1)根据已知,根据的意义,即可得出模型②的拟合效果好,选择模型②;
(2)与可用线性回归来拟合,有,求出系数,得到回归方程,即可得到成本费与同批次产品生产数量的回归方程为,代入,即可求出结果.
【详解】(1)应该选择模型②.
由题意可知,,则模型②中样本数据的残差平方和比模型①中样本数据的残差平方和小,即模型②拟合效果好.
(2)由已知,成本费与可用线性回归来拟合,有.
由已知可得,,
所以,
则关于的线性回归方程为.
成本费与同批次产品生产数量的回归方程为,
当(吨)时,(万元/吨).
所以,同批次产品生产数量为25(吨)时y的预报值为6万元/吨.
曲线方程
变换公式
变换后的线性关系式
日期
12月31日
1月1日
1月2日
1月3日
1月4日
1月5日
1月6日
1月7日
日期代码
1
2
3
4
5
6
7
8
客流量
16.6
18.8
22
24.9
28.6
33.1
38.9
46.3
年份
2017
2018
2019
2020
2021
2022
2023
年份代码
1
2
3
4
5
6
7
新建社区养老机构
A大学
B大学
C大学
D大学
年毕业人数(千人)
年考研人数(千人)
年份
2015
2016
2017
2018
2019
2020
2021
年份代号t
1
2
3
4
5
6
7
农村居民家庭收入y
3.9
4.3
4.6
5.4
5.8
6.2
6.9
1
2
3
4
5
6
1
1.5
3
6
12
经验回归方程
残差平方和
6
97.90
0.21
60
0.14
14.12
26.13
年份代码x
1
2
3
4
5
6
中国夜间经济的市场发展规模y/万亿元
20.5
22.9
26.4
30.9
36.4
42.4
3.366
73.282
17.25
1.16
X
0
1
2
3
4
P
75
2.25
82.5
4.5
120
28.35
年份代码
1
2
3
4
5
6
中国夜间经济的市场发展规模万亿元
20.5
22.9
26.4
30.9
36.4
42.4
3.366
73.282
17.25
1.16
2.83
研发投入(亿元)
1
2
3
4
5
产品收益(亿元)
3
7
9
10
11
月份
1
2
3
4
5
游客人数万人)
130
90
80
满意率
0.5
0.4
0.4
0.3
0.35
0
1
2
73.5
3.85
水深x/m
1.40
1.50
1.60
1.70
1.80
1.90
2.00
2.10
流速y/()
1.70
1.79
1.88
1.95
2.03
2.10
2.16
2.21
商店名称
A
B
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
月份
人均月劳动时间
1
2
3
3
4
6
7
9
6.5
7
7.5
8
8.2
0.73
7.44
0.53
0.15
箱数
1200
600
0
年份
2017
2018
2019
2020
2021
2022
年份代码x
1
2
3
4
5
6
紫皮石斛产量y(吨)
3200
3400
3600
4200
7500
9000
3.5
5150
8.46
17.5
20950
3.85
月份x
1
2
3
4
5
6
收入y(百万元)
6.6
8.6
16.1
21.6
33.0
41.0
3.50
21.15
2.85
17.70
125.35
6.73
4.57
14.30
0
1
2
P
年份
年份代号
人均可支配收入(万元)
14.5
0.08
665
0.04
-450
4
【专项复习】高考数学专题04 数列求通项(隔项等差(等比)数列)(题型训练).zip: 这是一份【专项复习】高考数学专题04 数列求通项(隔项等差(等比)数列)(题型训练).zip,文件包含专项复习高考数学专题04数列求通项隔项等差等比数列题型训练原卷版docx、专项复习高考数学专题04数列求通项隔项等差等比数列题型训练解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
【专项复习】高考数学专题04 解三角形(中线问题)(题型训练).zip: 这是一份【专项复习】高考数学专题04 解三角形(中线问题)(题型训练).zip,文件包含专项复习高考数学专题04解三角形中线问题题型训练原卷版docx、专项复习高考数学专题04解三角形中线问题题型训练解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
【专项复习】高考数学专题04 构造函数法解决不等式问题(题型训练).zip: 这是一份【专项复习】高考数学专题04 构造函数法解决不等式问题(题型训练).zip,文件包含专项复习高考数学专题04构造函数法解决不等式问题题型训练原卷版docx、专项复习高考数学专题04构造函数法解决不等式问题题型训练解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












