2023-2024学年河南省洛阳市洛龙区七年级（下）期中数学试卷（含解析）

这是一份2023-2024学年河南省洛阳市洛龙区七年级（下）期中数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）有下列命题：
①两点确定一条直线；
②相等的角是对顶角；
③内错角相等；
④邻补角是两个互补的角．
其中，假命题的个数是（ ）
A．1B．2C．3D．4
2．（3分）如图，直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝48°，则∠2等于（ ）
A．132°B．138°C．156°D．159°
3．（3分）下列图形中，∠1与∠2是同位角的有（ ）
A．②③④B．①②④C．②③D．③④
4．（3分）如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（ ）
A．互余B．相等C．互补D．不等
5．（3分）一个正数的两个不同的平方根是a+1和a﹣5，则这个正数是（ ）
A．2B．4C．9D．16
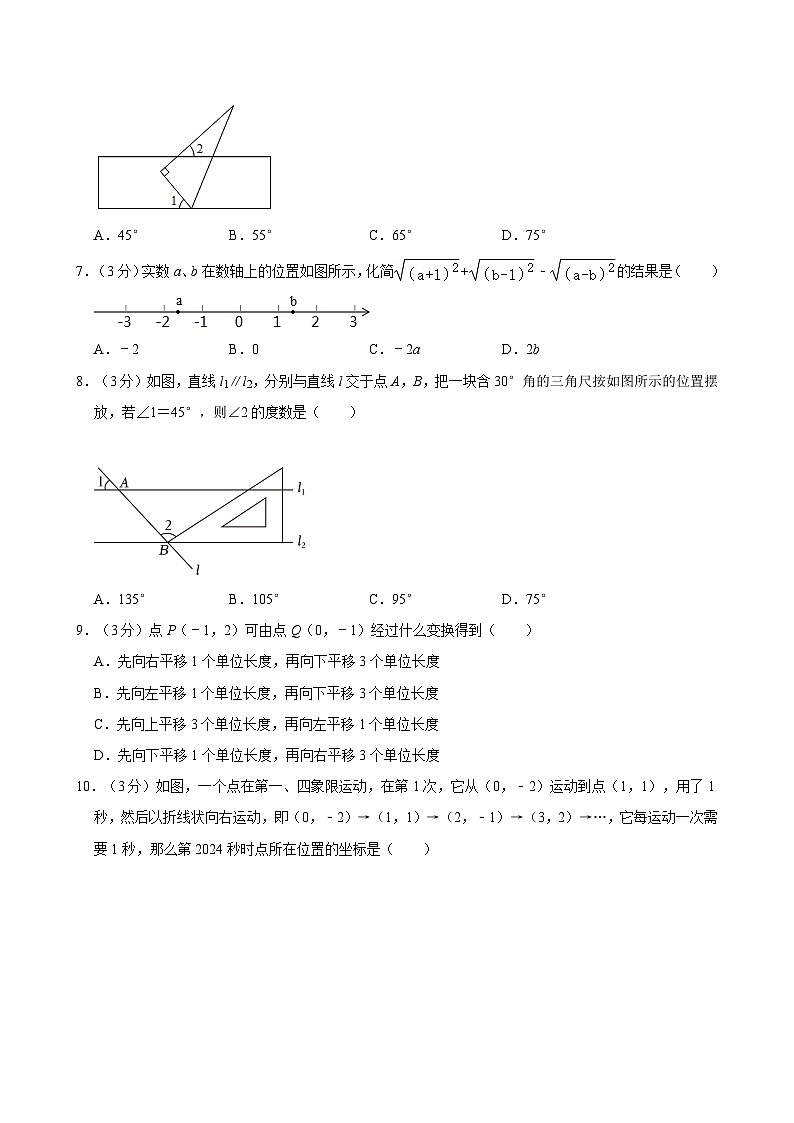
6．（3分）如图，一块直角三角尺的一个顶点落在直尺的一边上，若∠2＝35°，则∠1的度数为（ ）
A．45° B．55°C．65°D．75°
7．（3分）实数a、b在数轴上的位置如图所示，化简+﹣的结果是（ ）
A．﹣2B．0C．﹣2aD．2b
8．（3分）如图，直线l1∥l2，分别与直线l交于点A，B，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝45°，则∠2的度数是（ ）
A．135°B．105°C．95°D．75°
9．（3分）点P（﹣1，2）可由点Q（0，﹣1）经过什么变换得到（ ）
A．先向右平移1个单位长度，再向下平移3个单位长度
B．先向左平移1个单位长度，再向下平移3个单位长度
C．先向上平移3个单位长度，再向左平移1个单位长度
D．先向下平移1个单位长度，再向右平移3个单位长度
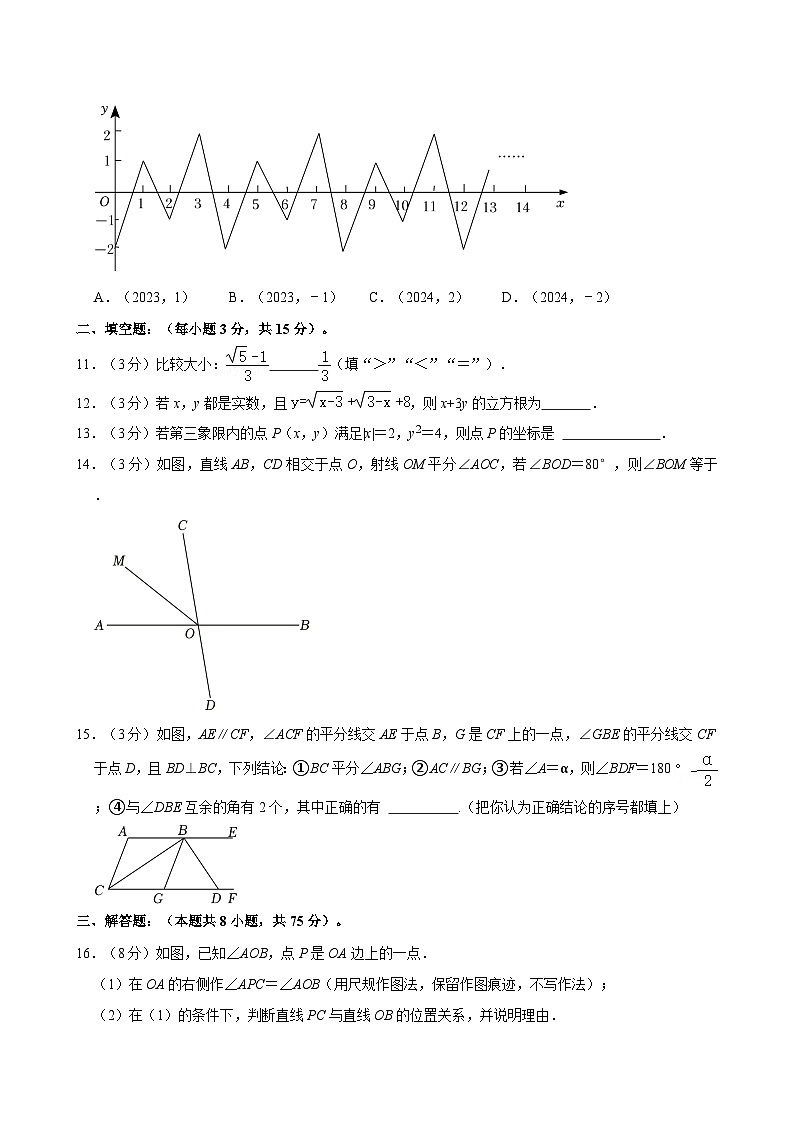
10．（3分）如图，一个点在第一、四象限运动，在第1次，它从（0，﹣2）运动到点（1，1），用了1秒，然后以折线状向右运动，即（0，﹣2）→（1，1）→（2，﹣1）→（3，2）→…，它每运动一次需要1秒，那么第2024秒时点所在位置的坐标是（ ）
A．（2023，1）B．（2023，﹣1）C．（2024，2）D．（2024，﹣2）
二、填空题：（每小题3分，共15分）。
11．（3分）比较大小： （填“＞”“＜”“＝”）．
12．（3分）若x，y都是实数，且，则x+3y的立方根为 ．
13．（3分）若第三象限内的点P（x，y）满足|x|＝2，y2＝4，则点P的坐标是 ．
14．（3分）如图，直线AB，CD相交于点O，射线OM平分∠AOC，若∠BOD＝80°，则∠BOM等于 ．
15．（3分）如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC∥BG；③若∠A＝α，则∠BDF＝180；④与∠DBE互余的角有2个，其中正确的有 .（把你认为正确结论的序号都填上）
三、解答题：（本题共8小题，共75分）。
16．（8分）如图，已知∠AOB，点P是OA边上的一点．
（1）在OA的右侧作∠APC＝∠AOB（用尺规作图法，保留作图痕迹，不写作法）；
（2）在（1）的条件下，判断直线PC与直线OB的位置关系，并说明理由．
17．（8分）计算：
（1）﹣12024﹣|﹣5|+；
（2）．
18．（10分）已知：如图所示，∠ABC＝∠ADC，BF和DE分别平分∠ABC和∠ADC，∠AED＝∠EDC．求证：ED∥BF．
证明：∵BF和DE分别平分∠ABC和∠ADC（已知）
∴∠EDC＝ ∠ADC，
∠FBA＝ ∠ABC．
又∵∠ADC＝∠ABC（已知），
∴∠ ＝∠FBA（等量代换）．
又∵∠AED＝∠EDC（已知），
∴∠ ＝∠ （等量代换），
∴ED∥BF（ ）．
19．（8分）如图所示，已知AB∥DE，∠ABC＝80°，∠CDE＝140°，求∠BCD的度数．
20．（10分）如图，直线AB和CD相交于点O，OE把∠AOC分成两部分，且∠AOE：∠EOC＝3：5，OF平分∠BOE．
（1）若∠BOD＝72°，求∠BOE．
（2）若∠BOF＝2∠AOE+15°，求∠COF．
21．（10分）在平面直角坐标系中，A，B，C三点的坐标分别为（﹣6，7）、（﹣3，0）、（0，3）．
（1）画出△ABC，并求△ABC的面积；
（2）在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出点A′，B′的坐标；
（3）P（﹣3，m）为△ABC中一点，将点P向右平移4个单位后，再向上平移6个单位得到点Q（n，﹣3），则m＝ ，n＝ ．
22．（10分）已知有理数﹣3，1．
（1）在如图所示的数轴上，标出表示这两个数的点，并分别用A，B表示．
（2）若|m|＝2，在数轴上表示数m的点介于点A，B之间；表示数n的点在点A右侧且到点B距离为6．
①计算：m＝ ，n＝
②解关于x的不等式mx+3＜n，并把解集表示在所给数轴上．
23．（11分）【阅读材料】
在“相交线与平行线”的学习中，有这样一道典型问题：
如图①，AB∥CD，点P在AB与CD之间，可得结论：∠BAP+∠APC+∠PCD＝360°．
理由如下：
过点P作PQ∥AB．
∴∠BAP+∠APQ＝180°．
∵AB∥CD，
∴PQ∥CD．
∴∠PCD+∠CPQ＝180°．
∴∠BAP+∠APC+∠PCD
＝∠BAP+∠APQ+∠CPQ+∠PCD
＝180°+180°
＝360°．
【问题解决】
（1）如图②，AB∥CD，点P在AB与CD之间，可得∠BAP，∠APC，∠PCD间的等量关系是 ；（只写结论）
（2）如图③，AB∥CD，点P，E在AB与CD之间，AE平分∠BAP，CE平分∠DCP．写出∠AEC与∠APC间的等量关系，并写出理由；
（3）如图④，AB∥CD，点P，E在AB与CD之间，∠BAE＝∠BAP，∠DCE＝∠DCP，可得∠AEC与∠APC间的等量关系是 （只写结论）
2023-2024学年河南省洛阳市洛龙区七年级（下）期中数学试卷
参考答案与试题解析
一、选择题：（每小题3分，共30分）。
1．（3分）有下列命题：
①两点确定一条直线；
②相等的角是对顶角；
③内错角相等；
④邻补角是两个互补的角．
其中，假命题的个数是（ ）
A．1B．2C．3D．4
【分析】利用确定直线的条件、对顶角的定义、平行线的性质及邻补角的定义分别判断后即可确定正确的选项．
【解答】解：①两点确定一条直线，正确，是真命题，符合题意；
②相等的角不一定是对顶角，故原命题错误，是假命题，不符合题意；
③两直线平行，内错角相等，故原命题错误，是假命题，不符合题意；
④邻补角是两个互补的角，正确，是真命题，符合题意．
真命题有2个，
故选：B．
【点评】本题考查了命题与定理的知识，解题的关键是了解有关的定义及定理，难度不大．
2．（3分）如图，直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝48°，则∠2等于（ ）
A．132°B．138°C．156°D．159°
【分析】根据平行线的性质可得∠GEB＝∠1＝48°，然后根据EF为∠GEB的平分线可得出∠FEB的度数，根据两直线平行，同旁内角互补即可得出∠2的度数．
【解答】解：∵AB∥CD，∠1＝48°，
∴∠GEB＝∠1＝48°，
∵EF为∠GEB的平分线，
∴∠FEB＝∠GEB＝24°，
∵AB∥CD，
∴∠2+∠FEB＝180°，
∴∠2＝180°﹣∠FEB＝156°．
故选：C．
【点评】本题考查了平行线的性质，解答本题的关键是掌握平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补．
3．（3分）下列图形中，∠1与∠2是同位角的有（ ）
A．②③④B．①②④C．②③D．③④
【分析】根据同位角的概念解答即可．
【解答】解：①∠1与∠2是同位角，故本选项符合题意．
②∠1与∠2是同位角，故本选项符合题意
③∠1与∠2不是同位角，故本选项不符合题意．
④∠1与∠2是同位角，故本选项符合题意．
故选：B．
【点评】此题考查的是同位角，内错角，同旁内角，掌握它们的概念是解决此题的关键．
4．（3分）如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（ ）
A．互余B．相等C．互补D．不等
【分析】根据平行线的性质得出∠CAB+∠ABD＝180°，再根据角平分线的定义得出结论．
【解答】解：∵AC∥BD，
∴∠CAB+∠ABD＝180°，
∵AO、BO分别是∠BAC、∠ABD的平分线，
∴∠CAB＝2∠OAB，∠ABD＝2∠ABO，
∴∠OAB+∠ABO＝90°，
∴∠AOB＝90°，
∴OA⊥OB，
∴∠BAO与∠ABO互余，
故选：A．
【点评】此题考查平行线的性质，关键是根据平行线的性质得出∠CAB+∠ABD＝180°．
5．（3分）一个正数的两个不同的平方根是a+1和a﹣5，则这个正数是（ ）
A．2B．4C．9D．16
【分析】根据平方根的性质求出a的值，再求出这个数即可．
【解答】解：∵这个正数的两个不同的平方根是a+1和a﹣5，
∴a+1+a﹣5＝0，
解得：a＝2，
∴a+1＝3，
∴这个正数为：32＝9，
故选：C．
【点评】本题考查平方根，解题的关键是熟练掌握平方根的性质．
6．（3分）如图，一块直角三角尺的一个顶点落在直尺的一边上，若∠2＝35°，则∠1的度数为（ ）
A．45° B．55°C．65°D．75°
【分析】根据平行线的性质和直角的定义解答即可．
【解答】解：如图，
作EF∥AB，
∵AB∥CD，
∴EF∥AB∥CD，
∴∠2＝∠AEF＝35°，∠1＝∠FEC，
∵∠AEC＝90°，
∴∠1＝90°﹣35°＝55°，
故选：B．
【点评】此题考查平行线的性质，关键是根据平行线的性质得出∠2＝∠AEF＝35°，∠1＝∠FEC．
7．（3分）实数a、b在数轴上的位置如图所示，化简+﹣的结果是（ ）
A．﹣2B．0C．﹣2aD．2b
【分析】根据＝|a|化简，然后去绝对值化简即可．
【解答】解：根据数轴知道﹣2＜a＜﹣1，1＜b＜2，
∴a+1＜0，b﹣1＞0，a﹣b＜0，
∴原式＝|a+1|+|b﹣1|﹣|a﹣b|
＝﹣（a+1）+b﹣1+a﹣b
＝﹣a﹣1+b﹣1+a﹣b
＝﹣2，
故选：A．
【点评】本题考查了二次根式的性质，绝对值的性质，掌握＝|a|是解题的关键．
8．（3分）如图，直线l1∥l2，分别与直线l交于点A，B，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝45°，则∠2的度数是（ ）
A．135°B．105°C．95°D．75°
【分析】依据l1∥l2，即可得到∠1＝∠3＝45°，再根据∠4＝30°，即可得出从∠2＝180°﹣∠3﹣∠4＝105°．
【解答】解：如图，∵l1∥l2，
∴∠1＝∠3＝45°，
又∵∠4＝30°，
∴∠2＝180°﹣∠3﹣∠4＝180°﹣45°﹣30°＝105°，
故选：B．
【点评】此题主要考查了平行线的性质，三角板的特征，角度的计算，解本题的关键是利用平行线的性质．
9．（3分）点P（﹣1，2）可由点Q（0，﹣1）经过什么变换得到（ ）
A．先向右平移1个单位长度，再向下平移3个单位长度
B．先向左平移1个单位长度，再向下平移3个单位长度
C．先向上平移3个单位长度，再向左平移1个单位长度
D．先向下平移1个单位长度，再向右平移3个单位长度
【分析】根据平移坐标的变化规律进行解答即可．
【解答】解：将点Q（0，﹣1）先向左平移1个单位长度，再向上平移3个单位长度即可得到点P（﹣1，2），
故选：C．
【点评】本题考查平移坐标变化，掌握平移坐标的变化规律是正确解答的关键．
10．（3分）如图，一个点在第一、四象限运动，在第1次，它从（0，﹣2）运动到点（1，1），用了1秒，然后以折线状向右运动，即（0，﹣2）→（1，1）→（2，﹣1）→（3，2）→…，它每运动一次需要1秒，那么第2024秒时点所在位置的坐标是（ ）
A．（2023，1）B．（2023，﹣1）C．（2024，2）D．（2024，﹣2）
【分析】仔细观察点的变化规律，利用规律写出答案即可．
【解答】解：观察图象知：移动后点的横坐标等于移动的时间，纵坐标按照1，﹣1，2，﹣2循环，
∵2024÷4＝505……4，
∴第2024秒时点所在位置的坐标是（2024，﹣2），
故选：D．
【点评】此题主要考查了数字变化规律以及坐标性质，根据已知得出质点坐标的变化规律是解题关键．
二、填空题：（每小题3分，共15分）。
11．（3分）比较大小： ＞ （填“＞”“＜”“＝”）．
【分析】首先确定﹣1与1的大小，进行比较即可求解．
【解答】解：∵4＜5＜9，
∴2＜＜3，
∴1＜﹣1＜2，
∴＞．
故答案为：＞．
【点评】此题主要考查了无理数的估算能力，此题把它们的减数变成和被减数相同的形式，然后只需比较被减数的大小．分母相同时，分子大的大．
12．（3分）若x，y都是实数，且，则x+3y的立方根为 3 ．
【分析】根据二次根式的被开方数大于等于0列式求出x的值，然后求出y的值，代入代数式求解，再根据立方根的定义解答．
【解答】解：根据题意得，x﹣3≥0且3﹣x≥0，
解得x≥3且x≤3，
所以，x＝3，
y＝8，
x+3y＝3+3×8＝27，
∵33＝27，
∴x+3y的立方根为3．
故答案为：3．
【点评】本题考查的知识点为：二次根式的被开方数是非负数，立方根的定义，根据x的取值范围求出x的值是解题的关键．
13．（3分）若第三象限内的点P（x，y）满足|x|＝2，y2＝4，则点P的坐标是 （﹣2，﹣2） ．
【分析】根据|x|＝2，y2＝4，得到x＝±2，y＝±2，结合点在第三象限的符号特点（﹣，﹣），确定坐标即可．
【解答】解：∵|x|＝2，y2＝4，
∴x＝±2，y＝±2，
∵点P（x，y）在第三象限，
∴点P的坐标是（﹣2，﹣2）．
故答案为：（﹣2，﹣2）．
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
14．（3分）如图，直线AB，CD相交于点O，射线OM平分∠AOC，若∠BOD＝80°，则∠BOM等于 140° ．
【分析】根据对顶角、角平分线的性质可得∠COM＝40°，根据邻补角的性质可得∠BOC＝100°，则可计算∠BOM的值．
【解答】解：∵∠BOD＝∠COA＝80°（对顶角），
（角平分线性质），
∠BOC＝180°﹣∠BOD＝100°（邻补角性质），
∴∠BOM＝∠BOC+∠COM＝140°．
故答案为：140°．
【点评】本题考查了对顶角、邻补角、角平分线的性质；关键在于能掌握好相关的基础知识点．
15．（3分）如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC∥BG；③若∠A＝α，则∠BDF＝180；④与∠DBE互余的角有2个，其中正确的有 ①②③ .（把你认为正确结论的序号都填上）
【分析】求出∠EBD+∠ABC＝90°，∠DBG+∠CBG＝90°，求出∠ABC＝∠GBC，根据角平分线的定义即可判断①；根据平行线的性质得出∠ABC＝∠BCG，求出∠ACB＝∠GBC，根据平行线的判定即可判断②；根据平行线的性质得出∠EBG＝∠A＝α，求出∠EBD＝∠EBG＝α，根据平行线的性质得出∠EBD+∠BDF＝180°，即可判断③；根据余角的定义即可判断④．
【解答】解：∵BD⊥BC，
∴∠DBC＝90°，
∴∠EBD+∠ABC＝180°﹣90°＝90°，∠DBG+∠CBG＝90°，
∵BD平分∠EBG，
∴∠EBD＝∠DBG，
∴∠ABC＝∠GBC，
即BC平分∠ABG，故①正确；
∵AE∥CF，
∴∠ABC＝∠BCG，
∵CB平分∠ACG，
∴∠ACB＝∠BCG，
∵∠ABC＝∠GBC，
∴∠ACB＝∠GBC，
∴AC∥BG，故②正确；
∵AC∥BG，∠A＝α，
∴∠EBG＝∠A＝α，
∵∠EBD＝∠DBG，
∴∠EBD＝∠EBG＝α，
∵AB∥CF，
∴∠EBD+∠BDF＝180°，
∴∠BDF＝180°﹣∠EBD＝180°﹣，故③正确；
与∠DBE互余的角有∠ABC，∠CBG，∠ACB，∠BCG，共4个，故④错误；
故答案为：①②③．
【点评】本题考查了平行线的性质和判定，角平分线的定义等知识点，能灵活运用定理进行推理是解此题的关键．
三、解答题：（本题共8小题，共75分）。
16．（8分）如图，已知∠AOB，点P是OA边上的一点．
（1）在OA的右侧作∠APC＝∠AOB（用尺规作图法，保留作图痕迹，不写作法）；
（2）在（1）的条件下，判断直线PC与直线OB的位置关系，并说明理由．
【分析】（1）根据作一个角等于已知角的方法，即可得到∠APC；
（2）根据同位角相等，两直线平行，即可得到直线PC与直线OB的位置关系．
【解答】解：（1）如图，∠APC就是所要求作的角；
（2）直线PC与直线OB的位置关系为：PC∥OB，
理由如下：
由（1）作图可得：∠APC＝∠AOB，
∴PC∥OB．
【点评】本题考查了基本作图以及平行线的判定定理，正确运用作一个角等于已知角的方法是关键．
17．（8分）计算：
（1）﹣12024﹣|﹣5|+；
（2）．
【分析】（1）先计算有理数的乘方，绝对值和开立方，再计算加减即可；
（2）将x2系数化为1，然后利用平方根的性质求解．
【解答】解：（1）﹣12024﹣|﹣5|+
＝
＝
＝；
（2），
x2＝36，
x＝±6．
【点评】本题考查了有理数的乘方，绝对值，开立方，平方根的应用，熟练掌握运算法则是解题的关键．
18．（10分）已知：如图所示，∠ABC＝∠ADC，BF和DE分别平分∠ABC和∠ADC，∠AED＝∠EDC．求证：ED∥BF．
证明：∵BF和DE分别平分∠ABC和∠ADC（已知）
∴∠EDC＝ ∠ADC，
∠FBA＝ ∠ABC． （角平分线定义）
又∵∠ADC＝∠ABC（已知），
∴∠ EDC ＝∠FBA（等量代换）．
又∵∠AED＝∠EDC（已知），
∴∠ FBA ＝∠ AED （等量代换），
∴ED∥BF（ 同位角相等，两直线平行 ）．
【分析】据几何证明题的格式和有关性质定理，填空即可．
【解答】证明：∵BF和DE分别平分∠ABC和∠ADC（已知）
∴∠EDC＝∠ADC，
∠FBA＝∠ABC（角平分线定义）．
又∵∠ADC＝∠ABC（已知），
∴∠EDC＝∠FBA（等量代换）．
又∵∠AED＝∠EDC（已知），
∴∠FBA＝∠AED（等量代换），
∴ED∥BF（同位角相等，两直线平行）．
故答案为：；；（角平分线定义）；EDC；FBA；AED；同位角相等，两直线平行．
【点评】此题考查了平行线的判定与性质，用到的知识点是平行线的判定与性质、角平分线定义，要掌握几何证明题的格式，会注明理由．
19．（8分）如图所示，已知AB∥DE，∠ABC＝80°，∠CDE＝140°，求∠BCD的度数．
【分析】过点C作FG∥AB，根据平行线的传递性得到FG∥DE，根据平行线的性质得到∠B＝∠BCF，∠CDE+∠DCF＝180°，根据已知条件等量代换得到∠BCF＝80°，由等式性质得到∠DCF＝40°，于是得到结论．
【解答】解：过点C作FG∥AB，
因为FG∥AB，AB∥DE，
所以 FG∥DE，
所以∠B＝∠BCF，（两直线平行，内错角相等 ）
∠CDE+∠DCF＝180°，（两直线平行，同旁内角互补）
又因为∠B＝80°，∠CDE＝140°，
所以∠BCF＝80°，（等量代换）
∠DCF＝40°，（等式性质）
所以∠BCD＝40°．
【点评】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①同们角相等⇔两直线平行，②内错角相等⇔两直线平行，③同旁内角互补⇔两直线平行．
20．（10分）如图，直线AB和CD相交于点O，OE把∠AOC分成两部分，且∠AOE：∠EOC＝3：5，OF平分∠BOE．
（1）若∠BOD＝72°，求∠BOE．
（2）若∠BOF＝2∠AOE+15°，求∠COF．
【分析】（1）根据对顶角相等，可得∠AOC的度数，根据∠AOE：∠EOC＝3：5，可得∠AOE，根据邻补角，可得答案；
（2）根据角平分线的定义，可得∠BOE＝2∠BOF＝4∠AOE+30°，根据邻补角的关系，可得关于∠AOE的方程，求出∠AOE的度数，可得答案．
【解答】解：（1）由对顶角相等，得∠AOC＝∠BOD＝72°，
由OE把∠AOC分成两部分且∠AOE：∠EOC＝3：5，得∠AOE＝∠AOC×＝27°，
由邻补角，得∠BOE＝180°﹣∠AOE＝180°﹣27°＝153°；
（2）由OF平分∠BOE，得∠BOE＝2∠BOF＝4∠AOE+30°．
由邻补角，得∠BOE+∠AOE＝180°，即4∠AOE+30°+∠AOE＝180°，
解得∠AOE＝30°．
∴∠EOC＝50°，∠EOF＝∠BOF＝75°，
∴∠COF＝75°﹣50°＝25°．
【点评】本题考查了对顶角、邻补角，（1）利用了对顶角相等，邻补角互补，（2）利用了角平分线的定义，邻补角互补的性质，角的和差．
21．（10分）在平面直角坐标系中，A，B，C三点的坐标分别为（﹣6，7）、（﹣3，0）、（0，3）．
（1）画出△ABC，并求△ABC的面积；
（2）在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出点A′，B′的坐标；
（3）P（﹣3，m）为△ABC中一点，将点P向右平移4个单位后，再向上平移6个单位得到点Q（n，﹣3），则m＝ ﹣9 ，n＝ 1 ．
【分析】（1）根据各点在坐标系中的位置描出各点，并顺次连接即可；
（2）根据图形平移的性质画出平移后的△A′B′C′，并写出点A′，B′的坐标即可；
（3）根据点平移的性质即可得出m、n的值．
【解答】解：（1）如图，△ABC即为所求；
S△ABC＝6×7﹣×6×4﹣×7×3﹣×3×3＝15．
（2）如图，△A′B′C′即为所求，A′（﹣1，8），B′（2，1）；
（3）∵P（﹣3，m）为△ABC中一点，将点P向右平移4个单位后，再向上平移6个单位得到点Q（n，﹣3），
∴n＝﹣3+4＝1，m+6＝﹣3，
∴n＝1，m＝﹣9．
故答案为：﹣9，1．
【点评】本题考查的是作图﹣平移变换，熟知图形平移不变性的性质是解答此题的关键．
22．（10分）已知有理数﹣3，1．
（1）在如图所示的数轴上，标出表示这两个数的点，并分别用A，B表示．
（2）若|m|＝2，在数轴上表示数m的点介于点A，B之间；表示数n的点在点A右侧且到点B距离为6．
①计算：m＝ ﹣2 ，n＝ 7
②解关于x的不等式mx+3＜n，并把解集表示在所给数轴上．
【分析】（1）根据题意，在数轴上标出点A和点B即可；
（2）①根据题意，可以求得m、n的值；
②根据m、n的值和解不等式的方法，可以解答本题．
【解答】解：（1）如下图所示，
；
（2）①∵若|m|＝2，在数轴上表示数m的点介于点A，B之间，
∴m＝﹣2，
∵示数n的点在点A右侧且到点B距离为6，
∴n＝1+6＝7，
故答案为：﹣2，7；
②由①知：m＝﹣2，n＝7，
∴不等式mx+3＜n可变为﹣2x+3＜7，
解得x＞﹣2，
其解集在数轴上表示如下所示：
．
【点评】本题考查解一元一次不等式、在数轴上表示不等式的解集，解答本题的关键是明确解一元一次不等式的方法．
23．（11分）【阅读材料】
在“相交线与平行线”的学习中，有这样一道典型问题：
如图①，AB∥CD，点P在AB与CD之间，可得结论：∠BAP+∠APC+∠PCD＝360°．
理由如下：
过点P作PQ∥AB．
∴∠BAP+∠APQ＝180°．
∵AB∥CD，
∴PQ∥CD．
∴∠PCD+∠CPQ＝180°．
∴∠BAP+∠APC+∠PCD
＝∠BAP+∠APQ+∠CPQ+∠PCD
＝180°+180°
＝360°．
【问题解决】
（1）如图②，AB∥CD，点P在AB与CD之间，可得∠BAP，∠APC，∠PCD间的等量关系是 ∠APC＝∠A+∠C ；（只写结论）
（2）如图③，AB∥CD，点P，E在AB与CD之间，AE平分∠BAP，CE平分∠DCP．写出∠AEC与∠APC间的等量关系，并写出理由；
（3）如图④，AB∥CD，点P，E在AB与CD之间，∠BAE＝∠BAP，∠DCE＝∠DCP，可得∠AEC与∠APC间的等量关系是 ∠APC+3∠AEC＝360° （只写结论）
【分析】（1）如图②中，结论：∠APC＝∠A+∠C．作PE∥AB，利用平行线的性质证明即可．
（2）结论：∠APC＝2∠AEC．如图③中，设∠EAB＝∠EAP＝x，∠ECD＝∠ECP＝y．利用（1）中结论证明即可．
（3）结论：∠APC+3∠AEC＝360°，利用题目中的基本结论解决问题即可．
【解答】解：（1）如图②中，结论：∠APC＝∠A+∠C．
理由：作PE∥AB，
∵AB∥CD，AB∥PE，
∴CD∥PE，
∴∠APE＝∠A，∠C，
∴∠APC＝∠APE+∠CPE＝∠A+∠C．
故答案为∠APC＝∠A+∠C．
（2）结论：∠APC＝2∠AEC．
理由：如图③中，设∠EAB＝∠EAP＝x，∠ECD＝∠ECP＝y．
由（1）可知：∠AEC＝x+y，∠APC＝2x+2y，
∴∠APC＝2∠AEC．
（3）如图④中，设∠EAB＝x，∠DCE＝y，则∠BAP＝3x，∠DCP＝3y，
由题意：∠AEC＝x+y，∠APC+3x+3y＝360°，
∴∠APC+3∠AEC＝360°，
故答案为：∴∠APC+3∠AEC＝360°，
【点评】本题考查平行线的判定和性质，解题的关键是需要添加常用辅助线，构造平行线解决问题，属于中考常考题型．