广东省中山市第一中学教育集团2023-2024学年七年级下学期期中考试数学试题

这是一份广东省中山市第一中学教育集团2023-2024学年七年级下学期期中考试数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

参考答案与试题解析
一、选择题（共10小题，每题3分，共30分）
1．【解答】解：如图，可以通过平移节水标志得到的图形是．
故选：A．
2．【解答】解：∵1＞0，﹣2＜0，
∴在平面直角坐标系中，点（1，﹣2）所在的象限是第四象限．
故选：D．
3．【解答】解：A．3.14是有限小数，属于有理数，故本选项不符合题意；
B．是分数，属于有理数，故本选项不符合题意；
C．，是无理数，故本选项符合题意；
D．＝﹣3，是整数，属于有理数，故本选项不符合题意．
故选：C．
4．【解答】解：∵是关于x和y的二元一次方程kx﹣2y＝4的解，
∴2k﹣2×（﹣3）＝4，
解得k＝﹣1．
故选：A．
5．【解答】解：∵，即，
∴，
，
，
∴的整数部分是2，
故选：C．
6．【解答】解：由∠1＝∠3，不能判定AD∥BC，故A符合题意；
∵∠3＝∠E，
∴AD∥BC，
故B不符合题意；
∵∠2＝∠B，
∴AD∥BC，
故C不符合题意；
∵∠BCD+∠D＝180°，
∴AD∥BC，
故D不符合题意；
故选：A．
7．【解答】解：相等的角不一定是对顶角，故A是假命题，不符合题意；
无限不循环小数是无理数，故B是假命题，不符合题意；
垂线段最短，故C是真命题，符合题意；
平面内，过直线外一点有且只有一条直线与已知直线平行，故D是假命题，不符合题意；
故选：C．
8．【解答】解：由题意可得，
故选：A．
9．【解答】解：如图所示，过∠2顶点作直线l∥支撑平台，直线l将∠2分成两个角∠4和∠5，
∵工作篮底部与支撑平台平行、直线l∥支撑平台，
∴直线l∥支撑平台∥工作篮底部，
∴∠1＝∠4＝30°、∠5+∠3＝180°，
∵∠4+∠5＝∠2＝50°，
∴∠5＝50°﹣∠4＝20°，
∴∠3＝180°﹣∠5＝160°，
故选：D．
10．【解答】解：∵点M（3，﹣2）与点N（x、y）在同一条平行于x轴的直线上，MN＝1，
∴y＝﹣2，|x﹣3|＝1，
∴x＝2或4，
∴N点的坐标为（2，﹣2）或（4，﹣2）．
故选：D．
二、填空题（共6小题，每小题3分，共18分）
11．【解答】解：25的立方根是．
故答案为：．
12．【解答】解：方程2x﹣3y＝6，
解得：y＝，
故答案为：
13．【解答】解：∵点P在第四象限，且点P到x轴的距离是3，到y轴的距离是2，
∴点P的横坐标是2，纵坐标是﹣3，
∴点P的坐标为（2，﹣3）．
故答案为：（2，﹣3）．
14．【解答】解：（1）∵B的坐标为（6，0），
∴OB＝6，
∵CB＝，
∴OC＝6﹣＝，
∵△OAB沿x轴向右平移得到△CDE，
∴OC＝BE＝，
∴OE＝OB+BE＝6+＝；
故答案为：；
（2）连结AD，如图，
∵△OAB沿x轴向右平移得到△CDE，
∴AD＝OC＝BE＝，AD∥OC，
∵点A的坐标为（2，4），
∴点A到x轴的距离为4，
∴四边形OADE的面积＝×4×（+）＝30．
故答案为：15．
15．【解答】解：∵a※b＝，
∴a※b﹣b※a
＝（ab﹣a+b）﹣（ab﹣b+a）
＝ab﹣a+b﹣ab+b﹣a
＝﹣a+b
＝﹣（a﹣b），
∵a﹣b＝2024，
∴a※b﹣b※a
＝﹣（a﹣b）
＝﹣×2024
＝﹣3036．
故答案为：﹣3036．
16．【解答】解：如图，过点A1，A4，A7，A10，A13，……A2024分别作x轴的垂线，
∵△A1A2O是边长为2正三角形，
∴OB＝BA2＝1，A1B＝＝，
∴点A1横坐标为1，
由题意可得，点A2横坐标为2，点A3横坐标为3，点A4横坐标为4，…
因此点A2024横坐标为2024，
∵2024÷3＝674……2，而674是偶数，
∴点A2024在x轴，
∴点A2024的纵坐标为0，
即点A2024（2024，0），
故答案为：（2024，0）．
三、解答题（一）（共3小题，共24分）
17．【解答】解：（1）
＝﹣2﹣（﹣1）+4
＝﹣2﹣+1+4
＝3﹣．
（2），
①﹣②，可得x＝10，
把x＝10代入①，可得：3×10﹣y＝8，
解得y＝44，
∴原方程组的解是．
18．【解答】解：（1）如图所示：
（2）点A1，B1，C1的坐标分别为：（0，4），（﹣1，1），（3，1）；
故答案为：（0，4），（﹣1，1），（3，1）；
（3）设P（0，y），根据题意得：
，
解得：|h|＝3，
∴h＝±3，
∴y的值为：3﹣2或﹣3﹣2，即1或﹣5，
∴P（0，1）或（0，﹣5）．
故答案为：P（0，1）或（0，﹣5）．
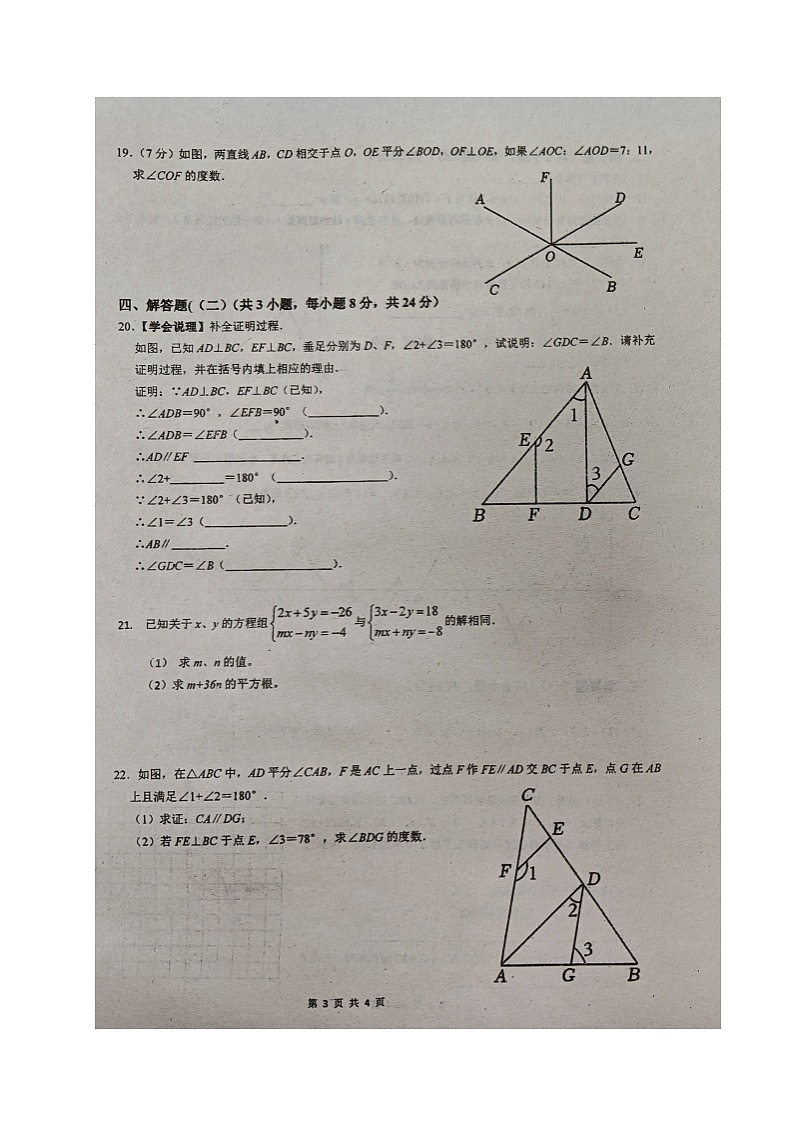
19．【解答】解：因为∠AOC：∠AOD＝7：11，且∠AOC+∠AOD＝180°，
所以∠AOC＝70°，∠AOD＝110°．
又因为∠DOB和∠AOC是对顶角，
所以∠BOD＝∠AOC＝70°．
因为OE平分∠BOD，
所以∠DOE＝．
因为OF⊥OE，
所以∠DOF＝90°﹣∠DOE＝55°，
所以∠COF＝180°﹣∠DOF＝125°．
四、解答题（（二）（共3小题，每小题8分，共24分）
20．【解答】解：∵AD⊥BC，EF⊥BC（已知），
∴∠ADB＝90°，∠EFB＝90°（垂直的定义）
∴∠ADB＝∠EFB（等量代换），
∴AD∥EF（同位角相等，两直线平行）．
∴∠2+∠1＝180°（两直线平行，同旁内角互补）
∵∠2+∠3＝180°（已知）．
∴∠1＝∠3（同角的补角相等）．
∴AB∥DG（内错角相等，两直线平行）
∴∠GDC＝∠B（两直线平行，同位角相等）．
故答案为：垂直的定义；等量代换；同位角相等，两直线平行；∠1；两直线平行，同旁内角互补；同角的补角相等；DG；两直线平行，同位角相等．
21．【解答】解：（1）根据题意得：
，
①×2得：4x+10y＝﹣52③，
②×5得：15x﹣10y＝90④，
③+④得：19x＝38，
x＝2，
把x＝2代入①得：y＝﹣6，
把x＝2，y＝﹣6分别代入mx﹣ny＝﹣4和mx+ny＝﹣8得：
，
①+②得：m＝﹣3，
把m＝﹣3代入①得：，
∴；
（2）由（1）可知：m＝﹣3，，
∴，
∴9的平方根为±3，
答：m+36n 的平方根为±3．
22．【解答】（1）证明：∵FE∥AD，
∴∠1+∠CAD＝180°，
又∵∠1+∠2＝180°，
∴∠CAD＝∠2，
∴CA∥DG；
（2）解：由（1）可知CA∥DG，
∴∠CAB＝∠3＝78°，∠BDG＝∠C，
∵AD平分∠CAB，
∠CAD＝∠CAB＝×78°＝39°，
∵FE∥AD，
∴∠CFE＝∠CAD＝39°，
∵FE⊥BC于点E，
∴∠C＝90°﹣∠CFE＝90°﹣39°＝51°，
∴∠BDG＝∠C＝51°．
五、解答题（（三）（共2小题，每小题12分，共24分）
23．【解答】解：（1）由题意得：415﹣400＝15（米），
87×2+2π（36+1.2×7）≈453（米），
答：第三圈半圆形弯道长比第一圈半圆形弯道长多15米，小王计算的第八圈长约453米；
（2）设小王的平均速度为x米/秒，邓教练的平均速度为y米/秒，
由题意得：，
解得：，
答：小王的平均速度为米/秒，邓教练的平均速度为米/秒．
24．【解答】（1）解：EF∥CD，理由如下：∵∠1＝∠2，∴AB∥EF，
∴∠AEF＝∠MAE，
∵∠MAE＝45°，∠FEG＝15°
∴∠AEG＝60°，
∵EG平分∠AEC，
∴∠CEG＝∠AEG＝60°，
∴∠CEF＝∠CEG+∠FEG＝75°，∠NCE＝75°，
∴∠NCE＝∠CEF，
∴EF∥CD．
（2）解：∵∠1＝∠2，
∴AB∥EF，
∴∠FEA+∠MAE＝180°，∠MAE＝140°，
∴∠FEA＝40°，∠FEG＝30°，
∴∠AEG＝70°，
∵EG平分∠AEC，
∴∠CEG＝∠AEG＝70°，
∴∠FEC＝100°，
∵AB∥CD，
∴EF∥CD，
∴∠NCE+∠FEC＝180°，
∴∠NCE＝80°．
（3）证明：∵∠1＝∠2，
∴AB∥EF，
∴∠MAE+∠FEA＝180°，
∴∠FEA＝180°﹣∠MAE，
∴∠AEG＝∠FEA+∠FEG＝180°﹣∠MAE+∠FEG，
∵EG平分∠AEC，
∴∠GEC＝∠AEG，
∴∠FEC＝∠GEC+∠FEG＝180°﹣∠MAE+∠FEG+∠FEG＝180°﹣∠MAE+2∠FEG，
∵AB∥CD，AB∥EF，
∴EF∥CD，
∴∠FEC+∠NCE＝180°，
∴180°﹣∠MAE+2∠FEG+∠NCE＝180°，
∴2∠FEG+∠NCE＝∠MAE，
即∠NCE＝∠MAE﹣2∠FEG．