广东省广州科学城中学2023-2024学年高一下学期期中检测数学试题

这是一份广东省广州科学城中学2023-2024学年高一下学期期中检测数学试题，文件包含广东省广州科学城中学2023-2024学年高一下学期期中考试数学试题docx、广东省广州科学城中学2023-2024学年高一下学期期中考试数学试题pdf等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

本试卷共4页，22小题，满分150分。考试用时120分钟。
注意事项：1．答卷前，考生务必用黑笔将个人信息准确填写在答题卡上，并用2B铅笔在答题卡上规定位置涂黑自己的考生号。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
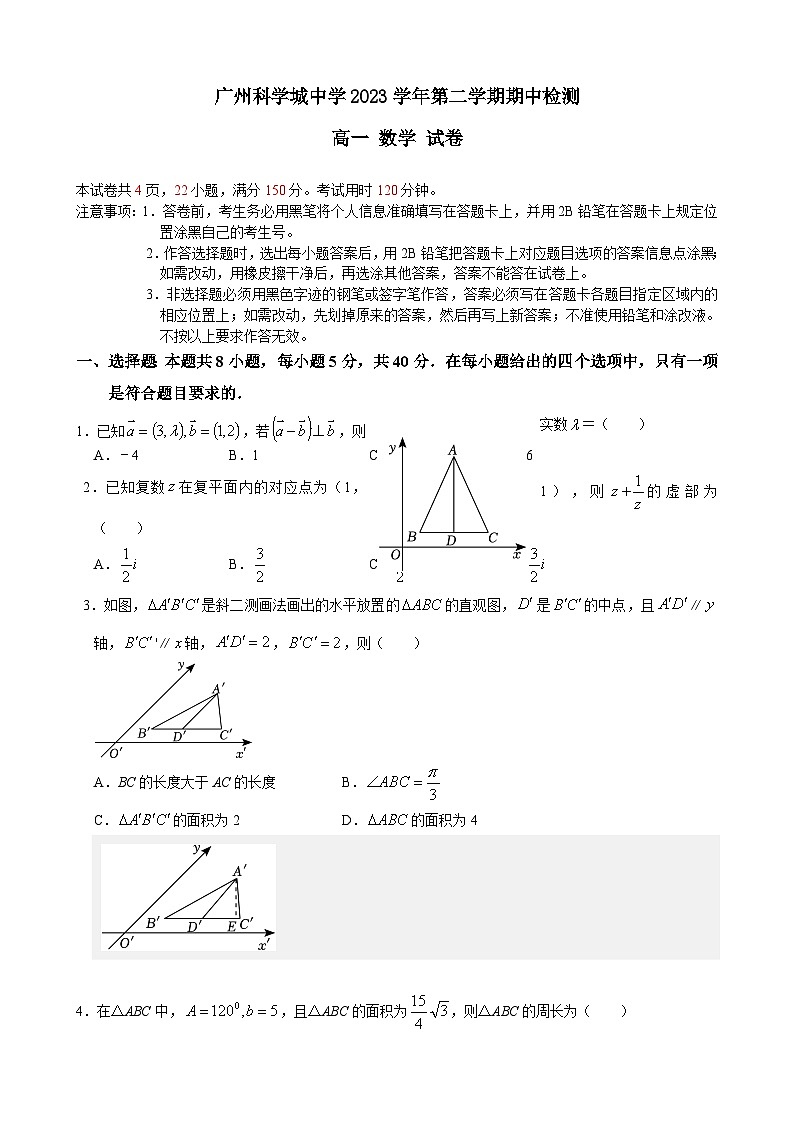
1．已知，若，则实数＝（ ）
A．﹣4B．1C．2D．6
2．已知复数在复平面内的对应点为（1，1），则的虚部为（ ）
A．B．C．D．
3．如图，是斜二测画法画出的水平放置的的直观图，是的中点，且∥轴，'∥轴，，，则（ ）
A．BC的长度大于AC的长度 B．
C．的面积为2 D．的面积为4

4．在△ABC中，，且△ABC的面积为，则△ABC的周长为（ ）
A．15B．12C．16D．20
5．若正三棱台的上、下底面的边长分别为3和6，侧棱长为2，则其体积为（ ）
A．B．C．D．
6．已知是夹角为120°的两个单位向量，若向量在向量上的投影向量为，则＝（ ）
A．B．C．﹣2D．2
7．已知分别是的边的中点，且，有下列四个等式：①；②；③；④．其中正确的等式的序号是（ ）
A. ①③ B. ①②④ C. ②③ D. ②③④
8．已知函数，若方程在区间内的解为，则（ ）
A．B．C．D．
二、选择题：本题共4小题，每小题5分， 共计20分．在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9．已知复数z的共轭复数为，则下列命题正确的是（ ）
A．B．为纯虚数
C．D．
10．已知直线l，m，平面α，β，则下列说法错误的是（ ）
A．m∥l，l∥α，则m∥α
B．l∥β，m∥β，l⊂α，m⊂α，则α∥β
C．l∥m，l⊂α，m⊂β，则α∥β
D．l∥β，m∥β，l⊂α，m⊂α，l∩m＝M，则α∥β
11．已知向量满足，且，则（ ）
A．B． C．D．
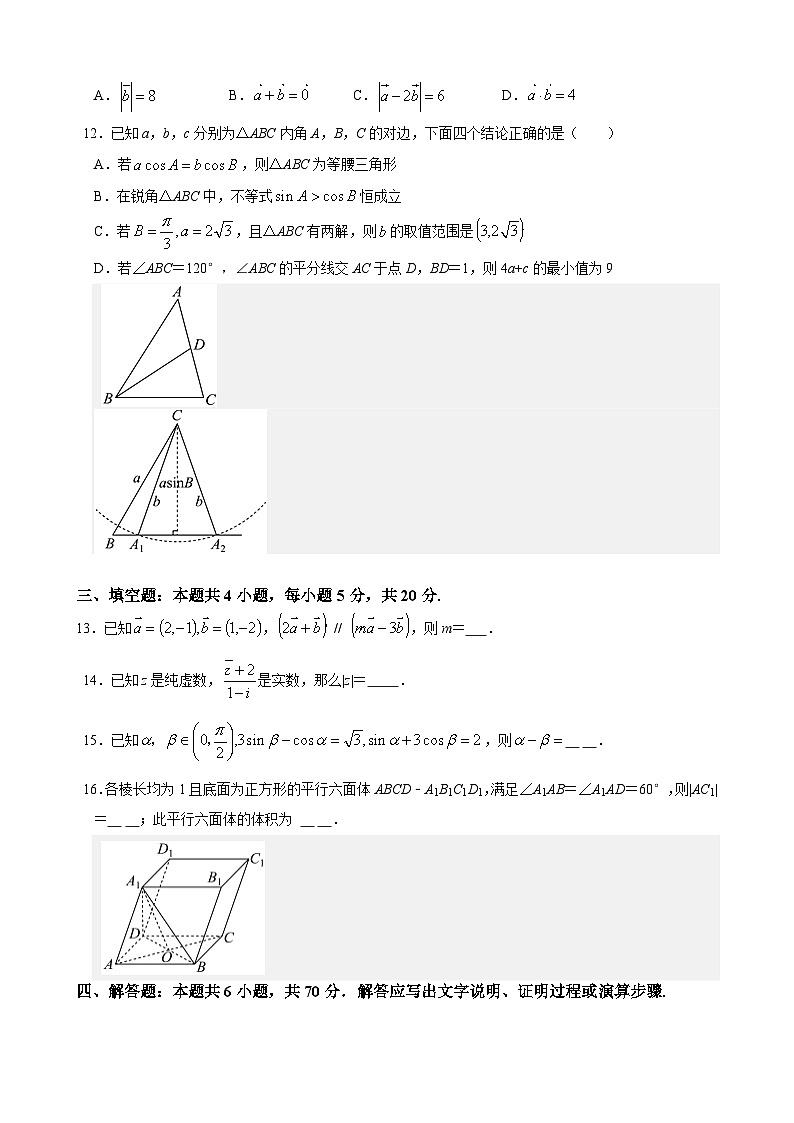
12．已知a，b，c分别为△ABC内角A，B，C的对边，下面四个结论正确的是（ ）
A．若，则△ABC为等腰三角形
B．在锐角△ABC中，不等式恒成立
C．若，且△ABC有两解，则的取值范围是
D．若∠ABC＝120°，∠ABC的平分线交AC于点D，BD＝1，则4a+c的最小值为9

填空题：本题共4小题，每小题5分，共20分.
13．已知， // ，则m＝ ．
14．已知z是纯虚数，是实数，那么|z|＝ ．
15．已知，则 ．
16．各棱长均为1且底面为正方形的平行六面体ABCD﹣A1B1C1D1，满足∠A1AB＝∠A1AD＝60°，则|AC1|＝ ；此平行六面体的体积为 ．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.
17．（10分）已知复数，，，且为纯虚数，求复数．
18．（12分）在中，角所对的边分别是，已知.
（1）求角的大小；
（2）若，求的值.
19．（12分）某校学生利用解三角形有关知识进行数学实践活动．A处有一栋大楼，某学生选B，C两处作为测量点，测得BC的距离为50m，∠ABC＝45°，∠BCA＝105°，在C处测得大楼楼顶D的仰角α为75°．
（1）求A，C两点间的距离；
（2）求大楼的高度．
20．（12分）已知在直角三角形ABC中，AC⊥BC，BC＝2，．
（1）若以AC为轴，直角三角形ABC旋转一周，求所得几何体的表面积；
（2）一只蚂蚁在问题（1）形成的几何体上从点B绕着几何体的侧面爬行一周回到点B，求蚂蚁爬行的最短距离．
21．（12分）如图，在平行六面体ABCD﹣A1B1C1D1中，M为DD1的中点，N为CC1的中点．
（1）求证：BD1∥平面MAC；
（2）求证：平面NBD1∥平面MAC．
（12分）已知．
（1）求f（x）的单调递增区间与对称中心；
（2）当时，f（x）的取值范围为，求实数a的取值范围．
广州科学城中学2023学年第二学期期中检测
高一 数学 试卷

本试卷共4页，22小题，满分150分。考试用时120分钟。
注意事项：1．答卷前，考生务必用黑笔将个人信息准确填写在答题卡上，并用2B铅笔在答题卡上规定位置涂黑自己的考生号。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知，若，则实数＝（ ）
A．﹣4B．1C．2D．6
【解答】解：，
则，，
则，解得．故选：B．
2．已知复数在复平面内的对应点为（1，1），则的虚部为（ ）
A．B．C．D．
【解答】解：因为复数z在复平面内的对应点为（1，1），所以，
，所以虚部为．
故选：C．
3．如图，是斜二测画法画出的水平放置的的直观图，是的中点，且∥轴，'∥轴，，，则（ ）
A．BC的长度大于AC的长度 B．
C．的面积为2 D．的面积为4
【解答】解：由图象知：BC＝B'C'＝2，AD＝2A'D'＝4，AD⊥BC，D为BC的中点
所以，A错误；，所以，B错误；
因为∠A'D'C'＝45°，A'D'＝2，
所以的上的高，的面积，C错误，
△ABC的面积，D正确．故选：D．
4．在△ABC中，，且△ABC的面积为，则△ABC的周长为（ ）
A．15B．12C．16D．20
【解答】解：因为A＝120°，b＝5，且△ABC的面积为，
所以，解得c＝3，
由余弦定理，
所以a＝7，则C△ABC＝a+b+c＝15．
故选：A．
5．若正三棱台的上、下底面的边长分别为3和6，侧棱长为2，则其体积为（ ）
A．B．C．D．
【解答】解：正三棱台ABC﹣A1B1C1上下底面的中心为D1，D，连接A1D1，AD，DD1，
过A1作A1E⊥AD交于E点，
∵A1B1＝3，AB＝6，∴，
∵DD1垂直于上下底面，且A1E⊥AD，∴∠A1ED＝∠EDD1＝∠DD1A1＝90°，
∴四边形A1EDD1为矩形，∴，
又，∴，∴DD1＝1，
又，，
∴三棱台的体积为．
故选：A．
6．已知是夹角为120°的两个单位向量，若向量在向量上的投影向量为，则＝（ ）
A．B．C．﹣2D．2
【解答】解：是夹角为120°的两个单位向量，
则，
向量在向量上的投影向量为，
则，
即，即，解得．故选：D．
7．已知分别是的边的中点，且，有下列四个等式：①；②；③；④．其中正确的等式的序号是（ ）
A. ①③ B. ①②④ C. ②③ D. ②③④
【解答】对于①：，①不正确；
对于②：，②正确；
对于③：，③正确；
对于④：
，④正确。故选：D
8．已知函数，若方程在区间内的解为，则（ ）
A．B．C．D．
【解答】解：由解得，
当k＝0时，对称轴为，
当k＝1时，对称轴为，
由得x1，x2关于对称．
则x1+x2＝×2＝，x2＝﹣x1，其中sin（2x1﹣）＝，
则sin（x1﹣x2）＝sin（x1﹣+x1）＝sin（2x1﹣）＝sin（2x1﹣﹣）＝﹣sin[﹣（2x1﹣）]＝﹣cs（2x1﹣）＝，故选：C．
二、选择题：本题共4小题，每小题5分， 共计20分．在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9．已知复数z的共轭复数为，则下列命题正确的是（ ）
A．B．为纯虚数
C．D．
【解答】解：设复数，则，
故，A正确；
，当b＝0时，为实数，B错误；
，则，C正确；
故，则，D正确．
故选：ACD．
10．已知直线l，m，平面α，β，则下列说法错误的是（ ）
A．m∥l，l∥α，则m∥α
B．l∥β，m∥β，l⊂α，m⊂α，则α∥β
C．l∥m，l⊂α，m⊂β，则α∥β
D．l∥β，m∥β，l⊂α，m⊂α，l∩m＝M，则α∥β
【解答】解：选项A中，m可能在α内，也可能与α平行，故A错误；
选项B中，α与β也可能相交，故B错误；
选项C中，α与β也可能相交，故C错误；
选项D中，依据面面平行的判定定理可知α∥β，故D正确．故选：ABC．
11．已知向量满足，且，则（ ）
A．B． C．D．
【解答】解：因为，所以，
即，整理可得①，
再由，且可得，所以，，故A、D错误；
所以，即向量的夹角，
故向量共线且方向相反，所以，故B正确；
又，所以，故C正确．故答案为：BC．
12．已知a，b，c分别为△ABC内角A，B，C的对边，下面四个结论正确的是（ ）
A．若，则△ABC为等腰三角形
B．在锐角△ABC中，不等式恒成立
C．若，且△ABC有两解，则的取值范围是
D．若∠ABC＝120°，∠ABC的平分线交AC于点D，BD＝1，则4a+c的最小值为9
【解答】解：选项A，因为，由正弦定理可得：，
所以有a2（b2+c2﹣a2）＝b2（a2+c2﹣b2），整理可得（a2﹣b2）（a2+b2﹣c2）＝0，
所以a＝b或a2+b2＝c2，
故△ABC为等腰三角形或直角三角形，故A错误；
选项B，若△ABC为锐角三角形，所以，所以，
由正弦函数在单调递增，则，故B正确．
选项C，如图，若△ABC有两解，则，
所以，则b的取值范围是，故C正确．
选项D，∠ABC的平分线交AC于点D，BD＝1，
由S△ABC＝S△ABD+S△BCD，由角平分线性质和三角形面积公式得，
得，
即ac＝a+c，得，
得，
当且仅当，即c＝2a＝3时，取等号，故D正确．
故选：BCD．
填空题：本题共4小题，每小题5分，共20分.
13．已知， // ，则m＝ ﹣6 ．
【解答】解：因为，且 // ，
所以，，
可得5（6﹣m）﹣（﹣4）（2m﹣3）＝0，解得m＝﹣6．故答案为：﹣6．
14．已知z是纯虚数，是实数，那么|z|＝ 2 ．
【解答】解：设，则，
，则b＝2，
那么|z|＝2．故答案为：2．
15．已知，则 ．
【解答】解：已知① ②
由①2+②2可得：，则，
又，即，则．
故答案为：．
16．各棱长均为1且底面为正方形的平行六面体ABCD﹣A1B1C1D1，满足∠A1AB＝∠A1AD＝60°，则|AC1|＝ ；此平行六面体的体积为 ．
【解答】解：，
∴
＝1+1+1+2•cs∠A1AB+2•cs∠DAB+2•cs∠CBB1
＝3+2×1×1×+0+2×＝5，
∴|AC1|＝，
连接AB，CD交于点O，连接A1O，
∵底面是边长是1的正方体，
∴|AO|＝＝，|DO|＝|BD|＝，
∵∠A1AB＝∠A1AD＝60°，连接A1D，A1B，则|A1D|＝|A1B|＝1，
∴在△A1DB中，A1O⊥BD，∴|A1O|＝＝，
∵|A1O|2+|AO|2＝|A1A|2，∴A1O⊥AO，
AO∩BD＝O，∴A1O⊥平面ABCD，
∴平行六面体的体积为V＝SABCD•A1O＝1×＝．
故答案为：；．
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.
17．（10分）已知复数，，，且为纯虚数，求复数．
【解答】
解：，
因为为纯虚数，所以，，
18．（12分）在中，角所对的边分别是，已知.
（1）求角的大小；
（2）若，求的值.
【解答】
解：（1），由正弦定理得，
在中，均不为0，，
又，.
（2）)在中，，
，
==，
.
19．（12分）某校学生利用解三角形有关知识进行数学实践活动．A处有一栋大楼，某学生选B，C两处作为测量点，测得BC的距离为50m，∠ABC＝45°，∠BCA＝105°，在C处测得大楼楼顶D的仰角α为75°．
（1）求A，C两点间的距离；
（2）求大楼的高度．
【解答】
解：（1）在△ABC中，∠BAC＝180°﹣105°﹣45°＝30°，
根据正弦定理可知：，则，
所以；
（2），
在△DCA中，因为DA⊥AC，则，
所以
∴．
20．（12分）已知在直角三角形ABC中，AC⊥BC，BC＝2，．
（1）若以AC为轴，直角三角形ABC旋转一周，求所得几何体的表面积；
（2）一只蚂蚁在问题（1）形成的几何体上从点B绕着几何体的侧面爬行一周回到点B，求蚂蚁爬行的最短距离．
【解答】解：（1）在Rt△ABC中，BC＝2，，
所以，解得，
若以AC为轴旋转一周，则形成的几何体为以BC＝2为半径，高为的圆锥，
则，
所以圆锥的表面积为；
（2）由问题（1）的圆锥，要使蚂蚁爬行的距离最短，
则沿点B的母线把圆锥侧面展开为平面图形，最短距离就是点B到点B1的距离，
设,因为弧的长等于圆锥底面圆的周长，即，
又因为弧的长为，所以，即，
在△ABB1中，由余弦定理得，即
即蚂蚁爬行的最短距离为．
21．（12分）如图，在平行六面体ABCD﹣A1B1C1D1中，M为DD1的中点，N为CC1的中点．
（1）求证：BD1∥平面MAC；
（2）求证：平面NBD1∥平面MAC．
【解答】
证明：（1）连接BD，交AC于O，连接MO，
在平行六面体ABCD﹣A1B1C1D1中，ABCD为平行四边形，
所以O为BD中点，
因为M为DD1的中点，所以MO∥BD1，
因为MO⊂平面MAC，BD1⊄平面MAC，
所以BD1∥平面MAC；
（2）在平行六面体ABCD﹣A1B1C1D1中，CC1∥DD1，CC1＝DD1，
因为M为DD1的中点，N为CC1的中点，
所以CN∥MD1，CN＝MD1，
所以四边形NCMD1为平行四边形，从而MC∥D1N，
因为MC⊂平面MAC，D1N⊄平面MAC，
所以D1N∥平面MAC，
由（1）可知：BD1∥平面MAC，
因为D1N⊂平面NBD1，BD1⊂平面NBD1，且BD1∩D1N＝D1，
所以平面NBD1∥平面MAC．
（12分）已知．
（1）求f（x）的单调递增区间与对称中心；
（2）当时，f（x）的取值范围为，求实数a的取值范围．
【解答】
解：（1）
令，解得，
令，解得，
所以f（x）的单调递增区间为，对称中心为；
（2）的函如图所示：
由题意当时，f（x）的取值范围为，
故当且仅当x1≤a≤x2，其中，，
令，得，即，
解得，
所以，
令，得，
即或，
解得或，
所以，
综上所述，满足题意的实数a的取值范围为．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/4/10 10:39:57；用户：龙骁禹；邮箱：18873024081；学号：38568318