陕西省咸阳市礼泉县2023届九年级中考一模数学试卷(含答案)

这是一份陕西省咸阳市礼泉县2023届九年级中考一模数学试卷(含答案)，共11页。试卷主要包含了本试卷分为第一部分和第二部分，领到试卷和答题卡后，请用0等内容，欢迎下载使用。

注意事项：
1.本试卷分为第一部分(选择题)和第二部分(非选择题)。全卷共6页，总分120分。考试时间120分钟。
2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号，同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B)。
3.请在答题卡上各题的指定区域内作答，否则作答无效。
4.作图时，先用铅笔作图，再用规定签字笔描黑。
5.考试结束，本试卷和答题卡一并交回。
第一部分(选择题 共24分)
一、选择题(共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的)
1. sin 45°的倒数等于
A.12 B. 2 C.1 D.22
2.如图是某几何体的三视图，该几何体是
A.圆柱 B.长方体
C.五棱柱 D.六棱柱
3.计算 (-2a)³·a²正确的是
A.2a ⁵ B.-2a⁵
C.8a⁵ D.-8a ⁵
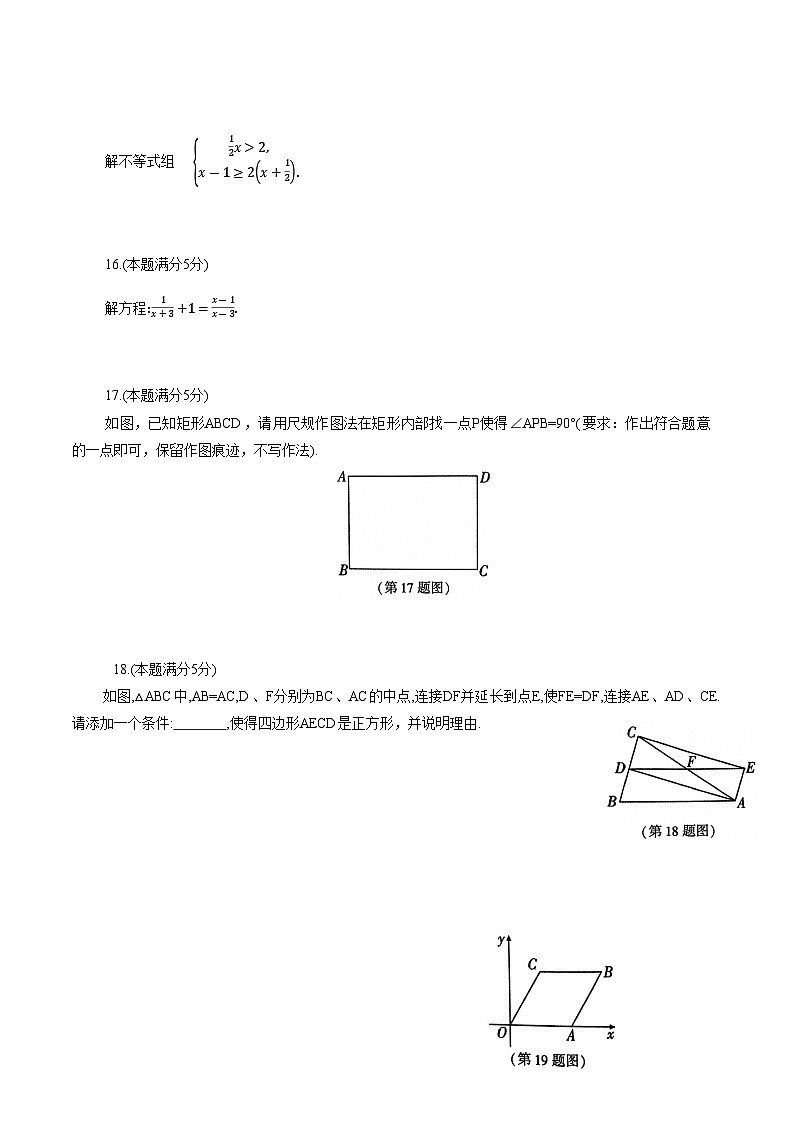
4.实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是
A. a>b B.-a>b C. a>-b D. ab>0
5.如图,在△ABC中,∠B=90°,点D是BC上一点,∠BAD=∠C, tan∠ADB=3,则sinC的值为
A.13 B.31010
C.1010 D.3
6.正比例函数y=2x与一次函数y=kx+3的图象交于点P(a,2),则关于x的不等式kx+3>2x的解集为
A. x<1 B. x>1 C. x<2 D. x>2
7.如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为M,连接AD.若 AB=8,CD=43,则AD的长为
A.10
B.5
C.43
D.35
(第7题图)
8.将抛物线y=x²-2x+1向上平移2个单位长度，再向左平移3个单位长度，得到抛物线y=x²+bx+c, 则b，c的值为
A. b=-8,c=18 B. b=8,c=14
C. b=-4,c=6 D. b=4,c=6
第二部分(非选择题 共96分)
二、填空题(共5小题，每小题3分，计15分)
9.方程 x²+3x=0的解为 .
10.若扇形的圆心角为135°,半径为4,则它的弧长为 .(结果保留π)
11.七巧板起于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术，经历代演变而成七巧板，也被誉为“东方魔板”.19世纪传到国外，被称为“唐图”.如图是由边长为8cm 的正方形ABCD薄板分为7块制作成的“七巧板”，点O是正方形的中心，点F为CD的中点,该“七巧板”中7块图形之一的正方形(阴影部分)面积为 cm².
12.如图，点A在反比例函数y=kx(x<0)的图象上，点C在x轴正半轴上，直线AC交y轴于点B,若BC=3AB,△AOC的面积为9,则k的值为 .
13.如图,在▱ABCD中,AB=AD=6,点P在▱ABCD内运动,连接PA,PB,PC,若∠APB=∠ABC=60°,则PA+PC的最大值为 .
三、解答题(共13小题，计81分.解答应写出过程)
14.(本题满分5分)
计算： π-20230-4cs30°-|12-4|.
15.(本题满分5分)
解不等式组 12x>2,x-1≥2x+12.
16.(本题满分5分)
解方程:1x+3+1=x-1x-3.
17.(本题满分5分)
如图，已知矩形ABCD，请用尺规作图法在矩形内部找一点P使得∠APB=90°(要求：作出符合题意的一点即可，保留作图痕迹，不写作法).
18.(本题满分5分)
如图,△ABC中,AB=AC,D、F分别为BC、AC的中点,连接DF并延长到点E,使FE=DF,连接AE、AD、CE.请添加一个条件: ,使得四边形AECD是正方形，并说明理由.
19.(本题满分5分)如图，在平面直角坐标系中，菱形OABC的顶点A的坐标为(4，0)，点B、C 在第一象限,∠AOC=60°,求点C的坐标.
20.(本题满分5分)
习近平总书记指出，中华优秀传统文化是中华民族的“根”和“魂”.某校为了传承中华优秀传统文化，举行“薪火传承育新人”系列活动，组建了四个活动小组：A(经典诵读)，B(诗词大赛)，C (传统故事)，D(汉字听写).学校规定：每名学生必须参加且只能参加其中一个小组.若该校小敏和小文两名同学各自从四个小组中随机选择一个小组，每一个小组被选中的可能性相同.
(1)小敏选择经典诵读小组的概率是 ;
(2)用画树状图或列表的方法，求小敏和小文选择不同小组的概率.
21.(本题满分6分)
如图，小敏在数学实践活动中，利用所学知识对某公园的摩天轮的高度PQ进行测量，她先在D处竖立一根高1米的标杆CD，沿QD后退，恰好退到点B处看到标杆顶端C和摩天轮底端Q在一条直线上，继续后退又在E处测得摩天轮顶端P的仰角∠PEQ=38.8°，小敏的眼睛到地面的距离AB=1.6米,BD=6米,EB=21.5米,已知点E,B,D,Q 在一条水平线上,AB⊥EQ,CD⊥EQ,PQ⊥EQ,求摩天轮的高PQ.(参考数据:tan 38.8°≈0.80)
22.(本题满分7分)
2023年是全面贯彻落实党的二十大精神的开局之年，是巩固拓展脱贫攻坚成果同乡村振兴有效衔接的关键之年.为稳步推进乡村建设，某地推广魔芋种植并邀请相关农业技术人员来指导当地居民种植.小林家种植魔芋，并利用魔芋开发出A，B两种产品，其售价和成本如表所示：
(1)已知第一季度A，B两种产品共销售2000袋，获利9200元.求小林家第一季度销售A产品多少袋；
(2)根据之前的销售情况，估计第二季度还能由上表中的价格销售两种产品共3600袋，其中A产品的销售量不高于1000袋.假设第二季度，销售A产品为a袋，销售这两种产品获得总利润为w元，求出w与a之间的函数关系式，并求出第二季度，小林家销售这两种产品至少获得总利润多少元.
23.(本题满分7分)
2023年2月10日，神舟十五航天员乘组圆满完成出舱活动全部既定任务.近年来，中国航天取得了丰硕的成果，中国航天正加速步入空间站时代，以实现更加广阔的太空梦想.为鼓励青少年追踪航天科技发展，勇于探索无边宇宙空间、畅想未来，某市举办“我们的太空创想”科普绘画比赛活动，特向全市八年级各班征集绘画作品，随机抽取了40个班上交的作品件数，发现各班上交作品数分别是6件，7件，8件，9件，10件这五种情形，并将统计结果绘制成了如下不完整的统计图.
根据以上信息，解答下列问题：
(1)补全条形统计图，此次所抽取班级绘画作品件数的众数为 件,中位数为 件;
(2)求此次所抽取班级上交绘画作品的平均件数；
(3)若该市八年级共有1000个班级，请估计此次绘画比赛共征集到多少件绘画作品?
24.(本题满分8分)
如图,在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC 相切于点E，连接DE并延长交BC的延长线于点F.
求证:BF=BD;
若CF=2,tan∠BDE=2,求⊙O的半径.
25.(本题满分8分)
如图，已知抛物线y=-x²-2x+3与x轴交于A、B两点(点A在点B 的左侧)，与y轴交于点C.
求点A、B、C的坐标;
(2)抛物线的对称轴l与x轴的交点为D，连接AC，在抛物线上是否存在点E、F(点E、F关于直线l对称,且E在点F左侧),使得以D、E、F 为顶点的三角形与△AOC相似，若存在，求出点E的坐标，若不存在，请说明理由.
26.(本题满分10分)
问题探究
(1)如图1,点A、B、C在直线l上,点P在直线l外,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是 cm;
(2)如图2,在▱ABCD中,连接AC,AD=AC,∠ADC=α,点E为边AB上一点,连接DE交AC于点G,过点D作∠EDH=α,DH交BA延长线于点H,求证:△ADH∽△CDG;
问题解决
(3)某地拟规划一个形如五边形ABCFD所示的露营基地，如图3是设计师绘制的缩略示意图,其中∠B=90°,AD∥BC,AD=BC=2AB=10cm,为考虑露营客人娱乐休闲的需求,将△ADE区域设立成烧烤区，其余区域设立成花卉观赏区，O是该基地的一个出口(O为BC边的中点)，O、E之间的距离为2cm.根据设计要求： DF⟂DE,DF=12DE, 且该露营基地(五边形ABCFD)的面积要尽可能的小，问能否达到该规划的设计要求?若能，请求该露营基地面积的最小值；若不能，请说明理由.
数学试卷参考答案及评分标准
一、选择题(共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的)
1. B 2. C 3. D 4. B 5. C 6. A 7. C 8. D
二、填空题(共5小题，每小题3分，计15分)
9. x₁ =0,x₂=-3 10.3π 11.8 12.-6
13.4 3 如图，连接AC，作△ABC的外接圆⊙O，易得四边形ABCD是菱形，由菱形性质可知△ABC是等边三角形，可得动点P一定在劣弧AC上，在BP上取EP=AP,连接AE.证明△AEB≌△APC可得EB=PC,由EP=AP、∠APB=60°可知△APE是等边三角形,进而可得PA+PC=EP+EB=BP,故当BP为⊙O的直径时,PA+PC的值最大,此时∠BAP=90°,∠PBA=30°,解直角三角形便可求解.
三、解答题(共13小题，计81分.解答应写出过程)
14.解:原式=1-4×32-4-23 ………………………………………(3分)
=1-23-4+23
=-3. ………………………………………………………………………………………(5分)
15.解:由 12x>2 得:x>4, ………………………………………(2分)
由x-1≥2x+12得,x≤-2,………………………………………………………………………(4分)
∴原不等组无解………………………………………………………………………………………(5分)
16.解:方程两边同时乘(x+3)(x-3),得x-3+x²-9=( x-1 ) ( x+3) , ……………………………(2分)
整理，得： x-3+x²-9=x²+2x-3,
解得x=-9,…………………………………………………………………………………………(4分)
检验当x=-9时,(x+3)(x-3)≠0,
∴原方程的解为x=-9…………………………………………………………………………………(5分)
17.解：如图，点P即为所求.
…………………………………(5分)
注：①答案中线条为实线或虚线均不扣分；②没有写出结论不扣分；③答案不唯一，其他作法正确也可.
18.解:∠BAC=90°.……………………………………………………………………………………………(1分)
理由:∵F是AC的中点,∴CF=FA,
又∵FE=DF,
∴四边形AECD是平行四边形,…………………………………………………………………………(2分)
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形AECD是矩形…………………………………………………………………………………(4分)
∵∠BAC=90°,D是BC的中点,
∴AD=CD,
∴四边形AECD是正方形……………………………………………………………………………(5分)
注：答案不唯一，其他解法正确可参照得分.
19.解:如图,过C作CD⊥OA于D,则∠ODC=90°,
∵四边形OABC是菱形,
∴OC=OA=4, ………………………………… (2分)
∵∠AOC=60°,
∴OD=OC⋅cs∠AOC=12OC=2,CD=OC⋅sin∠AOC=32OC=23.…(4分)
∴点C的坐标为(2,23 ). ………………(5分)
20.解: 114. ……………………………………………(1分)
(2)画树状图如下：
由树状图可知，共有16种等可能的结果，其中小敏和小文选择不同小组的结果有12种，
∴小敏和小文选择不同小组的概率为 1216=34. ⋯⋯⋯⋯⋯⋯⋯(5分)
注：①在(2)中如果求出的概率正确，但没有列表格或画树状图扣2分；求出概率正确，若列表或画树状
图后没有就结果作出说明不扣分；②在(2)中若运用枚举法直接列举出16种等可能结果，只要结果正
确，不扣分.
21.解:∵∠ABQ=∠CDQ=90°,∠AQB=∠CQD,
∴△ABQ∽△CDQ, ……………………………………(3分)
∴ABCD=BQDQ, 即 1.61=6+DQDQ,
∴DQ=10,
∴BQ=BD+DQ=16,
∴EQ=EB+BQ=37.5…………………………………………(4分)
在Rt△EPQ中, tanE=PQEQ,
∴PQ=37.5tan 38.8°≈37.5×0.80=30.
∴摩天轮的高PQ为30米.…………………………………………………(6分)
注：算出PQ=30，没有单位，没有答语不扣分.
22.解:(1)设第一季度销售A产品x袋,则销售B产品(2000-x)袋,
由题意得:(12-8)x+(20-15)(2000-x)=9200…………………………………………(2分)
解得:x=800,
∴小林家第一季度销售A产品800袋………………………………………………………(3分)
(2)小林家第二季度A种产品的销售量为a袋，则B种产品销售量为(3600-a)袋，
由题意得:w=(12-8)a+(20-15)(3600-a)
∴w与a之间的函数关系式w=-a+18000……………………………………………(6分)
∵-1<0,∴w随a的增大而减小,
由题意知,a≤1000,
∴当a=1000时, W最小=17000.
∴小林家销售这两种产品至少获得总利润17000元……………………(7分)
23.解：(1)补全条形统计图如图所示：
9,8.…………………………………………………………………………(3分)
5(件),
此次所抽取班级上交绘画作品的平均件数为8.05件.……………………………………(5分)
(3)1000×8.05=8050(件).
答:估计此次绘画比赛共征集到8050件绘画作品………………………………………………(7分)
注：①(2)中直接写出平均数扣1分，没有答语不扣分；②(3)中没有计算过程扣1分，没有答语不扣分；③(2)、(3)不带单位均不扣分.
24.(1)证明:如图,连接OE,
∵AC是⊙O的切线,∴OE⊥AC,
∵∠ACB=90°,∴AC⊥BC,∴OE∥BC, ………………………………………(1分)
∴∠OED=∠F,
∵OD=OE,
∴∠ODE=∠OED,……………………………………………………(2分)
∴∠BDE=∠F,
∴BD=BF.…………………………………………………………………(3分)
∵CF=2,tanF=CECF,
(2)解:如图,连接BE,
∵ ∠BDE=∠F,∴tan F=tan∠BDE=2,
∴CE=4……………………………………………………………………(4分)
∵BD是⊙O直径,∴∠BED=90°,∴BE⊥EF,
∵ ∠ACB=90°,∴∠ECF=∠BCE=90°,
∴∠CEF+∠BEC=∠CBE+∠BEC=90°,∴∠CEF=∠CBE,
∴△ECF∽△BCE, …………………………………(6分)
∴CECF=CBCE,
∴CE²=BC· CF.
∴BC=8……………………………………………………………………………………………(7分)
∴ BF=BC+CF=10,
∴BD=BF=10,
∴OD=12BD=5 即⊙O的半径为5……………………………………………………………………(8分)
25.解:(1)在y=-x²-2x+3中,令y=0,则-x²-2x+3=0,
解得. x₁=-3,x₂=1 ,
∴点A的坐标为(-3,0),点B的坐标为(1,0)…………………………………………………………(2分)
在y=-x²-2x+3中,令x=0,则y=3,
∴点C的坐标为(0,3).…………………………………………………………………………………(3分)
当点E在x轴上方时,设E的横坐标为n(n<-1),
分两种情况讨论：
(2)存在.
由 y=-x²-2x+3=-( x+1)²+4 知抛物线的对称轴l为x=-1，
∴点D的坐标为(-1,0).
∵ A( -3,0),C( 0,3),∴ OA=OC=3,
故△AOC是以AC为斜边的等腰直角三角形，
∴∠OAC=45°.
如图,设EF交l于点G,
∵点E、F关于直线l对称,∴DF=DE,
若△EDF∽△AOC,则∠EDF=90°,∠DEF=45°,
易得DG=EG.………………………………………………………(4分)
则
E₁G₁=-1-n,DG₁=E₁G₁=-1-n.
∴E₁( n,-1-n),
将其代入y=-x²-2x+3中,得. -1 -n=-n²-2n+3,
解得n1=-1-172,n2=-1+172(舍去),
∴E1-1-172-1+172. ………………………………………………………………………(6分)
当点E在x轴下方时,设E₂的横坐标为n(n<-1),则E₂G₂=-1-n,DG₂=E₂G₂=-1-n.
∴ E₂(n,1+n) ,
将其代入y=-x²-2x+3中，得 1+n=-n²-2n+3,
解得n1=-3-172,n2=-3+172(舍去),
∴E2-3-172-1-172.
综上，在抛物线上存在点E、F，使得以D、E、F为顶点的三角形与△AOC相似，点E的坐标为 E1-1-172-1+172,E2-3-172-1-172. ……………………(8分)
26.解:(1)5………………………………………………………………………………………………(1分)
(2)证明:在▱ABCD中,AD=AC,∠ADC=α,
∴AB∥CD,∠ACD=∠ADC=α,
∴∠DAH=∠ADC=α,
∴∠DAH=∠GCD, …………………………………………(2分)
∵∠ADC=∠EDH=α,
∴∠EDH-∠ADE=∠ADC-∠ADE,
∴∠ADH=∠CDG,……………………………………………………………………………………(4分)
∴△ADH∽△CDG…………………………………………………………………………………(5分)
(3)如图,连接CD,作FI⊥CD于点I,EG⊥AD于点G,OH⊥AD于点H,则∠DGE=∠DIF=90°,
∴S菱形ABCD=AB⋅BC=5×10=50.
由题意可知四边形ABCD是矩形，
故要使五边形ABCFD的面积最小，只需△CDF的面积最小.
∵四边形ABCD是矩形,∴DC=AB,∠ADC=90°,
∵ DF⊥DE,∴∠EDF=∠ADC=90°,
∴∠GDE=∠IDF,
∴△GDE∽△IDF,…………………………………………………………………………………(7分)
∴EGFI=DEDF=2,
∴EG=2FI………………………………………………………………………………………(8分)
∵ AD=2AB=10,∴ DC=AB=5,
易得四边形ABOH是正方形,∴OH=AB=5,
∵ EG+OE≥OH,OE=2,
∴2FI+2≥5,
∴FI≥32,
∴FI底'N=32, ………………………………………………………………………………(9分)
∴SCDFW=12CD⋅FI正水=12×5×32=3.75.
∴S五边形ABCFD最小=S矩形ABCD+S△CDF最小=50+3.75=53.75.
故能达到该规划的设计要求，该露营基地面积的最小值为53.75cm²……………………………(10分)商品
A产品
B产品
成本（元／袋）
8
15
售价（元／袋）
12
20