2024年安徽省宿州市砀山县中考二模数学试题

这是一份2024年安徽省宿州市砀山县中考二模数学试题，共10页。

1．你拿到的试卷满分为150分，考试时间为120分钟．
2．试卷包括“试题卷”和“答题卷”两部分，请务必在“答题卷”上答题，在“试题卷”上答题是无效的．
3．考试结束后，请将“试题卷”和“答题卷”一并交回．
一、选择题（本大题共10小题，每小题4分，满分40分）
1．2024的倒数是（ ）
A．B．2024C．D．
2．下列计算正确的是（ ）
A．B．C．D．
3．如图是某个几何体的左视图，这个几何体不可能是（ ）
A．B．C．D．
4．已知关于的不等式的解集是，则的取值范围在数轴上可表示为（ ）
A．B．C．D．
5．对于二次函数的图象，下列说法不正确的是（ ）
A．开口向上B．対称轴是直线
C．顶点坐标为D．当时，随的增大而增大
6．如图，四边形内接于圆，且AB、BC都是圆的内接正五边形的边，则的度数为（ ）
A．B．C．D．
7．吴老师准备了4张大小、形状、质地完全相同的卡片，正面依次书写“逢”“考”“必”“过”，把这4张卡片背面朝上洗匀．某同学从中随机抽取两张，则这两张卡片的正面汉字恰能组成“必过”的概率是（ ）
A．B．C．D．
8．如图，在中，，角平分线CD分AB为3：2两条线段，若，则BD的长度是（ ）
A．B．C．D．4
9．设函数，，当时，函数的最大值是，函数的最大值是，则（ ）
A．B．C．D．2
10．如图，AD是等边边BC上的高，在AD、AC上分别取一点E、F，使，连接BE、BF．若，设，则的最小值为（ ）
A．B．C．2D．3
二、填空题（本大题共4小题，每小题5分，满分20分）
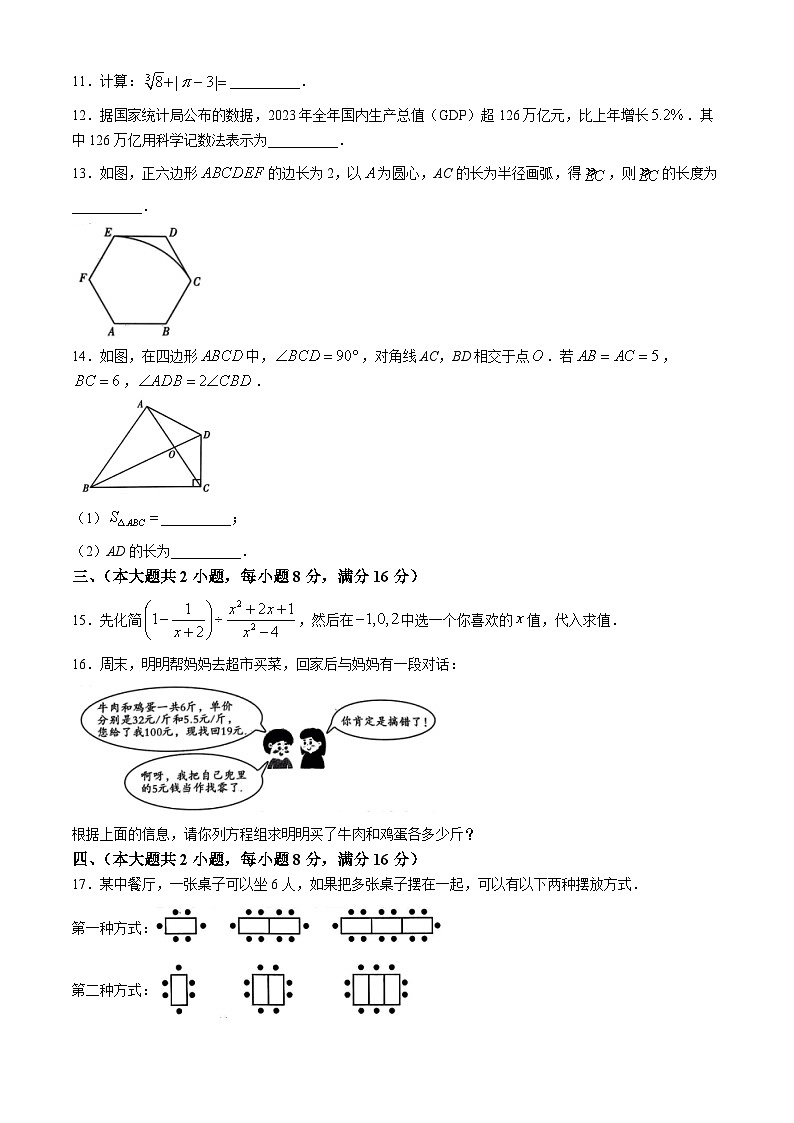
11．计算：__________．
12．据国家统计局公布的数据，2023年全年国内生产总值（GDP）超126万亿元，比上年增长．其中126万亿用科学记数法表示为__________．
13．如图，正六边形的边长为2，以为圆心，AC的长为半径画弧，得，则的长度为__________．
14．如图，在四边形中，，对角线AC，BD相交于点．若，，．
（1）__________；
（2）AD的长为__________．
三、（本大题共2小题，每小题8分，满分16分）
15．先化简，然后在中选一个你喜欢的值，代入求值．
16．周末，明明帮妈妈去超市买菜，回家后与妈妈有一段对话：
根据上面的信息，请你列方程组求明明买了牛肉和鸡蛋各多少斤？
四、（本大题共2小题，每小题8分，满分16分）
17．某中餐厅，一张桌子可以坐6人，如果把多张桌子摆在一起，可以有以下两种摆放方式．
第一种方式：
第二种方式：
（1）当有4张桌子时，第一种摆放方式能坐__________人，第二种摆放方式能坐__________人；
（2）当有n张桌子时，第一种摆放方式能坐__________人，第二种摆放方式能坐__________人；
（3）某天中午餐厅要接待一个70人的游客团队共同就餐（即桌子要摆在一起），但餐厅只有20张这样的餐桌．若你是这个餐厅的经理，你打算选择上述两种方式中的哪种来摆放餐桌？为什么？
18．如图，平面直角坐标系中，已知的三个顶点的坐标分别为，，．
（1）画出关于轴的对称图形；
（2）画出向左平移4个单位长度后得到的
（3）如果内部有一点经过上述两次变换，那么对应的点的坐标是多少？
五、（本大题共2小题，每小题10分，满分20分）
19，肥东县素有“吴楚要冲，包公故里”之美誉，县城境内的长江东路上，巍然屹立着一座神态威严的包公铜像，是这座城市珍贵而又显著的地标，一游客想知道包公铜像AB（含底座）的高度．如图，AB与水平面BD垂直，在点D处测得顶部A的仰角是37°，向前走了24米至点E处，测得此时顶部A的仰角是45°，请聪明的你帮游客求出包公铜像AB的高度．（参考数据：，，）
20．如图，在圆中，弦，垂足为，点为弧AC的中点，AB与弦DC、DM分别相交于点E、G．已知圆半径为4，．
（1）求证：；
（2）求FG的长．
六、（本题满分12分）
21．在学校组织的“青少年大学习”知识竞赛中，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，相应等级的得分依次记为100分，90分，80分，70分，学校将七年级（1）班和（2）班的成绩整理并绘制成如图所示的统计图：
请你根据以上提供的信息，解答下列问题：
（1）将表格补充完整：
（2）从平均数和中位数的角度对这次竞赛成绩的结果进行分析．
七、（本题满分12分）
22．如图1，矩形中，对角线AC的垂线DE交AC于点．
（1）求证：；
（2）若，求的值；
（3）延长DE与CB的延长线相交于点，连接AG，若，求证：．
八、（本题满分14分）
23．赛龙舟是我国传统的体育竞技项目，有着悠久的历史和广泛的群众基础．某龙舟队进行800米直道训练，全程分为启航，途中和冲刺三个阶段．图1，图2分别表示启航阶段和途中阶段龙舟划行总路程与时间的近似函数图象．启航阶段的函数表达式为；途中阶段匀速划行，函数图象为线段；冲刺阶段，龙舟先加速后匀速划行，加速期龙舟划行总路程与时间的函数表达式为．
（1）求出的值，并写出启航阶段自变量的取值范围；
（2）当时，求该龙舟划行的总路程；
（3）冲刺阶段，加速期龙舟用时1s将速度从提高到，之后保持匀速划行至终点．求该龙舟队完成训练总路程所需时间．
数学参考答案及评分标准
一、选择题（本大题共10小题，每小题4分，满分40分）
10．B
解析：如图1，作，垂足为，且，连接，．
是等边三角形，，，
，，，
，，，，
，共线时，的值最小．
如图2，同理当共线时，的值最小．
由，易得，所以，故选：B．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．12．13．
14．（1）12；（2）
解析：（1）如图，过点作于点，延长AD，BC交于点，则，
，，，，
；
（2），，，，
，，，
，，
，，，，，
解得．
三、解答题（本大题共2小题，每小题8分，满分16分）
15．解：原式，
当时，原式．
16．解：设明明买了牛肉斤，鸡蛋斤，
由题意得：，解得：，
答：明明买了牛肉2斤，鸡蛋4斤．
四、解答题（本大题共2小题，每小题8分，满分16分）
17．解：（1）当有4张桌子时，第一种摆放方式能坐人，第二种摆放方式能坐人，故答案为：18，12；
（2）第一种摆放方式，第一张桌子是6人，后边多一张桌子多4人．即有张桌子时是；
第二种摆放方式，第一张桌子是6人，后边多一张桌子多2人，即，
故答案为：，；
（3）打算用第一种摆放方式来摆放餐桌．
因为当时，第一种摆放方式：，第二种摆放方式：，
所以，选用第一种摆放方式．
18．解：（1）如图，即为所求；
（2）如图，即为所求；
（3）点经过上述两次变换，那么对应点的坐标为．
五、解答题（本大题共2小题，每小题10分，满分20分）
19．解：由题意得米，在中，，，，设米，在中，，，，解得，经检验是原方程的解，米，答：包公铜像AB的高度为72米．
20．解：（1）如图，连接BC，点为弧AC的中点，，，，，，
垂直平分CE，即；
（2）连接AD，由（1）同理可证得，，，，，，垂直平分，为AE中点，连接AC、OA、OC，
，为弧AC的中点，为等腰直角三角形，
半径为4，，．，
六、（本大题共12分）
21．解：（1）根据题意得：每班参加比赛的人数是（人），
七（1）班成绩的平均数：（分），
共有25人，中位数是第13个数，七（1）班成绩的中位数是90；
七（2）班100出现的次数最多，出现了（次），
七（2）班成绩的众数是100，
故答案为87．6，90，100；
（2）从平均数的角度看两班成绩一样；从中位数的角度看七（1）班比七（2）班的成绩好，所以七（1）班成绩更好．
七、（本大题共12分）
22．（1）：在矩形中，，，，
，即
（2）如图1，延长DE与CB的延长线相交于点，易得，
，，易证（或），
，，，点是线段AB的黄金分割点，
且BE为AE、AB的比例中项，；
（3）如图2，连接BD，
四边形是矩形，，，
又，，
又，四边形为平行四边形，
对角线AB与DG互相平分，，
再证Rt，，
即，．
八、（本大题共14分）
23．解：（1）把代入得，解得，
启航阶段总路程关于时间的函数表达式为；
（2）设，把代入，得，解得，．
当时，．当时，该龙舟划行的总路程为400m；
（3）由（1）可知，把代入，得．
函数表达式为，
把代入，解得．
，．
答：该龙舟队完成训练总程所需时间为．
成绩
班级
平均数
中位数
众数
七（1）班
__________
__________
90
七（2）班
87.6
80
__________
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
B
B
D
D
A
A
C
B