2025版高考数学一轮总复习知识梳理训练题第8章平面解析几何第6讲双曲线

这是一份2025版高考数学一轮总复习知识梳理训练题第8章平面解析几何第6讲双曲线，共4页。

知识点一 双曲线的定义
平面内与两个定点F1、F2的 距离的差的绝对值等于常数(小于|F1F2|) 的点的轨迹叫做双曲线．这两个定点叫做双曲线的 焦点 ，两焦点间的距离叫做双曲线的 焦距 .
注：设集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数，且a＞0，c＞0；
(1)当a＜c时，P点的轨迹是 双曲线 ；
(2)当a＝c时，P点的轨迹是 两条射线 ；
(3)当a＞c时，集合P是 空集 .
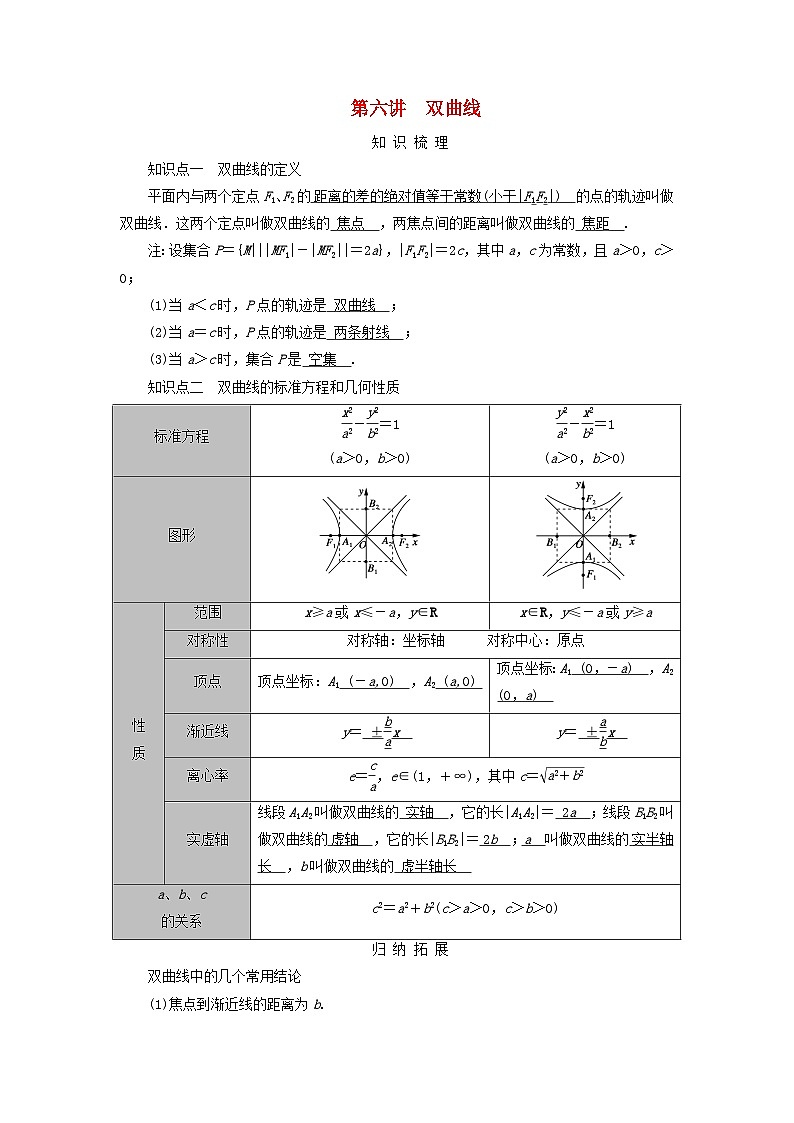
知识点二 双曲线的标准方程和几何性质
归 纳 拓 展
双曲线中的几个常用结论
(1)焦点到渐近线的距离为b.
(2)实轴长和虚轴长相等的双曲线叫做等轴双曲线．
双曲线为等轴双曲线⇔双曲线的离心率e＝eq \r(2)⇔双曲线的两条渐近线互相垂直(位置关系)．
(3)过双曲线的一个焦点且与实轴垂直的弦的长为eq \f(2b2,a)(通径)．
过双曲线的焦点与双曲线一支相交所得弦长的最小值为eq \f(2b2,a)；与两支相交所得弦长的最小值为2a.
(4)若P是双曲线右支上一点，F1，F2分别为双曲线的左、右焦点，则|PF1|min＝a＋c，|PF2|min＝c－a.过双曲线焦点F1的弦AB与双曲线交在同支上，则AB与另一个焦点F2构成的△ABF2的周长为4a＋2|AB|.
(5)双曲线的离心率公式可表示为e＝eq \r(1＋\f(b2,a2)).
(6)双曲线的形状与e的关系：|k|＝eq \f(b,a)＝eq \r(\f(c2,a2)－1)＝eq \r(e2－1)，e越大，即渐近线斜率的绝对值就越大，双曲线开口就越开阔．
(7)若M、N为双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)实轴端点，P为双曲线上不与M、N重合的点，则kPM·kPN＝eq \f(b2,a2).
(8)eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)与eq \f(y2,b2)－eq \f(x2,a2)＝1(a>0，b>0)互为共轭双曲线，其离心率倒数的平方和为1.
双 基 自 测
题组一 走出误区
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)平面内到点F1(0,4)，F2(0，－4)距离之差的绝对值等于8的点的轨迹是双曲线．( × )
(2)方程eq \f(x2,m)－eq \f(y2,n)＝1(mn>0)表示焦点在x轴上的双曲线．( × )
(3)双曲线方程eq \f(x2,m2)－eq \f(y2,n2)＝λ(m>0，n>0，λ≠0)的渐近线方程是eq \f(x2,m2)－eq \f(y2,n2)＝0，即eq \f(x,m)±eq \f(y,n)＝0.( √ )
(4)等轴双曲线的渐近线互相垂直，离心率等于eq \r(2).( √ )
(5)若双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)与eq \f(y2,b2)－eq \f(x2,a2)＝1(a>0，b>0)的离心率分别是e1，e2，则eq \f(1,e\\al(2,1))＋eq \f(1,e\\al(2,2))＝1(此条件中两条双曲线称为共轭双曲线)．( √ )
题组二 走进教材
2．(选择性必修1P127T8)与椭圆eq \f(x2,49)＋eq \f(y2,24)＝1有公共焦点，且离心率e＝eq \f(5,4)的双曲线的渐近线方程为 3x±4y＝0 .
[解析] 由题意知c＝eq \r(49－24)＝5，又e＝eq \f(c,a)＝eq \f(5,4)，∴a＝4，从而b＝eq \r(c2－a2)＝3.∴双曲线的渐近线方程为y＝±eq \f(3,4)x，即3x±4y＝0.
3．(多选题)(选择性必修1P146T11)已知常数a>0，点A(－a,0)，B(a,0)，动点M(不与A，B重合)满足：直线AM与直线BM的斜率之积为m(m≠0)，动点M的轨迹与点A，B共同构成曲线C，则关于曲线C的下列说法正确的是( BCD )
A．当m<0时，曲线C表示椭圆
B．当m<－1时，曲线C表示焦点在y轴上的椭圆
C．当m>0时，曲线C表示双曲线，其渐近线方程为y＝±eq \r(m)x
D．当m>－1且m≠0时，曲线C的离心率是eq \r(1＋m)
[解析] 设M(x，y)，则eq \f(y,x＋a)·eq \f(y,x－a)＝m，所以y2＝m(x2－a2)，即曲线C的方程为eq \f(x2,a2)－eq \f(y2,ma2)＝1，当m<0且m≠－1时，曲线C表示椭圆，A错误；当m<－1时，－ma2>a2，曲线C表示焦点在y轴上的椭圆，B正确；当m>0时，曲线C表示双曲线，其渐近线方程为y＝±eq \r(m)x，C正确；当m>0时，曲线C表示双曲线，其离心率为eq \r(1＋\f(ma2,a2))＝eq \r(1＋m)，当－1题组三 走向高考
4．(2021·全国新高考Ⅱ)已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的离心率为2，则该双曲线的渐近线方程为 y＝±eq \r(3)x .
[解析] 因为双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的离心率为2，
所以e＝eq \r(\f(c2,a2))＝eq \r(\f(a2＋b2,a2))＝2，所以eq \f(b2,a2)＝3，
所以该双曲线的渐近线方程为y＝±eq \f(b,a)x＝±eq \r(3)x.
故答案为y＝±eq \r(3)x.
5．(2023·新课标全国Ⅰ卷)已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左、右焦点分别为F1，F2.点A在C上，点B在y轴上，eq \(F1A,\s\up6(→))⊥eq \(F1B,\s\up6(→))，eq \(F2A,\s\up6(→))＝－eq \f(2,3)eq \(F2B,\s\up6(→))，则C的离心率为 eq \f(3\r(5),5) .
[解析] 解法一：依题意，设|AF2|＝2m，则|BF2|＝3m＝|BF1|，|AF1|＝2a＋2m，
在Rt△ABF1中，9m2＋(2a＋2m)2＝25m2，则(a＋3m)(a－m)＝0，
故a＝m或a＝－3m(舍去)，
所以|AF1|＝4a，|AF2|＝2a，|BF2|＝|BF1|＝3a，则|AB|＝5a，
故cs∠F1AF2＝eq \f(|AF1|,|AB|)＝eq \f(4a,5a)＝eq \f(4,5)，
所以在△AF1F2中，cs∠F1AF2＝eq \f(16a2＋4a2－4c2,2×4a×2a)＝eq \f(4,5)，整理得5c2＝9a2，故e＝eq \f(c,a)＝eq \f(3\r(5),5).
解法二：依题意，得F1(－c,0)，F2(c,0)，
令A(x0，y0)，B(0，t)，因为eq \(F2A,\s\up6(→))＝－eq \f(2,3)eq \(F2B,\s\up6(→))，
所以(x0－c，y0)＝－eq \f(2,3)(－c，t)，则x0＝eq \f(5,3)c，y0＝－eq \f(2,3)t，
又eq \(F1A,\s\up6(→))⊥eq \(F1B,\s\up6(→))，所以eq \(F1A,\s\up6(→))·eq \(F1B,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(8,3)c，－\f(2,3)t))(c，t)＝eq \f(8,3)c2－eq \f(2,3)t2＝0，
则t2＝4c2，又点A在C上，则eq \f(\f(25,9)c2,a2)－eq \f(\f(4,9)t2,b2)＝1，
整理得eq \f(25c2,9a2)－eq \f(4t2,9b2)＝1，则eq \f(25c2,9a2)－eq \f(16c2,9b2)＝1，
所以25c2b2－16c2a2＝9a2b2，
即25c2(c2－a2)－16a2c2＝9a2(c2－a2)，
整理得25c4－50a2c2＋9a4＝0，则(5c2－9a2)(5c2－a2)＝0，解得5c2＝9a2或5c2＝a2，
又e>1，所以e＝eq \f(3\r(5),5)或e＝eq \f(\r(5),5)(舍去)，故e＝eq \f(3\r(5),5).标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1
(a＞0，b＞0)
eq \f(y2,a2)－eq \f(x2,b2)＝1
(a＞0，b＞0)
图形
性
质
范围
x≥a或x≤－a，y∈R
x∈R，y≤－a或y≥a
对称性
对称轴：坐标轴 对称中心：原点
顶点
顶点坐标：A1 (－a,0) ，A2 (a,0)
顶点坐标：A1 (0，－a) ，A2 (0，a)
渐近线
y＝ ±eq \f(b,a)x
y＝ ±eq \f(a,b)x
离心率
e＝eq \f(c,a)，e∈(1，＋∞)，其中c＝eq \r(a2＋b2)
实虚轴
线段A1A2叫做双曲线的 实轴 ，它的长|A1A2|＝ 2a ；线段B1B2叫做双曲线的 虚轴 ，它的长|B1B2|＝ 2b ； a 叫做双曲线的 实半轴长 ，b叫做双曲线的 虚半轴长
a、b、c
的关系
c2＝a2＋b2(c＞a＞0，c＞b＞0)