


高教版(2021)基础模块上册1.3 集合的运算完美版ppt课件
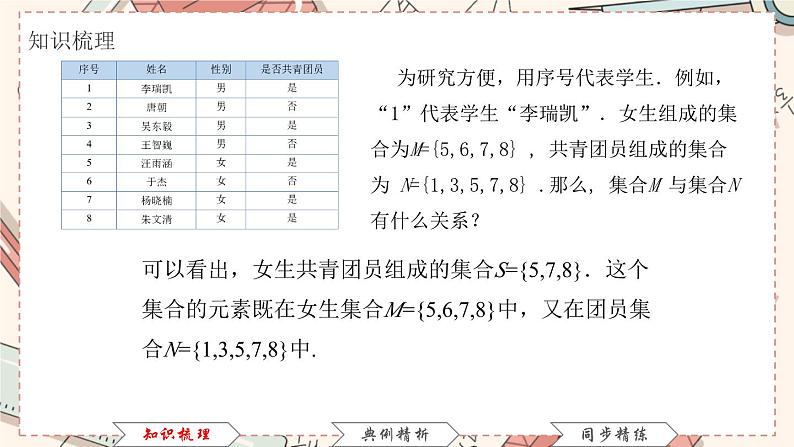
展开为研究方便,用序号代表学生.例如,“1”代表学生“李瑞凯”.女生组成的集合为M={5,6,7,8} , 共青团员组成的集合为 N={1,3,5,7,8} .那么, 集合M 与集合N 有什么关系?
可以看出,女生共青团员组成的集合S={5,7,8}.这个集合的元素既在女生集合M={5,6,7,8}中,又在团员集合N={1,3,5,7,8}中.
1.交集(1)交集的定义由属于集合A且属于集合B的所有元素组成的集合,称为集合A与集合B的交集.记作A∩B,读作A交B.即A∩B={x|x∈A且x∈B}.如图1-2中阴影部分.例如,A={1,2},B={1,3},则A∩B={1}.
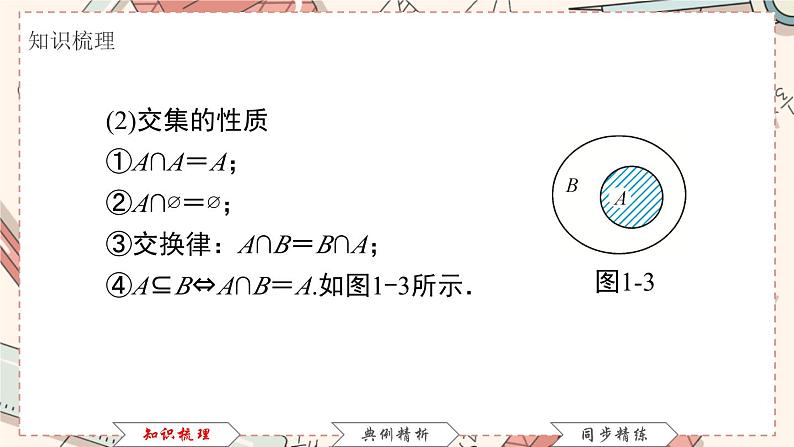
(2)交集的性质①A∩A=A;②A∩∅=∅;③交换律:A∩B=B∩A;④A⊆B⇔A∩B=A.如图1-3所示.
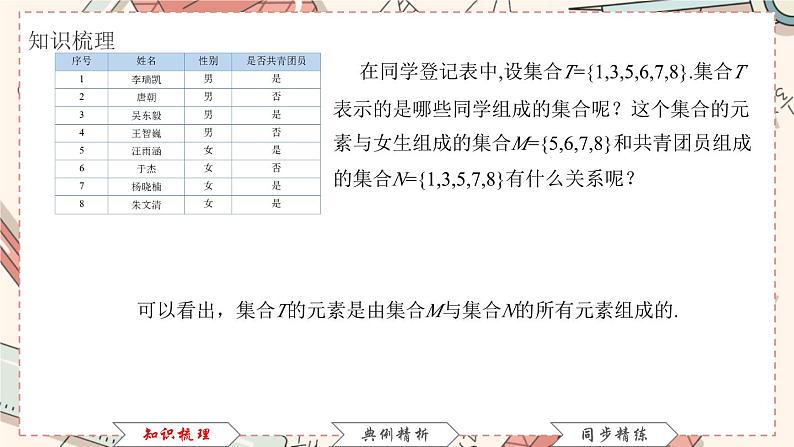
在同学登记表中,设集合T={1,3,5,6,7,8}.集合T表示的是哪些同学组成的集合呢?这个集合的元素与女生组成的集合M={5,6,7,8}和共青团员组成的集合N={1,3,5,7,8}有什么关系呢?
可以看出,集合T的元素是由集合M与集合N的所有元素组成的.
2.并集(1)并集的定义由属于集合A或属于集合B的所有元素组成的集合,称为集合A与集合B的并集.记作A∪B,读作A并B,即A∪B={x|x∈A或x∈B}.如图1-4中阴影部分.例如,A={1,2},B={1,3},则A∪B={1,2,3}.
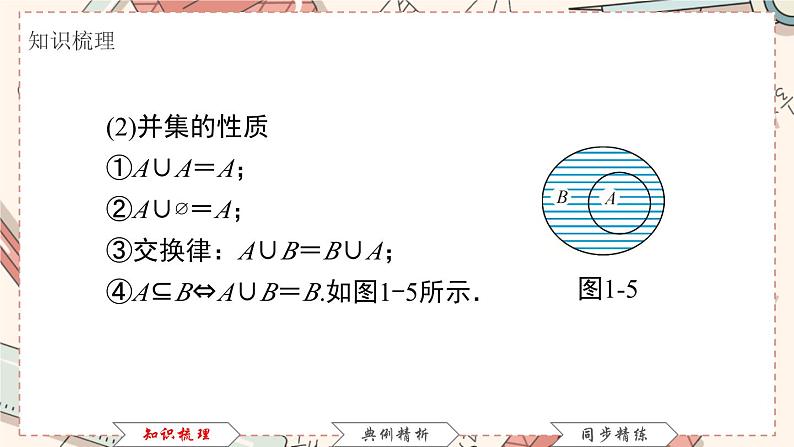
(2)并集的性质①A∪A=A;②A∪∅=A;③交换律:A∪B=B∪A;④A⊆B⇔A∪B=B.如图1-5所示.
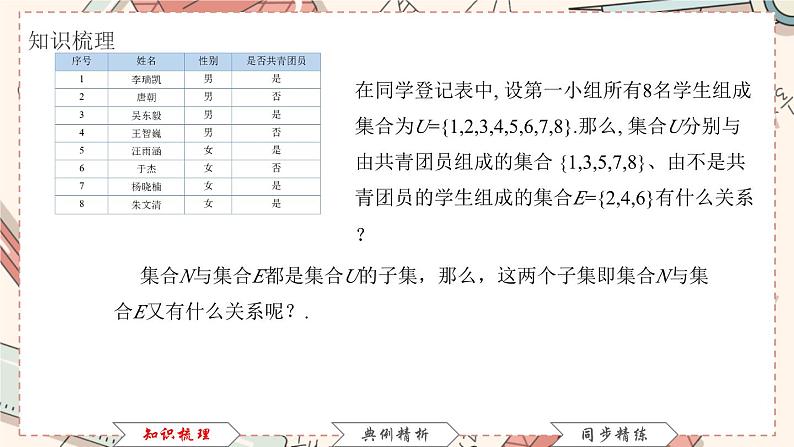
集合N与集合E都是集合U的子集,那么,这两个子集即集合N与集合E又有什么关系呢?.
在同学登记表中, 设第一小组所有8名学生组成集合为U={1,2,3,4,5,6,7,8}.那么, 集合U分别与由共青团员组成的集合 {1,3,5,7,8}、由不是共青团员的学生组成的集合E={2,4,6}有什么关系?
3.补集(1)全集的定义在研究集合之间的关系时,如果研究的集合都是一个给定集合的子集,那么这个给定集合称为这些研究集合的全集,通常记作U.例如,研究数的奇偶性时,是把整数集Z作为全集.
(2)补集的定义 如果集合A是全集U的一个子集,即A⊆U,由全集U中所有不属于A的元素构成的集合,称为集合A在全集U中的补集,记作∁UA,读作集合A在全集U中的补集,简称A的补集. 即∁UA={x|x∈U且x∉A}.如图1-6中阴影部分所示.
例如,U={1,2},A={1},则∁UA={2};又如,U=R,A={x|x≤0},则∁UA={x|x>0}.(3)补集的性质①A∩∁UA=∅;②A∪∁UA=U;③∁U(∁UA)=A.注意:若全集U=R,则U 通常省略不写,即∁UA=∁A.
【例1】 已知全集U={1,2,3,4,5},A={1,3},B={2,3,4}.求:(1)A∩B,A∪B,∁UA,∁UB;(2)∁U(A∩B),∁UA∪∁UB,∁U(A∪B),∁UA∩∁UB.(3)第(2)小题各个式子之间有什么等量关系?
【解析】 本题主要考查集合的运算.
答案 解:(1)A∩B={3},A∪B={1,2,3,4},∁UA={2,4,5},∁UB={1,5}.
(2)∁U(A∩B)={1,2,4,5},∁UA∪∁UB={1,2,4,5}, ∁U(A∪B)={5},∁UA∩∁UB={5}.
(3)∁U(A∩B)=∁UA∪∁UB;∁U(A∪B)=∁UA∩∁UB.
【变式训练1】已知全集U={1,2,3,4,5},A={1,4},B={3,4,5},C={1,2}.求:(1)A∩B,A∪B,∁UA,∁UB;(2)(A∩B)∩C,A∩(B∩C),(A∪B)∪C,A∪(B∪C).(3)第(2)小题各个式子之间有什么等量关系?
解:(1)A∩B={4},A∪B={1,3,4,5},∁UA={2,3,5}, ∁UB={1,2}.
(2)(A∩B)∩C={4}∩{1,2}=∅,A∩(B∩C)=A∩∅=∅,(A∪B)∪C={1,3,4,5}∪{1,2}={1,2,3,4,5},A∪(B∪C)={1,4}∪{1,2,3,4,5}={1,2,3,4,5}.
(3)(A∩B)∩C=A∩(B∩C),(A∪B)∪C=A∪(B∪C).
【例2】 已知全集U=R,A={x|1≤x<3},B={x|x<2},C={x|x>0}.求:(1)A∩B,A∪B,∁A,∁B;(2)A∩(B∪C),(A∩B)∪(A∩C).(3)第(2)小题各个式子之间有什么等量关系?
答案 解:(1)A∩B={x|1≤x<2},A∪B={x| x<3},∁A={x|x<1或x≥3},∁B={x|x≥2}.
【解析】 对于第(1)小题,按各自的定义在数轴上画图求解;对于第(2)小题,要注意运算顺序,有括号先算括号内的 .
(2)A∩(B∪C)={x|1≤x<3}∩R={x|1≤x<3},(A∩B)∪(A∩C)={x|1≤x<2}∪{x|1≤x<3}={x|1≤x<3}.(3)A∩(B∪C)=(A∩B)∪(A∩C).
【变式训练2】已知全集U=R,A={x|1≤x<4},B={x|x<3},C={x|x<0}.求:(1)A∩B,A∪B,∁A,∁B;(2)A∪(B∩C),(A∪B)∩(A∪C);(3)第(2)小题两个式子之间有什么等量关系?
解:(1)A∩B={x|1≤x<3},A∪B={x|x<4},∁A={x|x<1或x≥4},∁B={x|x≥3}.
(2)A∪(B∩C)={x|1≤x<4}∪{x|x<0}={x|x<0或1≤x<4},(A∪B)∩(A∪C)={x|x<4}∩{x|x<0或1≤x<4}={x|x<0或1≤x<4}.(3)A∪(B∩C)=(A∪B)∩(A∪C).
【例3】 已知A={(x,y)|x+3y=1},B={(x,y)|3x-y=3},求A∩B,并说明其几何意义.
【解析】 这里A∩B是指既满足x+3y=1,又满足3x-y=3的解集,即方程组 的解集. 由于二元一次方程的图形是直线,∴A∩B的几何意义是两直线的交点构成的集合.
答案 解:A∩B={(x,y)|x+3y=1}∩{(x,y)|3x-y=3}=这里A∩B的几何意义是两直线x+3y=1与3x-y=3的交点构成的集合.
【变式训练3】A={(x,y)|y=x},B={(x,y)|y=x2},求A∩B,并说明其几何意义.
解:A∩B={(x,y)|y=x}∩{(x,y)|y=x2}= 这里A∩B的几何意义是直线y=x与抛物线y=x2的交点构成的集合.
一、选择题1.已知集合A={1,2,3,4},B={3,4,5},则A∩B=( ) A.{1,2,3,4,5} B.{1,3,4} C.{2,3,4} D.{3,4}
【提示】 A∩B是指它们的公共元素组成的集合.故选D.
2.已知集合A={1,2,3,4},B={x|2
4.已知集合A={3,4},B={x|2
【提示】 {x|x2+9=0}∪{x|x2-9=0}=∅∪{-3,3}={-3,3}.故选C.
7.设全集U={1,2,3,4,5},已知A={1,3},B={2,3,4},则∁UA∩B=( ) A.{1,2,4,5} B.{2,4} C.{2,3,4} D.{3,4}
【提示】∁UA∩B={2,4,5}∩{2,3,4}={2,4}.故选B.
8.设全集U={1,2,3,4,5},已知A={1,3},B={2,3,4},则∁U(A∩B)=( ) A.{1,2,4,5} B.{2,4} C.{2,3,4} D.{3,4}
【提示】 ∁U(A∩B)=∁U{3}={1,2,4,5}.故选A.
9.若集合A={2,3,a},B={1,3},且A∩B={3},则a的值可能是( ) A.1 B.2C.3 D.4
【提示】 根据A∩B={3}及集合中元素的互异性,∴a的值可能是4.故选D.
10.已知集合M={1,3,4,5},N={2,3,4},则下列选项正确的是( ) A.M⊆N B.M⊇N C.M∪N={1,2,3,4} D.M∩N={3,4}
【提示】 ∵M={1,3,4,5},N={2,3,4},∴M和N都不是对方的子集,M∪N={1,2,3,4,5},M∩N={3,4}.故选D.
二、填空题11.{x|x=2n,n∈Z}∪{x|x=2n-1,n∈Z}=________.12.已知集合A={-1,0,1,2},B={x|x<1},则A∩B=____________.
【提示】 {x|x=2n,n∈Z}∪{x|x=2n-1,n∈Z}={偶数}∪{奇数}=Z.
【提示】 ∵A={-1,0,1,2},B={x|x<1},∴A∩B={-1,0}.
13.已知全集U=R,A={x|x2-2x-3=0},则∁ A= .14.{矩形}∩{菱形}=________.
【提示】 ∵A={x|x2-2x-3=0}={x|(x-3)(x+1)=0}={x|x=-1或x=3},∴∁A={x|x≠-1且x≠3}.
【提示】 既是菱形又是矩形的四边形是正方形.
{x|x≠-1且x≠3}
15.集合A含有11个元素,集合B含有7个元素,集合A∩B含有4个元素,则集合A∪B的元素个数为________.
【提示】 由集合的图示法可知,A∪B的元素个数为11+7-4=14.
三、解答题16.已知集合A={(x,y)|x+3y=0},B={(x,y)|3x-y=1},求A∩B,并说明其几何意义.
解:联立 解得∴A∩B=这里A∩B的几何意义是两直线x+3y=0与3x-y=1的交点构成的集合.
*17.已知集合M={x|x2+mx-6=0},N={x|x2-2x+n=0},且M∩N={2},求m和n的值及 M∪N.
解:∵M∩N={2},∴2∈M且2∈N.又∵M={x|x2+mx-6=0},N={x|x2-2x+n=0},∴ ∴
故M={x|x2+x-6=0}={x|(x+3)(x-2)=0}={-3,2},N={x|x2-2x=0}={x|x(x-2)=0}={0,2},∴M∪N={-3,0,2}.
中职数学高教版(2021)基础模块上册1.3 集合的运算精品ppt课件: 这是一份中职数学高教版(2021)基础模块上册<a href="/sx/tb_c4030579_t3/?tag_id=26" target="_blank">1.3 集合的运算精品ppt课件</a>,共39页。PPT课件主要包含了图1-2,图1-3,图1-4,图1-5,图1-6,变式训练1,变式训练2,变式训练3,选择题,解答题等内容,欢迎下载使用。
数学1.3 集合的运算评课课件ppt: 这是一份数学<a href="/sx/tb_c4030579_t3/?tag_id=26" target="_blank">1.3 集合的运算评课课件ppt</a>,共10页。
中职数学高教版(2021)基础模块上册第1章 集合1.3 集合的运算教学演示ppt课件: 这是一份中职数学高教版(2021)基础模块上册<a href="/sx/tb_c4030579_t3/?tag_id=26" target="_blank">第1章 集合1.3 集合的运算教学演示ppt课件</a>,共9页。












