

2023-2024学年河南省洛阳市洛宁县八年级(下)期中数学试卷(含解析)
展开1.下列各式:x23+1,5+yπ,a+ba−b,1n中,是分式的共有( )
A. 1个B. 2个C. 3个D. 4个
2.某种花粉的直径约为0.0000076米,则数据0.0000076用科学记数法表示为( )
A. 7.6×10−5B. 7.6×105C. 7.6×10−6D. 76×10−6
3.若把分式3xx+y中的x和y都扩大为原来的3倍,则分式的值( )
A. 不变B. 扩大为原来的9倍C. 扩大为原来的3倍D. 缩小为原来的13
4.若关于x的分式方程xx+4−1x+4=mx+4有增根,则m的值为( )
A. 1B. −4C. −5D. −3
5.某学校为进一步开展“阳光大课间”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4000元,购买篮球用了2800元,篮球的单价比足球贵16元.篮球和足球的单价分别是多少元?小明列出了方程2800x−40002x=16,则小明列的方程中x表示的是( )
A. 足球的单价B. 篮球的单价C. 足球的数量D. 篮球的数量
6.如图,一次函数y=ax+b与反比例函数y=kx(k>0)的图象交于点A(1,2),B(m,−1).则关于x的不等式ax+b>kx的解集是( )
A. x<−2或0
D. −1
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组2x−y=−m2x−y=−n的解的个数为( )
A. 0个B. 1个C. 2个D. 无数个
8.如图所示,在平行四边形中,EF过对角线的交点,若AB=4,BC=7,OE=3,则四边形EFDC的周长是( )
A. 14B. 11C. 17D. 10
9.如图,在▱ABCD中,∠A+∠C=70°,则∠B的度数为( )
A. 125°B. 135°C. 145°D. 155°
10.直线l1:y1=k1x+b与直线l2:y2=k2x+c在同一平面直角坐标系中的图象如图所示,根据图象进行以下探究:
①k2<0;②b+c<0;③当x>1时,y1>y2;④若k1=1,c=−1,则S△ABC=8,
其中正确结论的个数共有( )
A. 1个
B. 2个
C. 3个
D. 4个
二、填空题:本题共5小题,每小题3分,共15分。
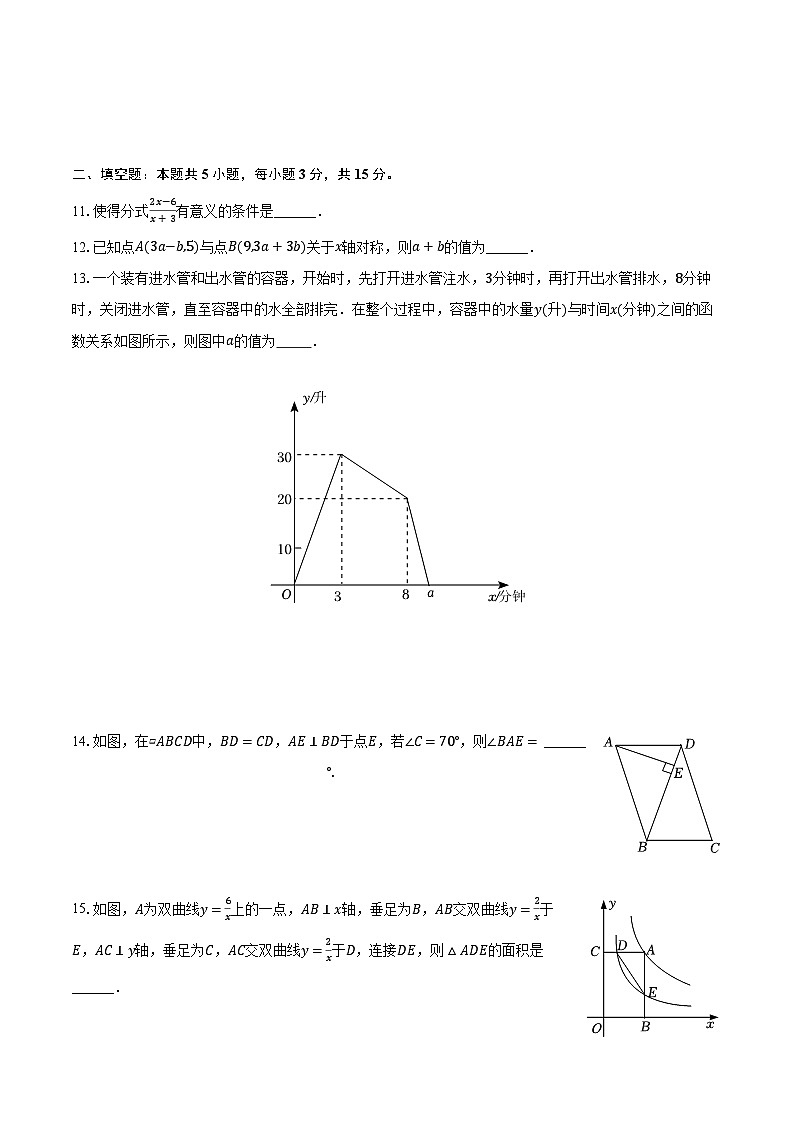
11.使得分式2x−6x+3有意义的条件是______.
12.已知点A(3a−b,5)与点B(9,3a+3b)关于x轴对称,则a+b的值为______.
13.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .
14.如图,在▱ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= ______°.
15.如图,A为双曲线y=6x上的一点,AB⊥x轴,垂足为B,AB交双曲线y=2x于E,AC⊥y轴,垂足为C,AC交双曲线y=2x于D,连接DE,则△ADE的面积是______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题8分)
计算:
(1)(3−π)0+(12)−3+(−1)2022;
(2)m−1m÷(m−1m).
17.(本小题8分)
先化简,再求值:a2−6a+9a2−2a÷(1−1a−2),其中a=4.
18.(本小题8分)
解方程:
(1)1x+1=4x−2;
(2)x+32x−6−xx−3=2.
19.(本小题10分)
随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
20.(本小题9分)
如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,求证:BM//DN.
21.(本小题10分)
如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.
22.(本小题11分)
教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后接通电源,则自动开始加热,每分钟水温上升10°C,待加热到100°C,饮水机自动停止加热,水温开始下降.水温y(°C)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20°C,接通电源后,水温y(°C)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40°C的开水,则他需要在什么时间段内接水?
23.(本小题11分)
如图,已知一次函数y=ax+b(a,b为常数,a≠0)的图象与x轴,y轴分别交于点A,B,且与反比例函数y=kx(k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于D,若OA=OD=34OB=3.
(1)求一次函数与反比例函数的解析式;
(2)观察图象直接写出不等式0
答案和解析
1.【答案】B
【解析】解:在x23+1,5+yπ,a+ba−b,1n中,是分式的:a+ba−b,1n,共2个.
故选:B.
判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
此题主要考查了分式定义,关键是掌握分式的分母必须含有字母,而分子可以含字母,也可以不含字母.
2.【答案】C
【解析】解:0.0000076=7.6×10−6,
故选:C.
将一个数表示成a×10n的形式,其中1≤|a|<10,n为常数,这种记数方法叫做科学记数法,据此即可求得答案.
本题考查科学记数法表示较小的数,科学记数法是基础且重要知识点,必须熟练掌握.
3.【答案】A
【解析】解:∵分式3xx+y中的x和y都扩大为原来的3倍,
∴3×3x3x+3y=9x3(x+y)=3xx+y.
故选:A.
先写出将分式3xx+y中的x和y都扩大为原来的3倍后的分式,再进行化简即可得出答案.
本题主要考查分式的基本性质,解题的关键是熟练掌握分式的基本性质.
4.【答案】C
【解析】解:将原分式方程化简得:x−1=m,
解得:x=1+m,
∵分式方程有增根,
∴x+4=0,
解得:x=−4,
∴1+m=−4,
解得:m=−5.
故选:C.
将原分式方程化成整式方程,令x+4=0,解得x=−4,然后代入化简后的方程即可.
本题主要考查了分式方程的增根,熟知分式方程的增根使得最简公分母等于0是解答本题的关键.
5.【答案】D
【解析】解:根据列出的方程,可知x表示篮球的数量,
故选:D.
根据方程2800x−40002x=16,即可确定x表示的量.
本题考查了由实际问题抽象出分式方程,理解给出的方程是解题的关键.
6.【答案】C
【解析】【分析】
本题主要考查了一次函数与反比例函数综合,正确求出点B的坐标是解题的关键.
先求出反比例函数解析式,进而求出点B的坐标,然后直接利用图象法求解即可.
【解答】
解:∵A(1,2)在反比例函数y=kx(k>0)的图象上,
∴k=1×2=2,
∴反比例函数解析式为y=2x,
∵B(m,−1)在反比例函数y=2x图象上,
∴m=2−1=−2,
∴B(−2,−1),
由题意得关于x的不等式ax+b>kx的解集即为一次函数图象在反比例函数图象上方时自变量的取值范围,
∴关于x的不等式ax+b>kx的解集为−2
故选:C.
7.【答案】A
【解析】【分析】
本题考查了一次函数与二元一次方程(组).
由图象可知,一次函数y1=2x+m与y2=2x+n(m≠n)是两条互相平行的直线,所以关于x与y的二元一次方程组2x−y=−m2x−y=−n无解.
【解答】
解:∵一次函数y1=2x+m与y2=2x+n(m≠n)是两条互相平行的直线,
∴关于x与y的二元一次方程组2x−y=−m2x−y=−n无解.
故选:A.
8.【答案】C
【解析】解:∵四边形ABCD为平行四边形,
∴OB=OD,AD//BC,AB=CD=4,
∴∠OBE=∠ODF,
在△BOE和△DOF中,∠OBE=∠ODFOB=OD∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴BE=DF,OE=OF=3,
∴CE+DF=CE+BE=BC=7,
∴四边形EFDC的周长=DF+EF+CE+CD=BC+OE+OF+CD=7+3+3+4=17,
故选:C.
证△BOE≌△DOF(ASA),可求得OE=OF=3,BE=DF,则可求得答案.
本题主要考查平行四边形的性质、全等三角形的判定与性质等知识,证得△BOE≌△DOF是解题的关键.
9.【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB//CD,
∵∠A+∠C=70°,
∴∠A=∠C=35°,
∴∠B=180°−∠A=145°.
故选:C.
由在平行四边形ABCD中,∠A+∠C=70°,即可求得∠A与∠C的度数,继而求得答案.
此题考查了平行四边形的性质.注意平行四边形的对角相等,邻角互补是解题的关键.
10.【答案】C
【解析】解:∵直线l2经过二、四象限,
∴k2<0,故①正确;
由题意可知b<0,c<0,
∴b+c<0,故②正确;
由图象可知,当x>1时,y1>y2,故③正确;
设y1=x+b,由题意得1+b=−2,解得b=−3,
∴y1=x−3,
当y1=0时,x=3,
故点B的坐标为(3,0);
设y2=k2x−1,由题意得k2−1=−2,解得k2=−1,
∴y2=−x−1,
当y2=0时,x=−1,
∴点A的坐标为(−1,0);
∴S△ABC=12×(3+1)×2=4,故④错误,
∴正确结论的个数共有3个.
故选:C.
①根据一次函数的性质判断即可;②根据b、c的范围判断即可;③根据两条直线的交点坐标判断即可;④分别求出点A、B的横坐标,再根据三角形的面积公式计算即可.
本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合,运用数形结合的思想解决此类问题.
11.【答案】x≠−3
【解析】解:由题意得:x+3≠0,
解得:x≠−3,
故答案为:x≠−3.
根据分式有意义的条件可得:x+3≠0,再解即可.
此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.
12.【答案】−53
【解析】解:∵点A(3a−b,5)与点B(9,3a+3b)关于x轴对称,
∴3a−b=93a+3b=−5,
解得a=116b=−72,
则a+b=116−72=−53.
故答案为:−53.
直接利用关于x轴对称点的性质得出a,b的值,进而得出答案.
本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.
13.【答案】293
【解析】【分析】
本题考查函数的图象,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
设出水管每分钟排水x升.由题意进水管每分钟进水10升,则有80−5x=20,求出x,再求出8分钟后的放水时间,可得结论.
【解答】
解:设出水管每分钟排水x升.
由题意进水管每分钟进水10升,
则有80−5x=20,
∴x=12,
∵8分钟后的放水时间=2012=53,8+53=293,
∴a=293,
故答案为:293.
14.【答案】50
【解析】解:在△DBC中,
∵BD=CD,∠C=70°,
∴∠DBC=∠C=70°,
又∵在▱ABCD中,AD//BC,
∴∠ADB=∠DBC=70°,∠BAD=∠C=70°,
又∵AE⊥BD,
∴∠DAE=90°−∠ADB=90°−70°=20°,
∴∠BAE=∠BAD−∠DAE=50°.
故答案为:50.
因为BD=CD,所以∠DBC=∠C=70°,又因为四边形ABCD是平行四边形,所以AD//BC,所以∠ADB=∠DBC=70°,因为AE⊥BD,所以在直角△AED中,由余角的性质可求∠DAE,即可求解.
此题主要考查了平行四边形的基本性质,以及等腰三角形的性质,难易程度适中.
15.【答案】43
【解析】解:设A(a,6a),则E(a,2a),D(a3,6a),
∴AD=a−a3=23a,AE=6a−2a=4a,
∴S△ADE=12×23a⋅4a=43,
故答案为:43.
设A(a,6a),求得D、E的坐标,进而求得AD、AE,最后根据三角形的面积公式求得结果.
本题主要考查了反比例函数的图象与性质,矩形的性质,三角形的面积,关键用A点的横坐标表示AD与AE.
16.【答案】解:(1)原式=1+8+1=10;
(2)m−1m÷(m−1m)=m−1m÷m2−1m
=m−1m×mm2−1
=m−1m×m(m+1)(m−)
=1m+1.
【解析】(1)先算零指数幂,负整数指数幂及乘方运算,再算加法即可;
(2)先对小括号里的分式进行通分计算;再按分式乘法法则计算即可.
本题考查了分式的混合运算和有理数加减混合运算,解题的关键是掌握实数运算、整式运算的顺序及相关运算法则.
17.【答案】解:原式=(a−3)2a(a−2)÷(a−2a−2−1a−2)
=(a−3)2a(a−2)÷a−3a−2
=(a−3)2a(a−2)⋅a−2a−3
=a−3a,
当a=4时,原式=4−34=14.
【解析】根据分式的混合运算法则把原式化简,把a的值代入计算即可.
本题考查的是分式的化简求值,掌握分式的混合运算法则是解题的关键.
18.【答案】解:(1)(1)1x+1=4x−2,
方程两边同时乘以最简公分母(x+1)(x−2),x−2=4(x+1),
解得:x=−2,
经检验,x=−2是原方程的解;
(2)x+32x−6−xx−3=2,
方程两边同时乘以最简公分母2(x−3),(x+3)−2x=4(x−3),
即x+3−2x=4x−12,
解得:x=3,
当x=3时,2(x−3)=0,
∴x=3是方程的增根,原方程无解.
【解析】(1)方程两边同时乘以最简公分母(x+1)(x−2),化为整式方程,进而解方程即可求解,最后要检验;
(2)方程两边同时乘以最简公分母2(x−3),化为整式方程,进而解方程即可求解,最后要检验.
本题考查了解分式方程,熟练掌握分式方程的解法是解题的关键.
19.【答案】解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x−200)元,由题意,得
80000x=80000(1−10%)x−200,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元;
(2)设今年新进A型车a辆,则B型车(60−a)辆,获利y元,由题意,得
y=(1800−1500)a+(2400−1800)(60−a),
y=−300a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60−a≤2a,
∴a≥20.
∵y=−300a+36000,
∴k=−300<0,
∴y随a的增大而减小.
∴a=20时,y有最大值
∴B型车的数量为:60−20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
【解析】本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,一次函数的解析式的运用,解答时由销售问题的数量关系求出一次函数的解析式是关键.
(1)设去年A型车每辆售价x元,则今年售价每辆为(x−200)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60−a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
20.【答案】证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AM=CN,∴OM=ON,
在△BOM和△DON中,OB=OD ∠BOM=∠DON OM=ON ,
∴△BOM≌△DON(SAS),
∴∠OBM=∠ODN,
∴BM//DN.
【解析】由平行四边形的性质得出OA=OC,OB=OD,再证出OM=ON,由SAS证明△BOM≌△DON,得出对应角相等∠OBM=∠ODN,再由内错角相等,两直线平行,即可得出结论.
本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的判定方法;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.
21.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴CD//AB,
∴∠AFN=∠CEM,
∵FN=EM,∠AFN=∠CEM,AF=CE,
∴△AFN≌△CEM(SAS).
(2)解:∵△AFN≌△CEM,
∴∠NAF=∠ECM,
∵∠CMF=∠CEM+∠ECM,
∴107°=72°+∠ECM,
∴∠ECM=35°,
∴∠NAF=35°.
【解析】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识.
(1)利用平行线的性质,根据SAS即可证明;
(2)利用全等三角形的性质可知∠NAF=∠ECM,求出∠ECM即可;
22.【答案】解:(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b,
得,b=208k1+b=100,
解得:k1=10b=20,
∴当0≤x≤8时,y=10x+20,
当8
得k2=800,
∴当8
解得x=40,
即a=40;
(3)当y=40时,x=80040=20,
∴要想喝到不低于40℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.
【解析】此题主要考查了反比例函数的应用,正确求出函数解析式是解题关键.
(1)直接利用反比例函数解析式和一次函数解析式求法得出答案;
(2)利用(1)中所求解析式,当y=20时,得出答案;
(3)当y=40时,代入反比例函数解析式,结合水温的变化得出答案.
23.【答案】解:(1)∵CD⊥OA,OA=34OB=3,
∴DC//OB,OB=4,
∴OBCD=OAAD=36=12,
∴CD=2OB=8,
∴A(3,0),B(0,4),C(−3,8),
把A、B两点的坐标分别代入y=ax+b可得3a+b=0b=4,解得a=−43b=4,
∴一次函数解析式为y=−43x+4,
∵反比例函数y=kx的图象经过点C,
∴k=−24,
∴反比例函数的解析式为y=−24x;
(2)解集为−3≤x<0;
(3)存在,满足条件的点P,其坐标为(0,−1)或(0,9)或(0,12).
【解析】(1)见答案;
(2)解:由题意可知所求不等式的解集即为直线AC在x轴上方且在反比例函数图象下方的图象所对应的自变量的取值范围,
即线段BC(包含C点,不包含B点)所对应的自变量x的取值范围,
∵C(−3,8),
∴0<−43x+4≤−24x的解集为−3≤x<0;
(3)解:∵B(0,4),C(−3,8),
∴BC=5,
∵△PBC是以BC为一腰的等腰三角形,
∴有BC=BP或BC=PC两种情况,
①当BC=BP时,即BP=5,
∴OP=BP+OB=4+5=9,或OP=BP−OB=5−4=1,
∴P点坐标为(0,9)或(0,−1);
②当BC=PC时,则点C在线段BP的垂直平分线上,
∴线段BP的中点坐标为(0,8),
∴P点坐标为(0,12);
综上可知存在满足条件的点P,其坐标为(0,−1)或(0,9)或(0,12).
本题为反比例函数的综合应用,涉及待定系数法、平行线分线段成比例、函数与不等式、等腰三角形的性质、数形结合及分类讨论思想等知识.在(1)中求得A、B、C的坐标是解题的关键,在(2)中注意利用数形结合思想,在(3)中确定出△PBC的两种情况是解题的关键.本题考查知识点较多,综合性较强.
(1)由平行线分线段成比例可求得CD的长,则可求得A、B、C的坐标,再利用待定系数法可求得函数解析式;
(2)由题意可知所求不等式的解集即为直线AC在x轴上方且在反比例函数图象下方的图象所对应的自变量的取值范围,结合函数图象可求得答案;
(3)由B、C的坐标可求得BC的长,当BC=BP时,则可求得P点坐标,当BC=PC时,可知点C在线段BP的垂直平分线上,则可求得BP的中点坐标,进而求得P点坐标.
2023-2024学年河南省洛阳市洛宁县七年级(下)期中数学试卷(含解析): 这是一份2023-2024学年河南省洛阳市洛宁县七年级(下)期中数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
河南省洛阳市洛宁县2022-2023学年八年级上学期期中考试数学试卷(含解析): 这是一份河南省洛阳市洛宁县2022-2023学年八年级上学期期中考试数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河南省洛阳市洛宁县2022-2023学年八年级上学期期中考试数学试卷(含解析): 这是一份河南省洛阳市洛宁县2022-2023学年八年级上学期期中考试数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












