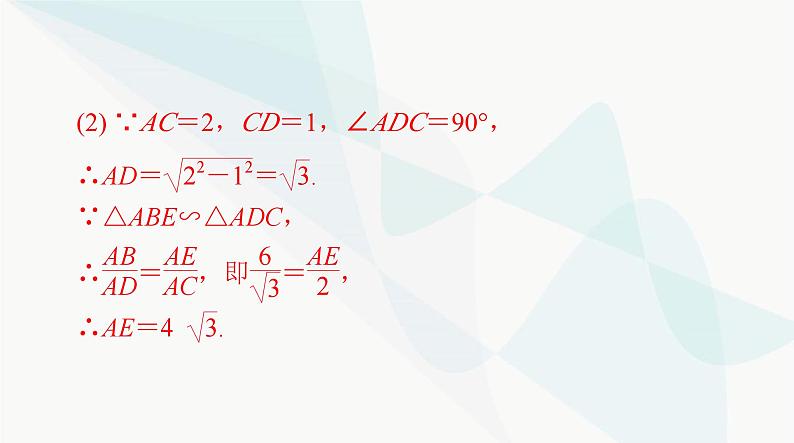
中考数学总复习第六章第二十四课时圆的有关性质课件

这是一份中考数学总复习第六章第二十四课时圆的有关性质课件，共35页。PPT课件主要包含了所对的弦，两条弧，垂径定理及其应用，1求圆的半径，是⊙O的直径，或弦心距，B25°，C20°，D10°，A30°等内容，欢迎下载使用。

1.了解圆及其有关概念，了解弧、弦、圆心角的关系(三量关
2.了解圆心角与圆周角的关系、直径所对的圆周角的特征.3.理解垂径定理，会用其进行有关的运算与证明.4.了解圆的内接四边形的性质——对角互补.
1.同圆或等圆中，若两条弧相等，那么这两条弧___________相等、所对的圆心角也相等，反之也成立.2.同弧所对的圆周角等于圆心角的________.3.垂直于弦的直径平分弦且平分弦所对的________.4.圆的内接四边形对角________.
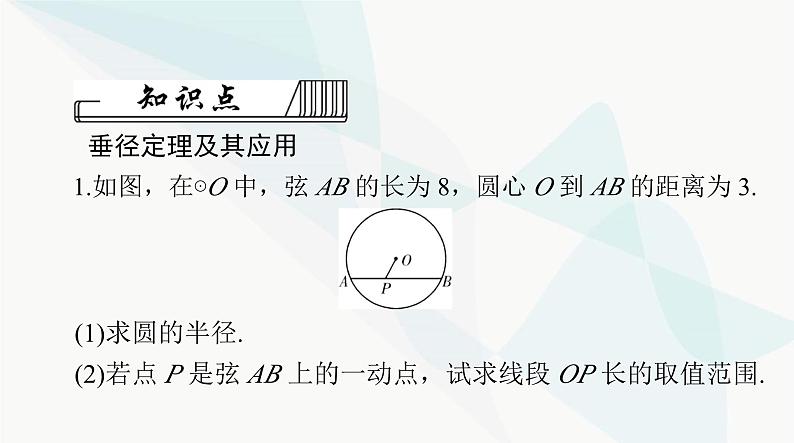
1.如图，在⊙O 中，弦 AB 的长为 8，圆心 O 到 AB 的距离为 3.
(2)若点 P 是弦 AB 上的一动点，试求线段 OP 长的取值范围.
解：(1)连接 OB，过点 O 作 OH⊥AB 于点 H(图略)，则 BH＝
(2)由题意知，当点 P 与点 H 重合时，OP 最短，当点 P 与点A 或点 B 重合时，OP 最长，∴3≤OP≤5.
圆周角定理及其推论的应用
2.如图，△ABC 的顶点都在⊙O 上，AD 是△ABC 的高，AE
(1)∠BAE 与∠CAD 相等吗？为什么？
(2)若 AC＝2，CD＝1，AB＝6，求 AE 的长.
解：(1)连接 BE(图略)，
∵AE 是直径，AD 是△ABC 的高，∴∠ABE＝∠ADC＝90°.
∵∠E 和∠C 对着同一条弧 AB，∴∠E＝∠C，
∴△ABE∽△ADC，∴∠BAE＝∠CAD.
(2) ∵AC＝2，CD＝1，∠ADC＝90°，
1.垂径定理一般都与勾股定理结合应用，常作的辅助线是半径
2.当题中有直径条件时，一般是作辅助线构成直径所对的圆周角，利用“直径所对的圆周角是直角”这个性质寻找解题的突破口.
1.(2022·聊城)如图所示，AB，CD 是⊙O 的弦，延长 AB，CD
2.(2021·广东)如图，AB 是⊙O 的直径，点C为圆上一点，AC＝3 ，∠ABC 的平分线交 AC 于点 D，CD＝1，则⊙O 的直径为
3.(2022·兰州)如图，△ABC 内接于⊙O，CD 是⊙O 的直径，
∠ACD＝40°，则∠B＝(
4.(2021·凉山州)点 P 是⊙O 内一点，过点 P 的最长弦的长为
10 cm，最短弦的长为 6 cm，则 OP 的长为(
B.4 cmD.6 cm
A.3 cmC.5 cm答案：B
5.(2022·泸州)如图所示，AB 是⊙O 的直径，OD 垂直弦 AC 于
点 D，DO 的延长线交⊙O 于点 E.若 AC＝4
6.(2023·宜昌)如图，OA，OB，OC 都是⊙O 的半径，AC，OB
交于点 D.若 AD＝CD＝8，OD＝6，则 BD 的长为(
7.(2021·宜昌)如图，C，D 是⊙O 上直径 AB 两侧的两点，设
∠ABC＝25°，则∠BDC＝(
8.(2022·柳州)如图，点 A，B，C 在⊙O 上，∠AOB＝60°，
则∠ACB 的度数是________°.
9.(2023·永州)如图，⊙O 是一个盛有水的容器的横截面，⊙O的半径为 10 cm，水的最深处到水面 AB 的距离为 4 cm，则水面AB 的宽度为________cm.
10.(2023·东营)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问：径几何？”转化为现在的数学语言表达就是：如图，CD 为⊙O 的直径，弦 AB⊥CD，垂足为 E，CE＝1寸，AB＝10 寸，则直径 CD 的长度为________寸.
11.(2022·自贡)一块圆形玻璃镜面碎成了几块，其中一块如图所示，测得弦 AB 长 20 厘米，弓形高 CD 为 2 厘米，则镜面半径为________厘米.
12.(2021·常德)如图，已知四边形ABCD是圆O的内接四边形，
∠BOD＝80°，则∠BCD＝________.
13.(2023·武汉)如图，OA，OB，OC 都是⊙O 的半径，∠ACB
(1)求证：∠AOB＝2∠BOC.
(2)若 AB＝4，BC＝ ，求⊙O 的半径.
(1)证明：∵∠AOB＝2∠ACB，
∠BOC＝2∠BAC，∠ACB＝2∠BAC，∴∠AOB＝2∠BOC.
(2)解：如图，过点 O 作半径 OD⊥AB 于点 E，
14.(2022·广东)如图，四边形 ABCD 内接于⊙O，AC 为⊙O 的
直径，∠ADB＝∠CDB.
(1)试判断△ABC 的形状，并给出证明.
解：(1)△ABC 是等腰直角三角形.证明：∵AC 为⊙O 的直径，∴∠ADC＝∠ABC＝90°.∵∠ADB＝∠CDB，
∴AB＝BC，∴AB＝BC.又∵∠ABC＝90°，
∴△ABC 是等腰直角三角形.
15.(2023·无锡)如图，AB 是⊙O 的直径，FD 与⊙O 相切于点D，CD 与 AB 相交于点 E.DF∥AB，DF 交 CA 的延长线于点 F，CF＝CD.
(1)求∠F 的度数.
(2)若 DE·DC＝8，求⊙O 的半径.
解：(1)如图，连接 OD.∵FD 为⊙O 的切线，∴∠ODF＝90°.∵DF∥AB，∴∠AOD＝180°－∠ODF＝90°.
(2)∵OA＝OD，∠AOD＝90°，∴∠EAD＝45°.∵∠ACD＝45°，∴∠ACD＝∠EAD.∵∠ADE＝∠CDA，∴△DAE∽△DCA.
∵OA2＋OD2＝2OA2＝DA2＝8，∴OA＝2，即⊙O 的半径为 2.
16.如图，射线 PG 平分∠EPF，O 为射线 PG 上一点，以 O为圆心，10 为半径作⊙O，分别与∠EPF 两边相交于点A，B和C，D，连接 OA，此时有 OA∥PE.
(1)求证：AP＝AO.
(3)若以图中已标明的点(即 P，A，B，C，D，O)构造四边形，
则能构成菱形的四个点为__________.
(1)证明：∵PG 平分∠EPF，∴∠DPO＝∠BPO.∵OA∥PE，
∴∠DPO＝∠POA ，∴∠BPO＝∠POA，∴AP＝AO.
∴PH＝2OH，设 OH＝x，