2022-2023学年湖南省衡阳市衡山县德华盛星源高级中学高二（下）期中数学试卷（含解析）

这是一份2022-2023学年湖南省衡阳市衡山县德华盛星源高级中学高二（下）期中数学试卷（含解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.某体育用品店有5款不同的篮球、4款不同的排球，某人要买一个篮球和一个排球，不同的选法有( )
A. 9种B. 10种C. 20种D. 36种
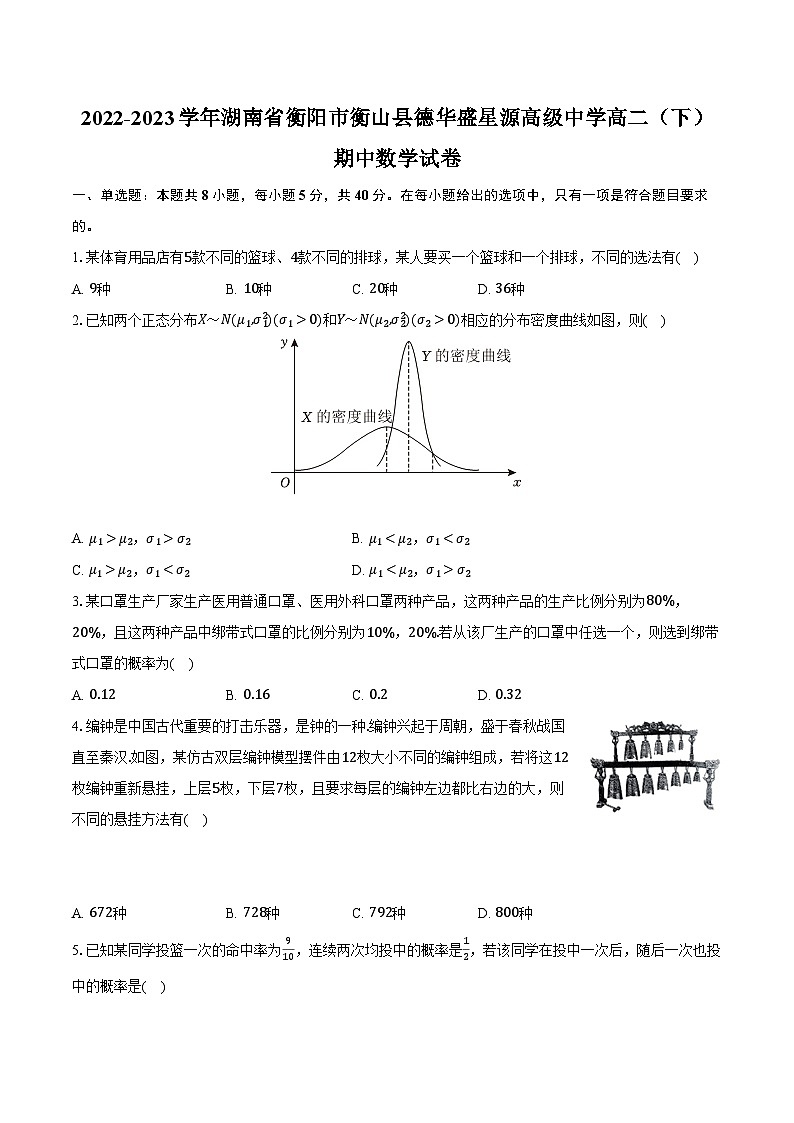
2.已知两个正态分布X～N(μ1,σ12)(σ1>0)和Y～N(μ2,σ22)(σ2>0)相应的分布密度曲线如图，则( )
A. μ1>μ2，σ1>σ2B. μ1<μ2，σ1<σ2
C. μ1>μ2，σ1<σ2D. μ1<μ2，σ1>σ2
3.某口罩生产厂家生产医用普通口罩、医用外科口罩两种产品，这两种产品的生产比例分别为80%，20%，且这两种产品中绑带式口罩的比例分别为10%，20%.若从该厂生产的口罩中任选一个，则选到绑带式口罩的概率为( )
A. 0.12B. 0.16C. 0.2D. 0.32
4.编钟是中国古代重要的打击乐器，是钟的一种.编钟兴起于周朝，盛于春秋战国直至秦汉.如图，某仿古双层编钟模型摆件由12枚大小不同的编钟组成，若将这12枚编钟重新悬挂，上层5枚，下层7枚，且要求每层的编钟左边都比右边的大，则不同的悬挂方法有( )
A. 672种B. 728种C. 792种D. 800种
5.已知某同学投篮一次的命中率为910，连续两次均投中的概率是12，若该同学在投中一次后，随后一次也投中的概率是( )
A. 15B. 25C. 35D. 59
6.一袋中装有编号分别为1，2，3，4的4个球，现从中随机取出2个球，用X表示取出球的最大编号，则E(X)=( )
A. 2B. 3C. 103D. 113
7.如图，在墙角有一根长1米的直木棒AB紧贴墙面，墙面与底面垂直.在t=0s时，木棒的端点A以0.1m/s的速度竖直向下匀速运动，端点B向右沿直线运动，则端点B在t=5s这一时刻的瞬时速度为( )
A. 330m/s
B. 530m/s
C. 310m/s
D. 510m/s
8.某五面体木块的直观图如图所示，现准备给其5个面涂色，每个面涂一种颜色，且相邻两个面(有公共棱的两个面)所涂颜色不能相同.若有6种不同颜色的颜料可供选择，则不同的涂色方案有( )
A. 600种B. 1080种C. 1200种D. 1560种
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。
9.由数字1，2，3，5组成一个没有重复数字的四位数，下列结论正确的是( )
A. 可以组成24个数B. 可以组成18个奇数
C. 可以组成10个偶数D. 可以组成18个比2000大的数
10.已知随机变量X的分布列为：
若E(X)=115，则( )
A. x=15B. y=25C. P(X≤2)=35D. D(X)=1425
11.将正整数排成如下所示的数阵，则( )
1 23 456 78910…
A. 第10行第1个数为46B. 第10行第10个数为56
C. 前10行所有数的和为1540D. 第10行所有数的和为505
12.已知定义在R上的奇函数f(x)满足当x>0时，f(x)=lnx+ax.若存在等差数列x1，x2，x3，x4(x1A. 32eB. ln(1+34e)C. 34eD. 1e
三、填空题：本题共4小题，每小题5分，共20分。
13.在(x+1x)6的展开式中，x4的系数为______．
14.已知三次函数f(x)的导函数为f′(x)，函数y=x⋅f′(x)的图象如图所示，则f(x)在x= ______处取得极大值，在x= ______处取得极小值．
15.已知甲每次投掷飞镖中靶的概率为0.6，若甲连续投掷飞镖n次，要使飞镖最少中靶一次的概率超过90%，至少需要投掷飞镖______次.(参考数据：lg2≈0.3)
16.有穷数列{an}共有k项，其满足an+1=an2nan+1，n∈[1,k−1]，n∈N+，若k的最大值为4，则a1= ______．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题10分)
第十四届全国人民代表大会第一次会议于2023年3月5日上午开幕，3月13日上午闭幕.某校为了解学生对新闻大事的关注度，在该校随机抽取了100名学生进行问卷调查，问卷成绩近似服从正态分布N(85,σ2)，且P(80≤ξ≤85)=0.4．
(1)估计成绩在90分以上的学生人数；
(2)若本次问卷调查的得分不低于80分，则认为该学生对新闻大事关注度极高，在该校随机抽取10名学生，记对新闻大事关注度极高的学生人数为X，求X的期望．
18.(本小题12分)
A，B，C，D，E这5个家庭的子女人数如下表所示：
(1)若从这些子女中随机选一人，已知选到的是女孩，求该女孩来自E家庭的概率；
(2)若从这5个家庭中任选3个家庭，记女孩比男孩多的家庭数为X，求X的分布列及期望．
19.(本小题12分)
现有7本不同的书准备分给甲、乙、丙三人．
(1)若甲、乙、丙三人中，一人得1本，一人得2本，一人得4本，则不同的分配方法有多少种？
(2)若甲、乙、丙三人中，一人得3本，另外两人每人得2本，则不同的分配方法有多少种？
20.(本小题12分)
已知数列{an}满足a1=0，an+1=a2(an+1)，an+1>an，且{an+2}为等比数列．
(1)求{an}的通项公式；
(2)设数列{n+2an+2}的前n项和为Tn，证明：Tn<4．
21.(本小题12分)
某商场为了吸引顾客，举办了投篮得优惠券活动，规则如下：若顾客连续投中三次，游戏过关，停止游戏，获得9元优惠券；若连续未投中两次，游戏失败，停止游戏，获得3元优惠券；若投篮六次仍未分出游戏过关或失败，也停止游戏，获得6元优惠券.顾客小明准备参与该活动，已知小明的投篮命中率为23．
(1)求小明投篮五次结束游戏的概率；
(2)记小明获得的优惠券金额为X，求X的分布列及期望．
22.(本小题12分)
已知函数f(x)=ln(x+1)+ax(a∈R)，g(x)=x3+sinx．
(1)讨论f(x)的单调性；
(2)若a=0，证明：f(x)≤g(x)．
答案和解析
1.【答案】C
【解析】解：由题意可知，不同的选法有5×4=20．
故选：C．
根据分步乘法计数原理求解．
本题主要考查了分步乘法计数原理，属于基础题．
2.【答案】D
【解析】解：由图象可得X的密度曲线的对称轴在Y的密度曲线的对称轴的左侧，
故μ1<μ2，
随机变量X对应的数据更离散，Y对应的数据更集中，所以σ1>σ2，
故选：D．
由正态曲线和均值、标准差的意义判断即可．
本题考查正正态分布的密度曲线，属于简单题．
3.【答案】A
【解析】解：从该厂生产的口罩中任选一个，则选到绑带式口罩的概率为0.8×0.1+0.2×0.2=0.12．
故选：A．
根据相互独立事件乘法公式列式计算即可．
本题考查相互独立事件的乘法公式，是基础题．
4.【答案】C
【解析】解：将这12枚编钟重新悬挂，上层5枚，下层7枚，且要求每层的编钟左边都比右边的大，则不同的悬挂方法有C125C77=792种．
故选：C．
根据排列组合的知识，求解即可．
本题考查排列组合的应用，属于基础题．
5.【答案】D
【解析】解：记第一次投中为事件A，第二次投中为事件B，
由题意得，P(A)=910，P(AB)=12，
则该同学在投中一次后，随后一次也投中的概率是P(B|A)=P(AB)P(A)=12910=59．
故选：D．
根据条件概率公式计算即可．
本题考查条件概率公式，是中档题．
6.【答案】C
【解析】解：由题意随机变量X所有可能取值为2，3，4．
且P(X=2)=1C42=16，P(X=3)=C21C42=13，P(X=4)=C31C42=12．
因此X的分布列为：
则E(X)=2×16+3×13+4×12=103．
故选：C．
由题意随机变量X所有可能取值为2，3，4，然后求出各自对应的概率，即可求出X的分布列，再计算期望即可．
本题主要考查离散型随机变量的期望，考查运算求解能力，属于基础题．
7.【答案】A
【解析】解：根据题意，设B运动的路程为s，则s2+(1−0.1t)2=1，变形可得s= 1−(1−0.1t)2= −0.01t2+0.2t，
其导数s′=1−0.1t 20t−t2，则有s′|x=5= 330，即端点B在t=5s这一时刻的瞬时速度为 330．
故选：A．
根据题意，设B运动的路程为s，求出s的表达式，再求出其导数，将t=5代入计算可得答案．
本题考查导数的计算和几何意义，注意求出s的解析式，属于基础题．
8.【答案】D
【解析】解：根据题意，先涂面PAB，有6种选择；再涂面PBC，有5种选择；再涂面ABCD，有4种选择，
若面PAD与面PBC所涂颜色不同，则面PAD有3种选择，面PCD有3种选择．
若面PAD与面PBC所涂颜色相同，则面PCD有4种选择．
故不同的涂色方法有6×5×4×(3×3+4)=1560种．
故选：D．
根据题意，结合五面体的几何结构，依次分析各个侧面的涂色方法数目，由分步计数原理计算可得答案．
本题考查排列组合的应用，涉及分步计数原理的应用，属于基础题．
9.【答案】ABD
【解析】解：对于A，可以组成A44=24个数，A正确；
对于B，若组成奇数，则个位数字有3种情况，剩下的位置任意排列，有3A33=18个奇数，B正确；
对于C，若组成偶数，则个位数字有1种情况，剩下的位置任意排列，有A33=6个偶数，C错误；
对于D，要求四位数比2000大，其千位数字可以为2、3、4，有3种情况，
剩下的位置任意排列，有3A33=18个符合题意的四位数，D正确．
故选：ABD．
根据题意，结合分步乘法计数原理，依次分析选项即可．
本题考查排列组合的应用，属于基础题．
10.【答案】BCD
【解析】解：根据题意可知，15+x+y=115×1+2x+3y=115，解得x=25y=25，故A错误，B正确；
P(X≤2)=P(X=1)+P(X=2)=15+25=35，故C正确；
D(X)=(1−115)2×15+(2−115)2×25+(3−115)2×25=1425，故D正确．
故选：BCD．
首先利用分布列建立方程组，进一步求出x和y的值，最后求出数学期望和方差，逐项判断即可．
本题考查离散型随机变量的应用，属于中档题．
11.【答案】ACD
【解析】解：设每一行的第一个数字构成数列{an}，
由题图an+1−an=n，则an−an−1=n−1，…，a2−a1=1，
且n>1，累加得an−a1=(n−1)+(n−2)+(n−3)+⋅⋅⋅+1，
所以an=n2−n+22，显然n=1也成立，所以a10=46，A正确；
所以第10行第10个数为46+9=55，B错误；
前10行所有数字的和为1+2+3+⋅⋅⋅+55=1540，C正确；
第10行所有数字的和为46+47+48+⋅⋅⋅+55=505，D正确．
故选：ACD．
由题设每一行的第一个数字构成数列{an}，则an+1−an=n，累加求数列通项，进而判断A、B；应用等差数列前n项和公式判断C、D．
本题主要考查了数列的递推式，考查了归纳推理，属于中档题．
12.【答案】ABC
【解析】解：因为x1+x4=x2+x3=0，2x3=x2+x4，所以x4=3x3，
因为f(x1)，f(x2)，f(x3)，f(x4)成等比数列，
所以f(x4)f(x3)=f(x3)f(x2)=−1，
则f(x3)+f(x4)=0，即f(x3)+f(3x3)=0(x3>0)，
所以方程f(x)+f(3x)=lnx+ax+ln(3x)+a3x=0有正实数解，整理得−4a=3xln(3x2)，
设g(x)=3xln(3x2)，则g′(x)=3ln(3x2)+6，
当x> 33e时，g′(x)>0，当0所以g(x)在( 33e,+∞)上单调递增，在(0, 33e)上单调递减，
所以g(x)min=g( 33e)=−2 3e，
所以−4a≥−2 3e，解得a≤ 32e，故A正确；
设h(x)=ln(1+x)−x，h′(x)=11+x−1=−x1+x，
当x∈(0,+∞)时，h′(x)<0，h(x)单调递减，
所以h(34e)=ln(1+34e)−34e1e> 32e，故D错误．
故选：ABC．
由等差数列与等比数列的性质可推出f(x3)+f(3x3)=0(x3>0)，则方程f(x)+f(3x)=lnx+ax+ln(3x)+a3x=0有正实数解，整理得−4a=3xln(3x2)，设g(x)=3xln(3x2)，利用导数可求出g(x)的最小值，从而可得a的取值范围，进而可得结论．
本题主要考查利用导数研究函数的最值，考查逻辑推理的核心素养，属于中档题．
13.【答案】6
【解析】解：在(x+1x)6的展开式中，通项公式为Tr+1=C6r⋅x6−2r，
令6−2r=4，可得r=1，故x4的系数为C61=6．
故答案为：6．
在二项式展开式的通项公式中，令x的幂指数等于4，求得r的值，可得x4的系数．
本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．
14.【答案】5 −5
【解析】解：当−50，
x<−5时，y=xf′(x)>0，可得f′(x)<0，
00，可得f′(x)>0，
x>5时，y=xf′(x)<0，可得f′(x)<0，
所以，f(x)在(−∞,−5)递减，在(−5,0)递增，在(0,5)递增，在(5,+∞)递减，
所以f(x)在x=−5处取得极小值，在x=5处取得极大值．
故答案为：5，−5．
结合所给的图象，讨论x<−5，−55，导数f′(x)的符号，可得f(x)的单调性，可得极值点．
本题考查导数的运用：求极值点，考查数形结合思想和推理能力，属于基础题．
15.【答案】3
【解析】解：甲每次投掷飞镖中靶的概率为0.6，若甲连续投掷飞镖n次，要使飞镖最少中靶一次的概率超过90%，
所以中靶0次的概率为(1−0.6)n，
所以1−(1−0.6)n>0.9，
两边取对数，nlg0.4故n>−2lg2≈2.5，
由于n∈N+，
故至少投掷3次．
故答案为：3．
直接利用独立重复试验和对立事件的关系建立1−(1−0.6)n>0.9，进一步利用对数的运算求出结果．
本题考查的知识要点：独立重复试验，对数的运算，主要考查学生的理解能力和计算能力，属于中档题．
16.【答案】−130
【解析】解：当an=0时，满足an+1=an2nan+1，此时k没有最大值，所以an≠0，
由an+1=an2nan+1，有1an+1=2nan+1an，即1an+1=2n+1an，可得1an+1−1an=2n，
则1an=(1an−1an−1)+(1an−1−1an−2)+⋯+(1a3−1a2)+(1a2−1a1)+1a1
=2n−1+2n−2+2n−3+⋯+22+2+1a1=2(1−2n−1)1−2+1a1=2n−2+1a1，
若k的最大值为4，则a5不存在，即1a5=25−2+1a1=0，
解得1a1=−30，即a1=−130．
故答案为：−130．
利用递推求数列{1an}的通项，由题意a5不存在，可知1a5=0，可求a1的值．
本题主要考查了数列的递推关系在数列项的求和中的应用，属于中档题．
17.【答案】解：(1)因为ξ～N(85,σ2)，P(80≤ξ≤85)=0.4，
所以P(ξ≥85)=0.5，P(85≤ξ≤90)=0.4，
所以P(ξ>90)=0.1，
即抽取学生中问卷成绩在90分以上的学生的概率为0.1，
所以抽取学生中问卷成绩在90分以上的学生的人数为100×0.1=10．
(2)由(1)P(80≤ξ≤85)+P(ξ>85)=0.9，
所以任意抽取一学生，该学生对新闻大事关注度极高的概率为0.9，
由已知X～B(10,0.9)，
所以X的分布列为：P(X=k)=C10k×(0.9)k×(0.1)10−k，k=0，1，2，…，10，
所以E(X)=10×0.9=9．
【解析】(1)结合正态分布密度曲线的对称性求出问卷成绩在90分以上的学生概率，由此可求问卷成绩在90分以上的学生人数；
(2)先求出问卷成绩在80分以上的学生概率，结合二项分布定义和期望公式求解即可．
本题考查离散型随机变量的期望，考查正态分布，是中档题．
18.【答案】解：(1)由题设，M表示选到女孩，Ni(i=A,B,C,D,E)表示选到对应家庭的孩子，
所以P(M)=47,P(M|NE)=23,P(NE)=37，
由P(M|NE)P(NE)=P(NE|M)P(M)，则P(NE|M)=P(M|NE)P(NE)P(M)=12，
所以选到的是女孩，该女孩来自E家庭的概率为12；
(2)由题意，5个家庭中任选3个家庭有{ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE}，
对应女孩比男孩多的家庭数为{1,0,1,1,2,1,1,2,1,2}，
所以X取值可能为{0,1,2}，且P(X=0)=110,P(X=1)=35,P(X=2)=310，
故X的分布列为：
所以E(X)=0×110+1×35+2×310=65．
【解析】(1)M表示选到女孩，Ni(i=A,B,C,D,E)表示选到对应家庭的孩子，应用贝叶斯公式求概率即可；
(2)列举出任选3个家庭的情况并写出对应女孩比男孩多的家庭数，即得X可能取值，进而求对应概率值，写出分布列并求期望．
本题考查了贝叶斯公式和离散型随机变量的分布列与期望，属于中档题．
19.【答案】解：(1)根据题意，分2步进分析：
①将7本书分为1−2−4的三组，有C71C62C44=105种分组方法，
②将分好的3组分给甲、乙、丙三人，有A33=6种情况，
则有105×6=630种分配方法；
(2)根据题意，分2步进分析：
①将7本书分为2−2−3的三组，有C72C52C33A22=105种分组方法，
②将分好的3组分给甲、乙、丙三人，有A33=6种情况，
则有105×6=630种分配方法．
【解析】(1)根据题意，分2步进分析：①将7本书分为1−2−4的三组，②将分好的3组分给甲、乙、丙三人，由分步计数原理计算可得答案；
(2)根据题意，分2步进分析：①将7本书分为2−2−3的三组，②将分好的3组分给甲、乙、丙三人，由分步计数原理计算可得答案．
本题考查排列组合的应用，涉及分步、分类计数原理的应用，属于基础题．
20.【答案】解：(1)因为an+1=a2(an+1)，
两边同加2得 an+1+2=a2(an+1)+2=a2an+a2+2，
因为{an+2}为等比数列，则an+1+2=q(an+2)=qan+2q，
则a2=qa2+2=2q，解得a2=2q=2，
此时a1+2=2，所以an+2=2×2n−1=2n，
所以an=2n−2，满足an+1>an．
(2)证明：n+22n−2+2=n+22n，
设Tn=1+221+2+222+⋯+n+12n−1+n+22n①，
12Tn=1+222+2+223+⋯+n+12n+n+22n+1②，
①−②得12Tn=32+122+123+⋯+12n−n+22n+1
=120+121+122+123+⋯+12n−n+22n+1
=1×[1−(12)n+1]1−12−n+22n+1=2−(12)n−n+22n+1，
所以Tn=4−(12)n−1−n+22n<4．
【解析】(1)构造出an+1+2=a2an+a2+2，结合等比数列定义得到关于a2，q的方程组，解出即可；
(2)利用乘公比错位相减法即可证明．
本题考查等比数列的定义和通项公式、求和公式，以及数列的错位相减法求和，考查方程思想和运算能力，属于中档题．
21.【答案】解：(1)若小明投篮五次后，游戏过关，
则五次投篮的情况依次为：投中，未投中，投中，投中，投中，
若小明投篮五次后，游戏失败，则五次投篮的情况依次为：投中，未投中，投中，未投中，未投中，
或未投中，投中，投中，未投中，未投中，
故所求概率为(23)2×(13)3×2+(23)4×13=881．
(2)根据活动规则，游戏过关的情况有4种，分别如下：
①连续投中三次；
②第一次未投中，之后连续投中三次；
③第一次投中，第二次未投中，之后连续投中三次；
④第一次投中或未投中，第二次投中，第三次未投中，之后连续投中三次；
其概率为(23)3+(23)3×13+(23)4×13×2=128243；
游戏失败的情况有7种，分别如下：
①连续未投中两次；
②第一次投中，之后连续未投中两次；
③第一次投中或未投中，第二次投中，之后连续未投中两次；
④第一次未投中，第二次及第三次投中，之后连续未投中两次；
⑤第一次投中，第二次未投中，第三次投中，之后连续未投中两次；
⑥第一次投中或未投中，第二次投中，第三次未投中，第四次投中，之后连续未投中两次；
⑦第一次投中，第二次未投中，第三次及第四次投中，之后连续未投中两次；
其概率为：(13)2+(13)2×23×2+(13)3×(23)2×3+(13)3×(23)3=233729，
投篮六次仍未分出游戏过关或失败的概率为：1−128243−233729=112729，
故X的分布列为：
E(X)=3×233729+6×112729+9×128243=1609243．
【解析】(1)分别考虑小明投篮五次后，游戏过关和不过关的情况，再由分类加法计数原理即可得出答案；
(2)求出X的可能取值，及对应的概率，即可得出分布列，再由期望公式求出E(X)．
本题考查离散型随机变量的分布列和期望，是中档题．
22.【答案】解：(1)f′(x)=ax+a+1x+1=1x+1+a，
当a≥0时，f′(x)>0，f(x)在(−1,+∞)上单调递增，
当a<0时，令ax+a+1x+1=0，得x=−1a−1>−1，
当−10，f(x)单调递增，
当−1a−1综上所述，当a≥0时，f(x)在(−1,+∞)上单调递增，
当a<0时，f(x)在(−1,−1a−1)上单调递增，在(−1a−1,+∞)上单调递减．
(2)证明：令h(x)=f(x)−g(x)=lnx−x3−sinx，
h′(x)=−3x3−3x2+1x+1−csx，
令u(x)=−3x3−3x2+1x+1−csx，
u′(x)=6x3+12x2+6x+1(x+1)2+sinx=−6x−1(x+1)2+sinx，
当−1t′(x)=6(3x2+4x+1)，
当−1当−13所以t(x)≥t(−13)=19>0，
所以6x3+12x2+6x+1(x+1)2>0，
又因为sinx≤0，
所以u′(x)<0，
当x>0时，令v(x)=6x+1(x+1)2，
v′(x)=6−2(x+1)2>0，
所以函数v(x)在(0,+∞)上单调递增，
v(x)>v(0)=1，即6x+1(x+1)2>1，
又因为sinx≤1，
所以u′(x)<0，
所以当x>−1时，u′(x)<0，u(x)在(−1,+∞)上单调递减，
又因为u(0)=0，
所以当−10，h(x)单调递增，
当x>0时，h′(x)<0，h(x)单调递减，
所以h(x)≤h(0)=0，
即f(x)≤g(x)．
【解析】(1)求导得f′(x)=1x+1+a，分两种情况：当a≥0时，当a<0时，分析f′(x)的符号，进而可得f(x)单调性，即可得出答案．
(2)令h(x)=f(x)−g(x)=lnx−x3−sinx，求导得h′(x)，分析h′(x)的符号，h(x)的单调性，最值，即可得出答案．
本题考查导数的综合应用，解题中需要理清思路，属于中档题．X
1
2
3
P
15
x
y
A
B
C
D
E
男孩
0
1
0
1
1
女孩
0
0
1
1
2
X
2
3
4
P
16
13
12
X
0
1
2
P
110
35
310
X
3
6
9
P
233729
112729
128243