



福建省厦门市杏南中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版)
展开考生注意:
1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,用0.5毫米黑色签字笔书写在答题卡相应位置上,超出答题区域的答案无效.写在本试卷上无效.
3.考试结束后,将答题卡交回.
一共、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
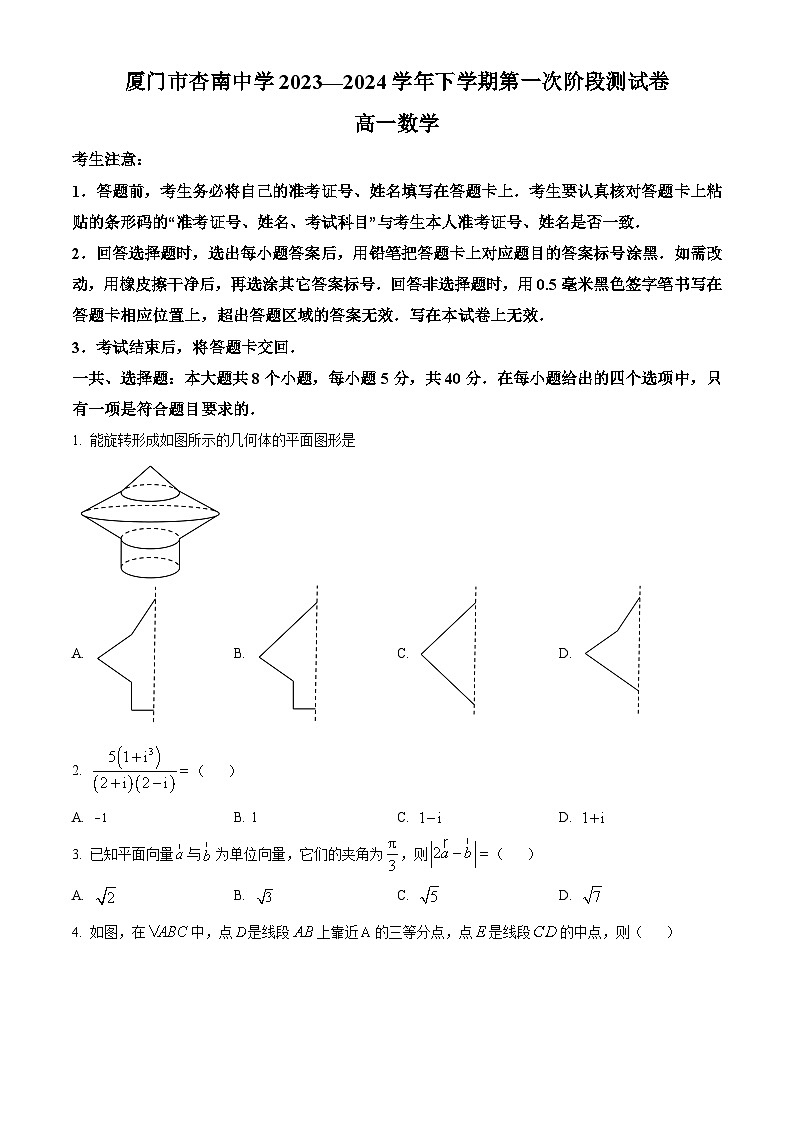
1. 能旋转形成如图所示的几何体的平面图形是
A. B. C. D.
【答案】A
【解析】
【分析】
将A、B、C、D选项图形绕对称轴旋转可知A选项符合题意.
【详解】此几何体自上向下是由一个圆锥、两个圆台和一个圆柱构成,
是由A中的平面图形旋转形成的.
故选:A.
【点睛】本题考查平面图形旋转形成的几何体,考查空间想象能力和推理能力,属于简单题.
2. ( )
A. B. 1C. D.
【答案】C
【解析】
【分析】利用复数的四则运算求解即可.
详解】
故选:C.
3. 已知平面向量与为单位向量,它们的夹角为,则( )
A. B. C. D.
【答案】B
【解析】
【分析】由向量模的公式转换为向量的数量积运算即可求解.
【详解】由题意.
故选:B.
4. 如图,在中,点是线段上靠近的三等分点,点是线段的中点,则( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据向量对应线段的位置关系,结合向量加法、数乘的几何意义,用表示即可.
【详解】由题图,.
故选:A
5. 已知向量的夹角为且|,,则在上投影向量的坐标为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据给定条件,利用投影向量的定义,结合向量坐标运算求解作答.
【详解】依题意,在上投影向量为,其中,
所以在上投影向量的坐标为.
故选:C
6. 在中,角所对的边分别为,向量,若,则角的大小为( )
A. B. C. D.
【答案】C
【解析】
【分析】先利用向量平行坐标运算得,再利用正弦定理结合两角和正弦公式进行边角转化,求解即可.
【详解】因为向量,且,所以,
由正弦定理可得:,
即,即,
又,,故,由,解得.
故选:C
7. 位于某海域A处的甲船获悉,在其正东方向相距20nmile的B处有一艘渔船遇险后抛锚等待营救,甲船立即前往救援,同时把消息告知位于甲船南偏西,且与甲船相距10nmile的C处的乙船.乙船也立即朝着渔船前往营救,则=( )
A. B. C. D.
【答案】A
【解析】
【分析】由余弦定理求得,进而由正弦定理求得答案.
【详解】
由题意,
由余弦定理得,,∴,
由正弦定理得,,即,解得.
故选:A.
8. 已知的三个角的对边分别为,且是边上的动点,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】
【分析】利用余弦定理计算先得,确定为直角三角形,再利用平面向量数量积公式结合二次函数的性质计算即可.
【详解】由余弦定理可知,
所以,即为直角三角形,.
设,则,
则,
显然时,.
故选:D
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列命题为真命题的是( )
A. 复数的虚部为
B. 若,则在复平面内对应的点的集合确定的图形面积为
C. 若为虚数单位,为正整数,则
D. 在复平面内,复数的共轭复数对应的点在第四象限
【答案】BC
【解析】
【分析】利用复数的定义,运算法则,几何意义一一判定选项即可.
【详解】由复数的概念可知复数的虚部为,故A错误;
若,则复平面内对应的点位于半径为1的圆上或内部,其面积为,故B正确;
根据复数的运算法则知,所以,故C正确;
易知复数的共轭复数为,其对应点为,显然位于第三象限,故D错误.
故选:BC
10. 已知向量,,则下列说法正确的是( )
A. 若,则B. 若,则
C. 的最小值为6D. 若与的夹角为锐角,则
【答案】BC
【解析】
【分析】由题意利用两个向量平行、垂直的性质,两个向量的数量积公式及向量模的坐标表示,逐一判断各个选项是否正确,从而得出结论.
【详解】解:向量,,
若,则,解得或,故A错误;
若,则向量,,由,所以,故B正确;
,,当且仅当时取等号,
故的最小值为6;故C正确;
若与的夹角为锐角,,且与不共线,
即,且,解得且,故D错误,
故选:BC.
11. 在中,角所对的边分别是,下列命题正确的是( )
A. 若,则为等腰三角形
B. 若,则此三角形有两解
C. 若,则等腰三角形
D. 若,且,则该三角形内切圆面积最大值是
【答案】ABD
【解析】
【分析】对于A,由可得,利用数量积的定义化为,从而得到,知为等腰三角形;对于B,由余弦定理可得到关于的方程,解得有两解,从而此三角形有两解;对于C,用正弦定理将条件化为,即,然后得到或,由此即可进一步判断;对于D,化简为,然后证明内切圆半径,从而得到.
【详解】对于A,若,则,从而,即,
即,故,从而为等腰三角形,A正确;
对于B,若,则,而,即,解得或,故此三角形有两解,B正确;
对于C,注意到等价于,而这又等价于,所以或,也就是为等腰三角形或直角三角形,C错误;
对于D,已知条件为,且,而等价于,即,
对该等式通分得到,即,即.
这即为,由知该等式即为.
从而条件等价于且,从而该三角形内切圆半径.
又由于,当且仅当时等号成立,
从而,故该三角形的内切圆面积.
验证知当时,等号成立,所以该三角形的内切圆面积的最大值是,D正确.
故选:ABD
【点睛】关键点点睛:D选项的关键是得出内切圆的半径,由此即可顺利得解.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知是关于的方程的一个根,则实数________
【答案】
【解析】
【分析】由题意可知方程两根分别为,,从而利用韦达定理即可得解.
【详解】因为是关于的方程的一个根,
所以也是方程的根,
所以,则.
故答案为:.
13. 在中,内角对应的边分别为,已知.则角________;若,则的值为________
【答案】 ①. #### ②.
【解析】
【分析】利用正弦定理计算可得第一空,利用余弦定理可得第二空.
【详解】(1)在中,由正弦定理得,
因为,所以,所以,
又因为,所以.
(2)在中,由余弦定理得,
代入数据解得,所以.
故答案为:;.
14. 在中,若,且AB边上的中线长为2,则面积的最大值为______
【答案】
【解析】
【分析】利用,可将结合正弦定理可得,后由余弦定理可得.后由结合AB边上的中线长为2,可得,后由基本不等式可得,即可得答案.
【详解】因,则
,
即.
所以,又,所以.设AB边上的中线为CD,
则,则,
所以,当且仅当a=b时等号成立,所以
故答案为:
四、解答题:共5题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知复数
(1)若z为纯虚数,求实数m的值:
(2)若z在复平面内对应的点在直线,求.
【答案】(1)
(2)答案见解析
【解析】
【分析】(1)根据纯虚数的概念列出方程或不等式,即可求得答案.
(2)根据题意列出m满足的方程,求得z,利用复数模的公式求得答案.
【小问1详解】
若纯虚数,则,解得.
【小问2详解】
由题意可得,解得或,
当时,,所以;
当时,,所以.
16. 已知为平面向量,且.
(1)若,且与垂直,求实数k的值;
(2)若,且,求向量的坐标.
【答案】(1)
(2)或
【解析】
【分析】(1)利用向量运算的坐标表示,向量垂直的坐标表示列出方程,求解作答.
(2)利用向量共线设出的坐标,利用坐标求模列式计算作答.
【小问1详解】
因为,则,
因为与垂直,于是,即,解得.
所以.
【小问2详解】
由,设,而,则,解得,
所以或.
17. 在中,角所对的边分别为,已知.
(1)求角的大小;
(2)若,求的面积.
【答案】(1)或
(2)或
【解析】
【分析】(1)根据正弦定理边角互化,结合特殊角的三角函数值求解即可;
(2)分类讨论,根据余弦定理求得,然后代入三角形面积公式求解即可.
【小问1详解】
由及正弦定理知:.
因为为三角形内角,则,所以.
因为为三角形内角,则或.
【小问2详解】
若,由余弦定理得,,
则,即,
即,因为,则,
所以的面积;
若,则,即,因为,则,
所以的面积.
18. 如图,在平行四边形中,分别是边的中点,与交于点,设.
(1)用表示;
(2)求的值;
(3)求的余弦值.
【答案】(1),
(2)
(3)
【解析】
【分析】(1)根据平面向量线性运算法则计算可得;
(2)首先求出,即,再根据数量积的运算律及定义计算可得;
(3)首先求出、,再由夹角公式计算可得。
【小问1详解】
根据题意,,
.
【小问2详解】
根据题意,由(1)可得, ,
在平行四边形中,,即为等边三角形,
所以,则,即,
则
.
【小问3详解】
因为,
,
故.
19. 在中,内角所对的边分别为,向量,且.
(1)求角的大小;
(2)若,
①求面积的最大值;
②求的取值范围.
【答案】(1)
(2)① ;②
【解析】
【分析】(1)根据即可得出,进行数量积的坐标运算即可得出,由正弦定理即可得出,根据余弦定理即可求出,从而求得;
(2)①首先得,进一步由余弦定理以及基本不等式得的最大值即可求解;②根据即可求出的外接圆直径为2,根据正弦定理即可得出,而,从而得出,从而求出的范围,即得出的范围.
【小问1详解】
;
;
由正弦定理得,;
;
,且;
;
【小问2详解】
①,
根据余弦定理得:,
即,
,
,
当且仅当时,等号成立,
所以,即面积的最大值为,
②;
外接圆直径;半径,
,
;
;
,
的取值范围是.
福建省永春第一中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版): 这是一份福建省永春第一中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版),文件包含福建省永春第一中学2023-2024学年高一下学期3月月考数学试题原卷版docx、福建省永春第一中学2023-2024学年高一下学期3月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
福建省泉州市晋江市养正中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版): 这是一份福建省泉州市晋江市养正中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版),文件包含福建省泉州市晋江市养正中学2023-2024学年高一下学期3月月考数学试题原卷版docx、福建省泉州市晋江市养正中学2023-2024学年高一下学期3月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
福建省泉州市惠南中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版): 这是一份福建省泉州市惠南中学2023-2024学年高一下学期3月月考数学试题(原卷版+解析版),文件包含精品解析福建省泉州市惠南中学2023-2024学年高一下学期3月月考数学试题原卷版docx、精品解析福建省泉州市惠南中学2023-2024学年高一下学期3月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。












