2022-2023学年福建省宁德市福安市八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年福建省宁德市福安市八年级（下）期中数学试卷（含解析），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是( )
A. B. C. D.
2.若x>y，则下列式子中错误的是( )
A. x+2>y+2B. x−1>y−1C. −2x>−2yD. x3>y3
3.因式分解结果为(2a+b)(2a−b)的多项式是( )
A. 4a2−b2B. 4a2+b2C. −4a2−b2D. −4a2+b2
4.如图，△ABC沿射线CB方向平移得到△DEF，点F在线段CB上，若BC=9cm，BF=5cm，则BE=( )
A. 3cm
B. 4cm
C. 5cm
D. 6cm
5.已知关于x的一元一次不等式的解集在数轴上表示如图所示，则这个不等式的解集是( )
A. x≤1B. x≥1C. x<1D. x>1
6.用反证法证明命题：“在△ABC中，∠A≠∠B，则AC≠BC”.应先假设( )
A. AC>BCB. AC7.已知△ABC，添加下列条件后能使△ABC为等边三角形的是( )
A. AB=ACB. ∠A+∠B=2∠C
C. AC2+BC2=AB2D. ∠A=∠B=60°
8.小红读一本300页的书，计划10天内读完，前5天因各种原因只读了100页，为了按计划读完，从第六天起平均每天至少要读多少页？设第六天起平均每天要读x页，根据题意列不等式是( )
A. 100+5x≥300B. 100+4x≥300C. 100+6x>300D. 100+5x>300
9.已知a−b=5，ab=−2，则a2b−ab2=( )
A. −50B. −10C. 10D. 20
10.如图，在△ABC中，点M，N为AC边上的两点，AM=NM，BM⊥AC，ND⊥BC于点D，且NM=ND，若∠A=α，则∠C=( )
A. 32α
B. 90°−12α
C. 120°−α
D. 2α−90°
二、填空题：本题共6小题，每小题3分，共18分。
11.如图，在Rt△ABC中，∠C=90°，∠A=40°，则∠B= ______°.
12.不等式组x+1>0x≤1的解集是______．
13.如图，在等腰三角形ABC中，AB=AC，BC=12，AD平分∠BAC，且AD=8，则AB的长是______．
14.因式分解：m2+2m+1= ______．
15.在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，△ABO的顶点在格点上，若△A′B′O′是由△ABO绕点P按逆时针方向旋转得到，且各顶点仍在格点上，则旋转中心P的坐标是______．
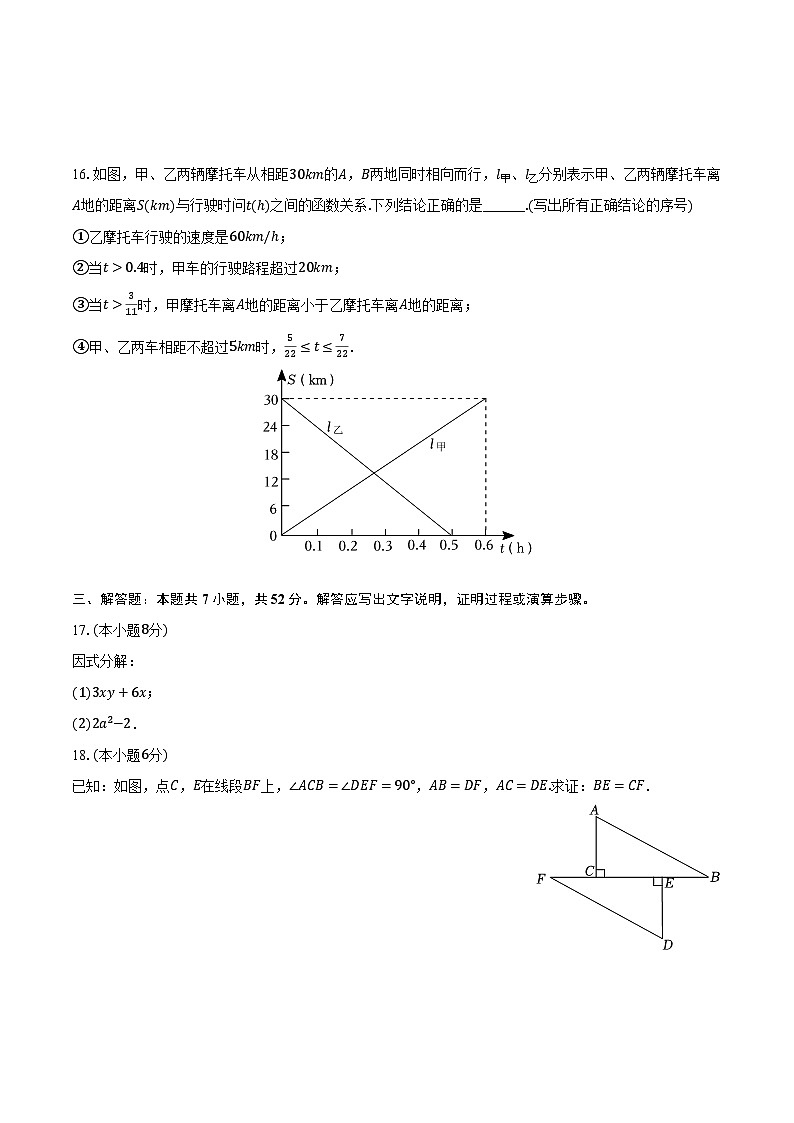
16.如图，甲、乙两辆摩托车从相距30km的A，B两地同时相向而行，l甲、l乙分别表示甲、乙两辆摩托车离A地的距离S(km)与行驶时问t(h)之间的函数关系.下列结论正确的是______.(写出所有正确结论的序号)
①乙摩托车行驶的速度是60km/h；
②当t>0.4时，甲车的行驶路程超过20km；
③当t>311时，甲摩托车离A地的距离小于乙摩托车离A地的距离；
④甲、乙两车相距不超过5km时，522≤t≤722．
三、解答题：本题共7小题，共52分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
因式分解：
(1)3xy+6x；
(2)2a2−2．
18.(本小题6分)
已知：如图，点C，E在线段BF上，∠ACB=∠DEF=90°，AB=DF，AC=DE.求证：BE=CF．
19.(本小题6分)
解不等式4(x−1)+3≤2x+5，并把它的解集在数轴上表示出来．
20.(本小题6分)
如图，都是由全等的边长为1的小等边三角形构成的网格，图中阴影部分是由若干个小等边三角形构成的，请分别按下列要求设计图案：

(1)在图1中画出将阴影部分图形沿某一方向平移3个单位长度后的图形，要求各顶点仍在格点上；
(2)在图2中再任意给两个小等边三角形涂上阴影，使得6个阴影小等边三角形组成的图形是中心对称图形；(只需画出符合条件的一种情形)
(3)在图3中画出将阴影部分图形绕点O按顺时针方向旋转60°后的图形．
21.(本小题7分)
如图，在△ABC中，AC=10．
(1)尺规作图：在BC边上确定一点D，使得AD⊥BC.(保留作图痕迹，不写作法)
(2)在(1)的条件下，若∠B=45°，∠C=30°，求BC的长．
22.(本小题9分)
某公司为庆祝第73个“五一”劳动节的到来，采购员计划向商家定制甲、乙两种水果礼盒共80个以慰问员工，其中甲、乙两种礼盒的单价分别为200元/个和350元/个，且两种礼盒的购买总金额不超过19000元．
(1)问甲种礼盒最少可以购买多少个？
(2)因该公司购买礼盒数量较多，经协商商家拟对该公司所够买的甲礼盒给予优惠a(25≤a≤30)元，已知甲、乙礼盒的成本分别为120元/个和290元/个，请求出商家获得的最大利润．
23.(本小题10分)
如图1，已知等腰三角形ABC与等腰三角形BED全等，边AB与边BE重合，BD交射线AC于点M，AB=AC．

(1)若∠ACB=72°，求∠AMB的度数．
(2)如图2，将等腰三角形BDE绕点B按顺时针方向旋转，过点E作EN//DB，交AM于点N．
①求证：EN=AN．
②判断EN，DM，CM的数量关系，并证明．
答案和解析
1.【答案】D
【解析】解：根据中心对称图形的定义，可知A，B，C选项不符合题意，D选项符合题意，
故选：D．
根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心，进行判断即可．
本题考查了中心对称图形，熟练掌握中心对称图形的定义是解题的关键．
2.【答案】C
【解析】解：A、若x>y，则x+2>y+2，故本选项变形正确；
B、若x>y，则x−1>y−1，故本选项变形正确；
C、若x>y，则−2x<−2y，故本选项变形错误；
D、若x>y，则x3>y3，故本选项变形正确；
故选：C．
根据不等式的性质逐项判断即得答案．
本题考查了不等式的性质，不等式两边都加上(或减去)同一个数或整式，不等号的方向不变；不等式两边都乘以或除以同一个正数，不等号的方向不变；不等式两边都乘以或除以同一个负数，不等号的方向改变；熟练掌握不等式的性质是关键．
3.【答案】A
【解析】解：(2a+b)(2a−b)=4a2−b2，
故选：A．
根据平方差公式：(a+b)(a−b)=a2−b2展开即可．
本题考查运用平方差公式进行因式分解，掌握平方差公式的形式是解题的关键．
4.【答案】B
【解析】解：∵△ABC沿射线CB方向平移得到△DEF，BC=9cm
∴BC=EF=9cm
∵BF=5cm，
∴BE=EF−BF=4cm，
故选：B．
根据平移的性质可得BC=EF=9cm即可求出BE的长度．
本题考查平移的性质，理解平移的对应线段相等是解题的关键．
5.【答案】C
【解析】解：由数轴知，这个不等式可以是：x<1，
故选：C．
在数轴上找不等式的解集可直接得出结论．
本题考查的是解一元一次不等式，根据数轴得到不等式的解集是解答此题的关键．
6.【答案】D
【解析】解：反证法证明命题：“在△ABC中，∠A≠∠B，则AC≠BC”，
先假设AC=BC．
故选：D．
根据反证法的步骤中，第一步是假设结论不成立，反面成立解答即可．
本题考查的是反证法的应用，解此题关键要懂得反证法的意义及步骤，在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
7.【答案】D
【解析】解：A.若AB=AC，则△ABC为等腰三角形，不一定是等边三角形，故本选项不符合题意；
B.若∠A+∠B=2∠C，则有∠A+∠B+∠C=3∠C=180°，解得∠C=60°，不能判断△ABC为等边三角形，故本选项不符合题意；
C.若AC2+BC2=AB2，则△ABC为直角三角形，不是等边三角形，故本选项不符合题意；
D.若∠A=∠B=60°，则根据“两个内角为60°的三角形是等边三角形”即可判断△ABC为等边三角形，符合题意．
故选：D．
由等腰三角形和等边三角形的关系、三角形内角和定理、勾股定理的逆定理以及等边三角形的判定定理即可获得答案．
本题主要考查了等腰三角形、等边三角形的判定、勾股定理的逆定理以及三角形内角和定理等知识，熟练掌握相关知识是解题关键．
8.【答案】A
【解析】解：根据题意得：100+5x≥300．
故选：A．
利用100页+后5天读的页数≥300页，即可列出关于x的一元一次不等式，此题得解．
本题考查了由实际问题抽象出一元一次不等式，根据各数量之间的关系，正确列出一元一次不等式是解题的关键．
9.【答案】B
【解析】解：∵a−b=5，ab=−2，
∴a2b−ab2=ab(a−b)=(−2)×5=−10，
故选：B．
把a2b−ab2化简，再整体代入求值即可．
本题考查因式分解的应用，解题的关键是利用整体思想代入求值．
10.【答案】D
【解析】解：∵AM=NM，BM⊥AC，∠A=α，
∴∠ABM=∠NBM=90°−α，
∵NM=ND，BM⊥AC，ND⊥BC，
∴BN平分∠NDM，
∴∠ABM=∠DBN=∠NBM=90°−α，
∴∠ABC=∠ABM+∠DBN+∠NBM=270°−3α，
∴∠C=2α−90°，
故选：D．
根据看垂直平分线的性质可得∠ABM=∠NBM=90°−α，NM=ND和BM⊥AC，ND⊥BC可得BN平分∠NDM，进而得到∠ABM=∠DBN=∠NBM=90°−α，最后由三角形内角和求出∠C即可．
本题考查垂直平分线的性质，角平分线的判定定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
11.【答案】50
【解析】解：∵在Rt△ABC中，∠C=90°，∠A=40°，
∴∠B=90°−∠A=90°−40°=50°．
故答案为50．
根据直角三角形两锐角互余即可求解．
本题考查了直角三角形的性质，掌握在直角三角形中，两个锐角互余是解题的关键．
12.【答案】−1【解析】解：x+1>0①x≤1②，
解不等式①得：x>−1，
解不等式②得：x≤1，
∴不等式组的解集为−1故答案为：−1先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可．
本题考查了解一元一次不等式组的应用，解此题的关键是能根据不等式的解集找出不等式组的解集，难度适中．
13.【答案】10
【解析】解：∵AB=AC，BC=12，AD平分∠BAC，AD=8，
∴AD⊥BC，BD=12BC=6，
∴在Rt△ABD中，可有AD2+BD2=AB2，
∴AB= AD2+BD2= 82+62=10．
故答案为：10．
由等腰三角形“三线合一”的性质可得AD⊥BC，BD=12BC=6，再在Rt△ABD中，由勾股定理即可获得答案．
本题主要考查了等腰三角形“三线合一”的性质以及勾股定理的应用，理解并掌握等腰三角形的性质是解题关键．
14.【答案】(m+1)2
【解析】解：原式=m2+2m+12=(m+1)2，
故答案为：(m+1)2．
根据完全平方公式分解即可．
本题主要考查了因式分解，理解完全平方公式的形式是解题的关键．
15.【答案】(2,0)
【解析】解：作AA′，OO′的垂直平分线，两线的交点即为旋转中心P，坐标为(2,0)；
故答案为：(2,0)．
根据旋转的性质：对应点到旋转中心的距离相等，即旋转中心在对应点连线的垂直平分线上，据此解答．
本题考查了旋转的性质，熟知对应点到旋转中心的距离相等是解题的关键．
16.【答案】①②④
【解析】解：由图可得，甲摩托车行驶的速度是30÷0.6=50km/h，
乙摩托车行驶的速度是30÷0.5=60km/h，故①正确；
当t=0.4时，甲车的行驶路程超过50×0.4=20km，故②正确；
当t=311时，甲摩托车离A地的距离311×50=15011，乙摩托车离A地的距离30−311×60=15011，
即甲摩托车离A地的距离等于乙摩托车离A地的距离；
由图可得，当t>311时，甲摩托车离A地的距离大于乙摩托车离A地的距离；故③错误；
设t小时时甲、乙两车相距为5km，则|30−60t−50t|=5，解得t=522或t=722，
故甲、乙两车相距不超过5km时，522≤t≤722，故④正确；
综上，结论正确的是①②④；
故答案为：①②④．
先求出甲乙的速度，再逐项分析即可．
本题考查了函数图象，主要利用了路程、速度、时间三者之间的关系，准确识图获取必要的信息是解题的关键．
17.【答案】解：(1)原式=3x(y+2)；
(2)原式=2(a2−1)
=2(a+1)(a−1)．
【解析】(1)利用提公因式法即可求解；
(2)综合利用提公因式法和公式法即可求解．
本题考查因式分解，掌握提取公因式法和公式法分解因式是解题关键．
18.【答案】证明：∵∠ACB=∠DEF=90°，
在Rt△ACB和Rt△DEF中，
AB=DFAC=DE，
∴Rt△ACB≌Rt△DE(HL)．
∴BC=FE．
∴BC−CE=FE−CE．
即BE=CF．
【解析】先证明Rt△ACB≌Rt△DEF，根据全等三角形的性质得出BC=FE，进而即可得证．
本题考查了全等三角形的性质与判定，熟练掌握HL证明全等三角形是解题的关键．
19.【答案】解：4(x−1)+3≤2x+5，
去括号，得
4x−4+3≤2x+5，
移项及合并同类项，得
2x≤6，
系数化为1，得
x≤3，
其解集在数轴上表示如下，
．
【解析】根据所求不等式的特点，可知要去括号、移项及合并同类项、系数化为1，即可求得不等式的解集，然后在数轴上表示即可．
本题考查解一元一次不等式、在数轴表示不等式的解集，解答本题的关键是明确解一元一次不等式的方法．
20.【答案】解：(1)如图所示：

(2)如图所示：
以下情形之一即可．
或 或
(3)如图所示：

【解析】(1)画出将阴影部分图形沿右平移3个单位长度后的图形即可；
(2)把一个图形绕着某个点旋转180°，如果旋转后的图形与原图形重合，则该图形是中心对称图形；
(3)将阴影部分的图形每个顶点均绕点O按顺时针方向旋转60°即可．
本题考查了平移、旋转作图，补图使原图形成为中心对称图形．关键是掌握图形变换的定义．
21.【答案】解：(1)如图所示，点D即为所求作的点；

(2)由(1)得，AD⊥BC，
在Rt△ADC中，AC=10，∠C=30°．
∴AD=12AC=5．
∴CD= AC2−AD2=5 3．
∵∠B=45°，AD⊥BC，
∴∠BAD=∠B=45°．
∴BD=AD=5．
∴BC=BD+CD=5+5 3．
【解析】(1)以A为圆心画弧分别交BC于M、N，再分别以M、N为圆心，大于12MN长为半径画弧交于点E，连接AE与BC交点即为D；
(2)根据等腰直角三角形和30°直角三角形的性质结合勾股定理计算即可．
本题考查了垂直作图，30°直角三角形的性质，勾股定理，解题的关键是熟记作垂线的作图步骤．
22.【答案】解：(1)设购买甲种礼盒x个，则购买乙种礼盒(80−x)个．根据题意，得
200x+350(80−x)≤19000．
解得x≥60．
∴甲种礼盒最少可以购买60个．
(2)解：设商家获得的利润为y元，根据题意，得
y=(200−a−120)x+(350−290)(80−x)
=(20−a)x+4800．
∵25≤a≤30，
∴20−a<0，
∴y随x的增大而减小，
∵x≥60，
∴当x=60时，y的最大值为6000−60a．
∵25≤a≤30，
∴当a=25时，y=6000−60×25=4500，利润最大为4500元．
【解析】(1)先设购买甲种礼盒x个，则购买乙种礼盒的个数，根据题意列出不等式，求出解集即可；
(2)设商家获得的利润为y元，根据题意列出一次函数，再讨论得出答案．
本题主要考查了一元一次不等式的应用，求一次函数的极值等，根据等量关系(不等关系)列出关系式(不等式)是解题的关键．
23.【答案】(1)解：∵AB=AC，
∴∠ABC=∠ACB=72°．
∴∠BAC=36°．
∵等腰三角形ABC与等腰三角形BED全等，
∴∠ABD=∠BAC=36°．
∴∠AMB=180°−∠ABD−∠BAC=108°；
(2)①证明：如图1，连接AE，由旋转可得AB=EB．

∴∠BEA=∠BAE．
∵△ABC≌△BED，
∴∠BAC=∠EBD．
∵EN//BD，
∴∠BEN=∠EBD．
∴∠BEN=∠BAC．
∴∠BEA−∠BEN=∠BAE−∠BAC．
即∠NEA=∠NAE．
∴AN=EN；
②解：EN=DM+CM或EN=DM−CM，理由如下：
如图3，当点M在AC延长线上时，连接BN，并延长交AE于点F．

∵BE=BA.NA=NE，
∵BF是AE的垂直平分线．
∵AB=EB，
∴∠ABF=∠EBF．
∵∠BNM=∠BAC+∠ABF，∠MBN=∠EBD+∠EBF，∠BAC=∠EBD，
∴∠MNB=∠MBN．
∴MN=MB．
∵AC=MN+AN−CM，BD=MB+DM，BD=AC，
∴DM=AN−CM．
由(1)得EN=AN，
∴EN=DM+CM．
当点M在AC上时，连接BN，并延长交AE于点F，如图4，

同理可得MN=MB．
∵AC=MN+AN+CM，BD=MB+DM，BD=AC，
∴DM=AN+CM，
由(1)得EN=AN，
∴EN=DM−CM．
综上，EN=DM+CM或EN=DM−CM．
【解析】(1)根据等腰三角形的性质、全等三角形的性质结合三角形的内角和求解即可；
(2)①证明∠BEA=∠BAE，∠BEN=∠BAC，可得∠NEA=∠NAE，进而可得结论；
②当点M在AC延长线上时，连接BN，并延长交AE于点F，证明∠MNB=∠MBN，可得MN=MB，然后利用线段的和差代换可得结论；当点M在AC上时，同理求解．
本题考查了全等三角形的性质、等腰三角形的判定和性质、线段垂直平分线的性质、三角形的内角和定理、平行线的性质等知识，熟练掌握相关图形的性质定理、进行线段和角之间的代换是解题的关键．