

2024年北京市清华附中高考数学统练试卷(二)(含解析)
展开1.抛物线y2=2x的焦点坐标是( )
A. (0,12)B. (0,−12)C. (−12,0)D. (12,0)
2.已知集合A={x|2x−3x>0},B={0,1,2,3,4},则A∩B=( )
A. {0}B. {1,2,3}C. {0,4}D. {3,4}
3.曲线y=f(x)与曲线y=csx关于x轴对称,则( )
A. f(x)=sinxB. f(x)=−sinxC. f(x)=csxD. f(x)=−csx
4.已知数列{an}为等差数列,{bn}为等比数列,a4=b4=4,则( )
A. b3b5≥a3a5B. b3+b5≥a3+a5C. b3b5≤a3a5D. b3+b5≤a3+a5
5.如图,在▱OACB中,E是AC的中点,F是BC上的一点,且BC=3BF,若OC=mOE+nOF,其中m,n∈R,则m+n的值为( )
A. 1B. 32C. 75D. 73
6.已知z−表示复数z的共轭复数,z1,z2为非零复数,“z1z2∈R”是“存在非零实数t,使得z1=tz2−”( )
A. 充分不必要条件B. 必要不充分条件
C. 充分必要条件D. 既不充分又不必要条件
7.斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致.如图是重庆千斯门嘉陵江大桥,共有10对永久拉索,在索塔两侧对称排列.已知拉索上端相邻两个锚的间距|PiPi+1|(i=1,2,3,⋯,9)均为3.4m,拉索下端相邻两个锚的间距|AiAi+1|(i=1,2,3,⋯,9)均为16m.最短拉索的锚P1,A1满足|OP1|=66m,|OA1|=86m,则最长拉索所在直线的斜率为( )
A. ±0.47B. ±0.45C. ±0.42D. ±0.40
8.已知三棱锥S−ABC中,SC=2 3,AB=2,E,F分别是SA,BC的中点,EF=1,则EF与AB所成的角大小为( )
A. π4
B. π3
C. 2π3
D. 3π4
9.已知函数f(x)=1−|x+1|,x<0x2−2x,x≥0,若实数m∈[−2,0],则|f(x)−f(−1)|在区间[m,m+2]上的最大值的取值范围是( )
A. [1,4]B. [2,4]C. [1,3]D. [1,2]
10.已知半圆C:x2+y2=1(y≥0),A、B分别为半圆C与x轴的左、右交点,直线m过点B且与x轴垂直,点P在直线m上,纵坐标为t,若在半圆C上存在点Q使∠BPQ=π3,则t的取值范围是( )
A. [−2 33,0)∪(0, 3]B. [− 3,0)∪(0,2 33]
C. [− 33,0)∪(0, 33]D. [−2 33,0)∪(0,2 33]
二、填空题:本题共5小题,每小题5分,共25分。
11.在(1−2x)5−(1−x)4的展开式中,含x3项的系数为______.
12.请写出一个焦点在y轴上,且与直线y=2x没有交点的双曲线的标准方程: .
13.已知函数f(x)=|x2+ax+b|在区间[0,4]上的最大值为M,当实数a,b变化时,M最小值为______.
14.已知函数f(x)=sin(ωx+φ),其中ω>0,且|f(x)|≤f(π6)恒成立,f(x)在(π3,5π6)上单调,则ω的取值范围是______.
15.数列{an}的前n项和为Sn,若数列{an}与函数f(x)满足:①f(x)的定义域为R;②数列{an}与函数f(x)均单调递增;③∃n∈N*使Sn=f(an)成立,则称数列{an}与函数f(x)具有“单调偶遇关系”.有下面四个结论:
①an=2n+1与f(x)=x具有“单调偶遇关系”
②an=2n与f(x)=2x−2不具有“单调偶遇关系”
③与数列{2n+1}具有“单调偶遇关系的函数有有限个
④与数列{2n}具有“单调偶遇关系”的函数有无数个
其中正确结论的序号为______.
三、解答题:本题共6小题,共85分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题13分)
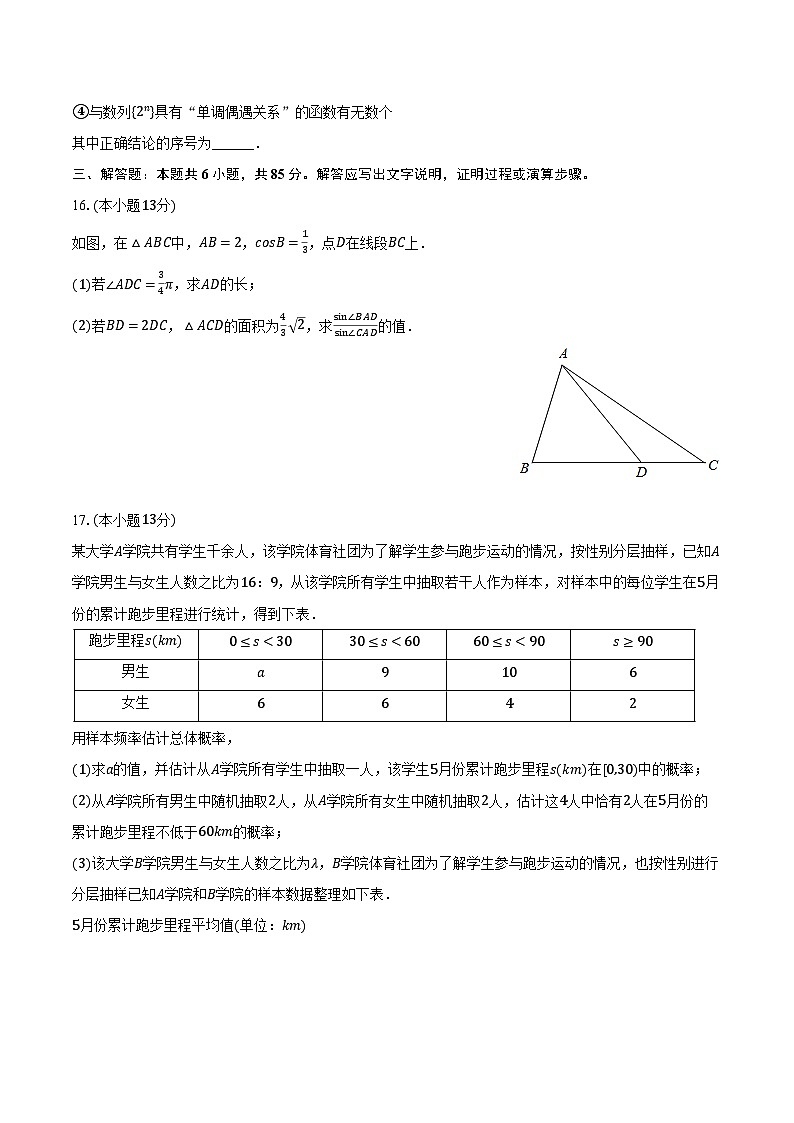
如图,在△ABC中,AB=2,csB=13,点D在线段BC上.
(1)若∠ADC=34π,求AD的长;
(2)若BD=2DC,△ACD的面积为43 2,求sin∠BADsin∠CAD的值.
17.(本小题13分)
某大学A学院共有学生千余人,该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,已知A学院男生与女生人数之比为16:9,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
用样本频率估计总体概率,
(1)求a的值,并估计从A学院所有学生中抽取一人,该学生5月份累计跑步里程s(km)在[0,30)中的概率;
(2)从A学院所有男生中随机抽取2人,从A学院所有女生中随机抽取2人,估计这4人中恰有2人在5月份的累计跑步里程不低于60km的概率;
(3)该大学B学院男生与女生人数之比为λ,B学院体育社团为了解学生参与跑步运动的情况,也按性别进行分层抽样已知A学院和B学院的样本数据整理如下表.
5月份累计跑步里程平均值(单位:km)
设A学院样本中学生5月份累计跑步里程平均值为x−A,B学院样本中学生5月份累计跑步里程平均值为x−B,是否存在λ,使得x−A≥x−B?如果存在,求λ的最大值;如果不存在,说明理由.
18.(本小题14分)
四棱锥P−ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,PA⊥AB,E为棱PA的中点,过点B,C,E的平面交棱PD于点F.
(1)求证:F为PD中点;
(2)若PA=AB=2,PD=3,再从条件①,条件②,条件③中选择一个作为已知,使四棱锥唯一确定,求二面角D−CF−E的余弦值.
条件①:PC⊥BD
条件②:PC=BC
条件③:PC与平面ABCD所成角的正切值为2
如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
19.(本小题15分)
已知点(1,32)在椭圆E:x2a2+y2b2=1(a>b>0)上,且E的离心率为12.
(1)求E的方程;
(2)设F为椭圆E的右焦点,点P(m,n)是E上的任意一点,直线PF与直线3mx+4ny=0相交于点Q,求|PQ|的值.
20.(本小题15分)
设函数f(x)=ln(ax+1)−x,a∈R,曲线y=f(x)在原点处的切线为x轴.
(1)求a的值;
(2)求方程f(x)=−x2x+2的解;
(3)证明:e<(20242023)2023.5.
21.(本小题15分)
设k是正整数,集合A至少有两个元素,且A⊆N*.如果对于A中的任意两个不同的元素x,y,都有|x−y|≠k,则称A具有性质P(k).
(1)试判断集合B={1,2,3,4}和C={1,4,7,10}是否具有性质P(2)?并说明理由;
(2)若集合A={a1,a2,⋯,a12}⊆{1,2,⋯,20},求证:A不可能具有性质P(3);
(3)若集合A⊆{1,2,⋯,2023},且同时具有性质P(4)和P(7),求集合A中元素个数的最大值.
答案和解析
1.【答案】D
【解析】【分析】
本题给出抛物线方程,求它的焦点坐标,着重考查了抛物线的标准方程和简单性质等知识,属于基础题.
根据抛物线方程,可得2p=2,得p2=12.再根据抛物线是开口向右以原点为顶点的抛物线,即可得到它的焦点坐标.
【解答】
解:∵抛物线方程为y2=2x,
∴2p=2,得p2=12,
∵抛物线开口向右且以原点为顶点,
∴抛物线的焦点坐标是(12,0),
故选D.
2.【答案】C
【解析】解:当x=0时,满足2x−3x>0,
当x=1时,不满足2x−3x>0,
当x=2时,不满足2x−3x>0,
当x=3时,不满足2x−3x>0,
当x=4时,满足2x−3x>0,
B={0,1,2,3,4},
则A∩B={0,4}.
故选:C.
根据已知条件,结合交集的定义,即可求解.
本题主要考查交集及其运算,属于基础题.
3.【答案】D
【解析】解:曲线y=f(x)与曲线y=csx关于x轴对称,
则f(x)=−csx.
故选:D.
根据已知条件,结合函数关于x轴的性质,即可求解.
本题主要考查余弦函数的图象,属于基础题.
4.【答案】A
【解析】解:由数列{an}为等差数列,{bn}为等比数列,a4=b4=4,
可得a3+a5=2a4=8,b3b5=b42=16,
由a3a5≤(a3+a52)2=16,可得a3a5≤b3b5,故A正确,C错误;
当b1>0,可得b3+b5≥2 b3b5=8=a3+a5;
当b1<0,可得b3+b5≤−2 b3b5=−8
由等差数列和等比数列的中项性质和基本不等式、不等式的性质,可得结论.
本题考查等差数列和等比数列的中项性质,以及基本不等式的运用,考查转化思想和运算能力,属于基础题.
5.【答案】C
【解析】【分析】
本题考查了平面向量的线性运算问题,解题时应熟知平面向量的三角形合成法则,是基础题目.
由平面向量的线性运算得:OA=65OE−35OF,OB=65OF−25OE,OC=OA+OB,由此求得m,n的值即可.
【解答】
解:因为OF=OB+BF=OB+13OA,OE=OA+AE=OA+12OB,
所以OA=65OE−35OF,OB=65OF−25OE,
又OC=OA+OB=65OE−35OF+65OF−25OE=45OE+35OF,
所以m=45,n=35,
故m+n=75,
故选:C.
6.【答案】C
【解析】解:根据题意,z1,z2为非零复数,设z1=a+bi,z2=c+di,(a、b、c、d∈R且实数a、b不同时为0,实数c、d不同时为0),
由于z1z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i,
若z1z2∈R,则ad+bc=0,
又由a、b不同时为0,c、d不同时为0,必存在非零实数t,使得a=ctb=−dt,
则有z1=tz2−,
反之,若z1=tz2−,即a=ctb=−dt,变形可得ad+bc=0,
又由z1z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i=0;
故“z1z2∈R”是“存在非零实数t,使得z1=tz2−”的充分必要条件.
故选:C.
根据题意,设z1=a+bi,z2=c+di,实数a、b不同时为0,实数c、d不同时为0,由复数的乘法公式和共轭复数的定义分析“z1z2∈R”和“存在非零实数t,使得z1=tz2−”的关系,即可得答案.
本题考查复数的计算,涉及充分必要条件的判断,属于基础题.
7.【答案】C
【解析】解:根据题意,最短拉索的锚P1,A1满足|OP1|=66m,|OA1|=86m,且|PiPi+1|(i=1,2,3,⋯,9)均为3.4m,拉索下端相邻两个锚的间距|AiAi+1|(i=1,2,3,⋯,9)均为16m,
则|OA10|=|OA1|+|A1A10|=86+9×16=230,
又|OP10|=|OP1|+|P1P10|=66+9×3.4=96.6,
则最长拉索所在直线的斜率kA10P10=−tan∠OA10P10=−96.6230=−0.42,
同理,最长拉索所在直线的斜率kB10P10=0.42,
故选:C.
根据题意,利用已知长度可分别计算|OA10|,|OP10|,再利用斜率定义可解.
本题考查斜率的计算公式,属于基础题.
8.【答案】B
【解析】【分析】
本题考查了异面直线所成角的求法,利用余弦定理解三角形,属于一般题.
取AC中点D,连接DE、DF,由E,F分别是SA,BC的中点,得DESC,DFAB,进而得EF与AB所成的角的平面角为∠EFD(或其补角),然后利用余弦定理求解即可.
【解答】
解:取AC中点D,连接DE、DF,
因为E,F分别是SA,BC的中点,
所以DESC,DFAB,
所以EF与AB所成的角的平面角为∠EFD(或其补角),
由SC=2 3,AB=2,得DE= 3,DF=1,
又EF=1,
则cs∠EFD=DF2+EF2−DE22×DF×EF=1+1−32×1×1=−12,
所以∠EFD=2π3,
所以EF与AB所成的角大小为π3,
故选B.
9.【答案】D
【解析】【分析】
本题主要考查分段函数的图象及解决含参数最值问题的能力,属于一道有难度的题.
令g(x)=f(x)−f(−1),根据题设条件求出g(x)的表达式,画出其图象,再对m进行讨论,求出|g(x)|的最大值的表达式,进而解决其范围问题.
【解答】
解:∵函数f(x)=1−|x+1|,x<0x2−2x,x≥0,∴f(x)−f(−1)=x+1,x≤−1−x−1,−1
①当m=−2时,g(x)=x+1,x∈[−2,−1]−x−1,x∈(−1,0],此时|g(x)|max=1;
②m∈(−2,−1)时,
|g(x)|max=−g(m+2)=−[(m+2)2−2(m+2)−1]=−m2−2m+1∈(1,2);
③当m=−1时,g(x)=−x−1,x∈[−1,0]x2−2x−1,x∈(0,1],此时|g(x)|max=2,
④当m∈(−1,0)时,|g(x)|max=−g(m+2)=−[(m+2)2−2(m+2)−1]
=−m2−2m+1∈(1,2);
⑤当m=0时,g(x)=x2−2x−1,x∈[0,2],此时|g(x)|max=2.
综上,最大值的取值范围为[1,2].
故选:D.
10.【答案】A
【解析】解:根据题意,设PQ与x轴交于点T,则|PB|=|t|,
由于BP与x轴垂直,且∠BPQ=π3,则在Rt△PBT中,
|BT|= 33|PB|= 33|t|,
当P在x轴上方时,PT与半圆有公共点Q,PT与半圆相切时,|BT|有最大值3,此时t有最大值 3,
当P在x轴下方时,当Q与A重合时,|BT|有最大值2,|t|有最大值−2 33,则t取得最小值−2 33,
t=0时,P与B重合,不符合题意,
则t的取值范围为[−2 33,0)∪(0, 3];
故选:A.
根据题意,设PQ与x轴交于点T,分析可得在Rt△PBT中,|BT|= 33|PB|= 33|t|,分p在x轴上方、下方和x轴上三种情况讨论,分析|BT|的最值,即可得t的范围,综合可得答案.
本题考查直线与圆方程的应用,涉及直线与圆的位置关系,属于基础题.
11.【答案】−76
【解析】解:在(1−2x)5−(1−x)4的展开式中,
则含x3项的系数为C53(−2)3−[C43(−1)3]=−76.
故答案为:−76.
根据已知条件,结合二项式定理,即可求解.
本题主要考查二项式定理,属于基础题.
12.【答案】y24−x2=1(答案不唯一,满足a≥2b>0的焦点在y轴上的标准方程均可)
【解析】解:设焦点在y轴上的双曲线的标准方程为y2a2−x2b2=1,(a>0,b>0),
∴该双曲线的渐近线方程为y=±abx,
又该双曲线与直线y=2x没有交点,
∴ab≥2,
∴a≥2b,
取a=2,b=1,
则可得满足题意的一个双曲线方程为y24−x2=1,
故答案为:y24−x2=1(答案不唯一,满足a≥2b>0的焦点在y轴上的标准方程均可).
设焦点在y轴上的双曲线的标准方程为y2a2−x2b2=1,(a>0,b>0),根据题意可得ab≥2,再取一组值,即可得解.
本题考查双曲线的几何性质,不等式思想,属基础题.
13.【答案】2
【解析】解:f(x)=|x2−4x+(a+4)x+b|=|x2−4x−[−(a+4)x−b]|,函数可理解为:
当横坐标相同时,函数g(x)=x2−4x,x∈[0,4]与函数h(x)=−(a+4)x−b,x∈[0,4]图象上点的纵向距离,
则M即为函数g(x)=x2−4x与函数h(x)=−(a+4)x−b图象上点的纵坐标差的绝对值的最大值,
由图象可知:当函数h(x)的图象刚好为y=−2时,M取得最小值为2,此时−(a+4)=0,且−b=−2,即a=−4,b=2.
故答案为:2.
根据题意,可得f(x)=|x2−4x−[−(a+4)x−b]|,则M即为函数g(x)=x2−4x与函数h(x)=−(a+4)x−b图象上点的纵坐标差的绝对值的最大值,因此作出图象,根据图象观察即可得出答案.
本题主要考查二次函数的图象与性质、函数的最值及其几何意义等知识,属于中档题.
14.【答案】(0,32]
【解析】解:因为f(x)=sin(ωx+φ),其中ω>0,且|f(x)|≤f(π6)恒成立,
所以f(π6)=1,即π6ω+φ=2kπ+π2(k∈Z),
解得φ=π2−ωπ6+2kπ,k∈Z.
由π3
即π2+ωπ6+2kπ<ωx+φ<π2+2ωπ3+2kπ,k∈Z,
若函数f(x)在(π3,5π6)上单调递增,
则−π2+2kπ≤π2+ωπ6+2kπ<π2+2ωπ3+2kπ≤π2+2kπ,k∈Z,
即−π2+2kπ≤π2+ωπ6+2kππ2+ωπ6+2kπ<π2+2ωπ3+2kππ2+2ωπ3+2kπ≤π2+2kπ,k∈Z,解得ω≥−6ω>0ω≤0,则不等式组无解;
若函数f(x)在(π3,5π6)上单调递减,
则π2+2kπ≤π2+ωπ6+2kπ<π2+2ωπ3+2kπ≤3π2+2kπ,k∈Z,
即π2+2kπ≤π2+ωπ6+2kππ2+ωπ6+2kπ<π2+2ωπ3+2kππ2+2ωπ3+2kπ≤3π2+2kπ,k∈Z,解得ω≥0ω>0ω≤32,则0<ω≤32,
所以实数ω的取值范围为(0,32].
故答案为:(0,32].
由|f(x)|≤f(π6)可知f(π6)=1,则φ=π2−ωπ6+2kπ,k∈Z,由正弦函数的单调性建立不等式组,解之即可求解.
本题考查正弦函数的单调性,考查运算求解能力,属于中档题.
15.【答案】①④.
【解析】解:对于①:数列{an}中,由an=2n+1可知任意两项不相等,f(x)=x定义域为R满足①,
数列an=2n+1和f(x)=x均单调递增满足②,
{an}的前n项和Sn=n(3+2n+1)2=n2+2n,
由Sn=f(an)得n2+2n=2n+1,解得n=1,
所以∃n∈N*使Sn=f(an)成立,满足③,故①正确;
对于②:数列{an}中,由an=2n可知任意两项不相等,f(x)=2x−2定义域为R满足①,
数列an=2n和f(x)=2x−2均单调递增满足②,
an的前n项和Sn=2n+1−2,由Sn=f(an)得2n+1−2=2×2n−2恒成立,
所以∃n∈N*使Sn=f(an)成立满足③,
故an=2n与f(x)=2x−2具有“单调偶遇关系”,故②说法不正确;
对于③:以一次函数为例,f(x)=kx+b,Sn=n2+2n,Sn=f(an),即n2+2n=k(2n+1)+b,
整理得n2+(2−2k)n−(k+b)=0,只要方程有正整数解且k>0即可,如方程中取n=1,则有3=3k+b,
即k=1−b3,对b进行不同的取值即可保证数列{2n+1}具有“单调偶遇关系”的函数有无数组,故③说法不正确;
对于④:中Sn=2n+1−2令f(an)=λan.
由Sn=f(an)得2n+1−2=λ×2n,取λ=2−22n,即可保证Sn=f(an)恒成立,故选项④正确.
故答案为:①④.
根据“单调偶遇关系”的新定义可判断选项①,②;以一次函数为例,f(x)=kx+b可判断③;令f(an)=λan,通过计算可判断④,进而可得正确选项.
本题主要考查数列与函数的综合,考查运算求解能力,属于难题.
16.【答案】解:(1)∵△ABC中,csB=13,∴sinB=2 23.
∵∠ADC=34π,∴∠ADB=π4.
在△ABD中,由正弦定理可得ADsinB=ABsin∠ADB,
即AD2 23=2 22,∴AD=83;
(2)设DC=a,则BD=2a,
∵BD=2DC,△ACD的面积为43 2,
∴△ABC的面积为4 2=12×2×3a×2 23,
∴a=2,
∴AC= 4+36−2×2×6×13=4 2,
在△ABD中,由正弦定理可得4sin∠BAD=2sin∠ADB,
∴sin∠BAD=2sin∠ADB.
在△ACD中,由正弦定理可得2sin∠CAD=4 2sin∠ADC,
∴sin∠CAD= 24sin∠ADC,
∵sin∠ADB=sin∠ADC,
∴sin∠BADsin∠CAD=4 2.
【解析】本题考查正弦、余弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.
(1)△ABD中,由正弦定理可得AD的长;
(2)利用BD=2DC,△ACD的面积为43 2,求出a=2,利用余弦定理求出AC,利用正弦定理可得结论.
17.【答案】解:(1)依题意a+9+10+66+6+4+2=169,解得a=7,
所以在0,30)中的概率为7+67+9+10+6+6+6+4+2=1350.
(2)A学院所抽取的学生中男生有7+9+10+6=32人,
其中5月份的累计跑步里程不低于60km有10+6=16人,
女生有6+6+4+2=18人,
其中5月份的累计跑步里程不低于60km有4+2=6人,
所以在A学院所有男生中任取1人,跑步里程不低于60km的概率为1632=12,
在A学院所有女生中任取1人,跑步里程不低于60km的概率为618=13,
所以4人中恰有2人累计跑步里程不低于60km的概率为:
C22(12)2C20(1−13)2+C2112(1−12)C2113(1−13)+C20(12)2C22(13)2=1336;
(3)设B学院女生有x人,则男生有λx人,
xA−=1625×50+925×40=2325,
xB−=59λx+45xλx+45x=59λ+45λ+45,
依题意xA−≥xB−,即2325≥59λ+45λ+1,
显然λ>0,解得0<λ≤19,所以λ的最大值为19.
【解析】(1)先根据男女比即可求出a,再根据古典概型即可求出所求概率;
(2)先分别求出在A学院所有男生中任取1人,跑步里程不低于60km的概率及在A学院所有女生中任取1人,跑步里程不低于60km的概率,再根据乘法公式求解即可.
(3)设B学院女生人数为x,则男生人数为λx,求出x−A=x−B,即可得到不等式,解得即可.
本题考查古典概率模型公式,属于中档题.
18.【答案】(1)证明:因为底面ABCD为平行四边形,
所以AD//BC,
又AD⊂平面PAD,BC⊄平面PAD,
所以BC//平面PAD,
因为BC⊂平面BCFE,且平面BCFE∩平面PAD=EF,
所以BC//EF,
又E为棱PA的中点,所以F为PD中点.
(2)解:选择①:因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PA⊥AB,PA⊂平面PAB,
所以PA⊥平面ABCD,
所以PC在底面ABCD内的投影为AC,
因为PC⊥BD,所以AC⊥BD,
又底面ABCD为平行四边形,所以四边形ABCD是菱形,所以AD=AB=2,
因为PA⊥平面ABCD,且AD⊂平面ABCD,
所以PA⊥AD,
所以PD= PA2+AD2= 22+22=2 2≠3,
故四棱锥P−ABCD不存在.
选择②:因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PA⊥AB,PA⊂平面PAB,
所以PA⊥平面ABCD,
因为AD、AC⊂平面ABCD,所以PA⊥AD,PA⊥AC,
所以AD= PD2−PA2= 32−22= 5=BC=PC,
所以AC= PC2−PA2= 5−22=1,
所以AC2+AB2=BC2,即AB⊥AC,
故以A为坐标原点,建立如图所示的空间直角坐标系,
则C(0,1,0),D(−2,1,0),E(0,0,1),P(0,0,2),F(−1,12,1),
所以CF=(−1,−12,1),CD=(−2,0,0),EF=(−1,12,0),
设平面CDF的法向量为m=(x,y,z),则m⋅CF=0m⋅CD=0,即−x−12y+z=0−2x=0,
取z=1,则x=0,y=2,所以m=(0,2,1),
设平面CEF的法向量为n=(a,b,c),则n⋅CF=0n⋅EF=0,即−a−12b+c=0−a+12b=0,
取a=1,则b=2,c=3,所以n=(1,2,3),
所以cs
由图可知,二面角D−CF−E为钝角,
所以二面角D−CF−E的余弦值为− 7010.
选择③:因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PA⊥AB,PA⊂平面PAB,
所以PA⊥平面ABCD,
所以∠ACP即为PC与平面ABCD所成角,即tan∠ACP=2,
在Rt△PAC中,tan∠ACP=2=PAAC=2AC,所以AC=1,
因为PA⊥平面ABCD,AD⊂平面ABCD,所以PA⊥AD,
所以AD= PD2−PA2= 32−22= 5=BC,
所以AC2+AB2=BC2,即AB⊥AC,
故以A为坐标原点,建立如图所示的空间直角坐标系,
则C(0,1,0),D(−2,1,0),E(0,0,1),P(0,0,2),F(−1,12,1),
所以CF=(−1,−12,1),CD=(−2,0,0),EF=(−1,12,0),
设平面CDF的法向量为m=(x,y,z),则m⋅CF=0m⋅CD=0,即−x−12y+z=0−2x=0,
取z=1,则x=0,y=2,所以m=(0,2,1),
设平面CEF的法向量为n=(a,b,c),则n⋅CF=0n⋅EF=0,即−a−12b+c=0−a+12b=0,
取a=1,则b=2,c=3,所以n=(1,2,3),
所以cs
由图可知,二面角D−CF−E为钝角,
所以二面角D−CF−E的余弦值为− 7010.
【解析】(1)由AD//BC,可得BC//平面PAD,再利用线面平行的性质定理知BC//EF,从而得证;
(2)选择①:由面面垂直的性质定理可证PA⊥平面ABCD,结合三垂线定理推出四边形ABCD是菱形,从而得PD=2 2≠3,进而知四棱锥P−ABCD不存在;
选择②:由面面垂直的性质定理可证PA⊥平面ABCD,再利用勾股定理证明AB⊥AC,于是以A为坐标原点建立空间直角坐标系,利用向量法求二面角,即可得解;
选择③:由面面垂直的性质定理可证PA⊥平面ABCD,根据线面角的定义知tan∠ACP=2,再利用勾股定理证明AB⊥AC,于是以A为坐标原点建立空间直角坐标系,利用向量法求二面角,即可得解.
本题考查立体几何的综合应用,熟练掌握线面平行的判定定理与性质定理,面面垂直的性质定理,利用向量法求二面角是解题的关键,考查空间立体感,逻辑推理能力和运算能力,属于中档题.
19.【答案】解:(1)由题意得1a2+94b2=1,ca=12,a2=b2+c2,解得a=2,b= 3,c=1.
所以椭圆E的方程为x24+y23=1.
(2)因为点P(m,n)是E上的任意一点,所以3m2+4n2=12.
①当m=1时,点P(1,32)或P(1,−32).
当点P(1,32)时,直线PF与直线x+2y=0相交于点Q(1,−12),此时|PQ|=2.
当点P(1,−32)时,直线PF与直线x−2y=0相交于点Q(1,12),此时|PQ|=2.
②当m≠1时,直线PF的方程为y=nm−1(x−1),
由y=nm−1(x−1)3mx+4ny=0,可得x=4n212−3my=−mn4−m,所以Q(4n212−3m,−mn4−m).
所以|PQ|2=(m−4n212−3m)2+(n−−mn4−m)2=(12m−3m2−4n212−3m)2+(4n−mn+mn4−m)2
=(4m−44−m)2+(4n4−m)2=(4m−4)2+16n2(4−m)2=(4m−4)2+4(12−3m2)(4−m)2
=4(m2−8m+16)(4−m)2=4(m−4)2(4−m)2=4,
所以|PQ|=2.
综上所述,|PQ|=2.
【解析】本题主要考查椭圆的性质及标准方程,直线与椭圆的综合,考查方程思想与运算求解能力,属于中档题.
(1)由题意得1a2+94b2=1,ca=12,a2=b2+c2,求出a,b即可得椭圆方程;
(2)由题意可得3m2+4n2=12,当m=1时,求出|PQ|的值;当m≠1时,联立直线PF与直线3mx+4ny=0的方程求出点Q的坐标,根据3m2+4n2=12求解|PQ|2即可.
20.【答案】解:(1)因为f(x)=ln(x+1)−ax(x>−1),
所以f′(x)=1x+1−a,
因为曲线y=f(x)在原点处的切线为x轴,
所以f′(0)=1−a=0,即a=1;
(2)由题,方程f(x)=−x2x+2可化为ln(x+1)−2xx+2=0,
令g(x)=ln(x+1)−2xx+2(x>−1),
则g′(x)=1x+1−4(x+2)2=(x+2)2−4(x+1)(x+1)(x+2)2=x2(x+1)(x+2)2≥0,
所以g(x)在(−1,+∞)上单调递增,
又g(0)=0,所以g(x)在(−1,+∞)上有唯一零点x=0,
即方程f(x)=−x2x+2有唯一解x=0;
证明:(3)要证e<(20242023)2023.5,
即证1<2023.5×ln20242023,
即证ln20242023>12023.5,
由(2)易得ln(x+1)>2xx+2,x∈(0,+∞),
所以ln20242023=ln(12023+1)>2×1202312023+2=24047=12023.5得证.
【解析】(1)根据题意可知f(x)在x=0处的导数值为0,解方程即可;
(2)构造函数g(x)=ln(x+1)−2xx+2,利用导数证明其单调性,再通过观察法得x=0是g(x)的零点,从而得解;
(3)要证e<(20242023)2023.5,即证ln20242023>12023.5,然后利用(2)中结论即可证明.
本题考查了导数的综合应用,属于中档题.
21.【答案】解:(1)因为B={1,2,3,4},
又1∈N*,2∈N*,3∈N*,4∈N*,但|4−2|=2,
所以集合B不具有性质P(2),
因为C={1,4,7,10},
又1∈N*,4∈N*,7∈N*,10∈N*,
但|4−1|=3,|7−1|=6,|10−1|=9,|7−4|=3,|10−4|=6,|10−7|=3,
所以集合C具有性质P(2),
(2)证明:将集合{1,2,⋯,20}中的元素分为如下11个集合,
{1,4},{2,5},{3,6},{7,10},{8,11}.{9,12},{13,16},{14,17},{15,18},{19},{20},
所以从集合{1,2,⋯,20}中取12个元素,则前9个集合至少要选10个元素,
所以必有2个元素取自前9个集合中的同一集合,即存在两个元素其差为3,
所以A不可能具有性质P(3);
(3)先说明连续11项中集合A中最多选取5项,
以1,2,3⋅⋅⋅,11为例.
构造抽屉{1,8},{2,9},{3,10},{4,11},{5},{6},{7}.
①5,6,7同时选,因为具有性质P(4)和P(7),
所以选5则不选1,9;选6则不选2,10;选7则不选3,11;
则只剩4,8.故1,2,3⋅⋅⋅,11中属于集合A的元素个数不超过5个.
②5,6,7选2个,
若只选5,6,则1,2,9,10,7不可选,又{4,11}只能选一个元素,
3,8可以选,故1,2,3⋅⋅⋅,11中属于集合A的元素个数不超过5个.
若选5,7,则只能从2,4,8,10中选,但4,8不能同时选,
故1,2,3⋅⋅⋅,11中属于集合A的元素个数不超过5个.
若选6,7,则2,3,10,11,5不可选,又{1,8}只能选一个元素,
4,9可以选,故1,2,3⋅⋅⋅,11中属于集合A的元素个数不超过5个.
③5,6,7中只选1个,
又四个集合{1,8},{2,9},{3,10},{4,11}每个集合至多选1个元素,
故1,2,3⋅⋅⋅,11中属于集合A的元素个数不超过5个.
由上述①②③可知,连续11项自然数中属于集合A的元素至多只有5个,
如取1,4,6,7,9.
因为2023=183×11+10,则把每11个连续自然数分组,前183组每组至多选取5项;
从2014开始,最后10个数至多选取5项,故集合A的元素最多有184×5=920个.
给出如下选取方法:从1,2,3⋅⋅⋅,11中选取1,4,6,7,9;
然后在这5个数的基础上每次累加11,构造183次.
此时集合A的元素为:1,4,6,7,9;12,15,17,18,20;23,26,28,29,31;⋅⋅⋅⋅⋅⋅;
2014,2017,2019,2020,2022,共920个元素.
经检验可得该集合符合要求,故集合A的元素最多有920个.
【解析】(1)根据定义判断B,C是否具有性质P(2)即可;
(2)将{1,2,⋯,20}分为11个子集,结合抽屉原理证明结论;
(3)先证明连续11个自然数中至多有5个元素属于A,由此可得集合A中元素个数不超过920个,再举例说明存在含有920个元素的满足要求的集合A.
本题考查集合新定义,考查学生计算能力,属于难题.跑步里程s(km)
0≤s<30
30≤s<60
60≤s<90
s≥90
男生
a
9
10
6
女生
6
6
4
2
学院性别
A
B
男生
50
59
女生
40
45
2022-2023学年北京市清华大学附中高一(下)期末数学试卷(含详细答案解析): 这是一份2022-2023学年北京市清华大学附中高一(下)期末数学试卷(含详细答案解析),共21页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年北京市清华附中高一(上)期末数学试卷(含解析): 这是一份2022-2023学年北京市清华附中高一(上)期末数学试卷(含解析),共11页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
北京市海淀区清华附中2022~2023学年第二学期高三数学统练(2): 这是一份北京市海淀区清华附中2022~2023学年第二学期高三数学统练(2),共15页。












