中考数学复习章节限时练6圆含答案

这是一份中考数学复习章节限时练6圆含答案，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(本大题共7小题，每小题5分，共35分)
1．如图，在半径为5 cm的⊙O中，弦AB＝6 cm, OC⊥AB于点C，则OC的长为（B）
A．3 cm B．4 cm C．5 cm D．6 cm
2.如图，AB是⊙O的直径，∠BAC＝50°，则∠D的度数为（B）
A．20° B．40° C．50° D．80°
3．在矩形ABCD中，AB＝3，AD＝4.若以点A为圆心，4为半径作⊙A，则下列各点中在⊙A外的是（C）
A．点A B．点B
C．点C D．点D
4．如图，四边形ABCD内接于⊙O，CB＝CD，若∠BCD＝2∠BAD，则∠OBC的度数是（D）
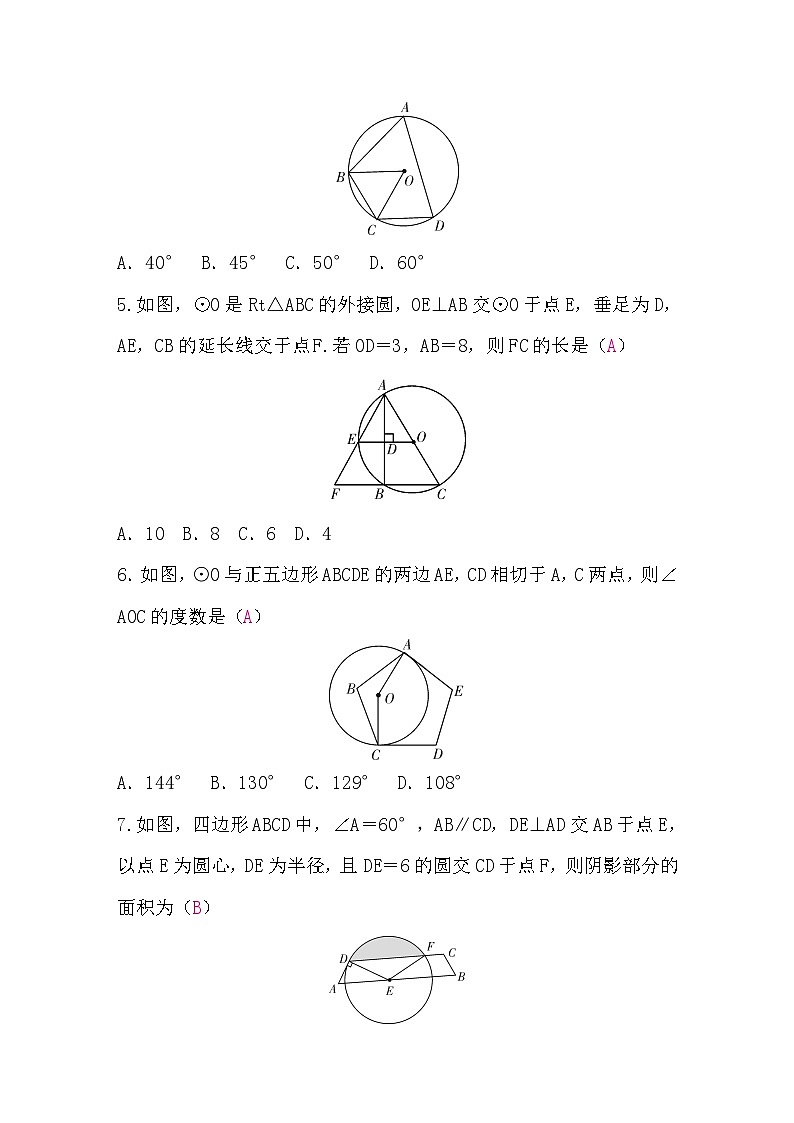
A．40° B．45° C．50° D．60°
5.如图，⊙O是Rt△ABC的外接圆，OE⊥AB交⊙O于点E，垂足为D，AE，CB的延长线交于点F.若OD＝3，AB＝8，则FC的长是（A）
A．10 B．8 C．6 D．4
6．如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，C两点，则∠AOC的度数是（A）
A．144° B．130° C．129° D．108°
7.如图，四边形ABCD中，∠A＝60°，AB∥CD，DE⊥AD交AB于点E，以点E为圆心，DE为半径，且DE＝6的圆交CD于点F，则阴影部分的面积为（B）
A．6π－9eq \r(3) B．12π－9eq \r(3)
C．6π－eq \f(9\r(3),2) D．12π－eq \f(9\r(3),2)
二、填空题(本大题共4小题，每小题5分，共20分)
8．如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为3，则BD的长为3eq \r(3).

9.如图，已知⊙O的周长为8π，则该圆内接正六边形ABCDEF的边心距OG为2eq \r(3).
10．如图，⊙O是△ABC的内切圆，D，E分别为边AB, AC上的点，且DE为⊙O的切线，若△ABC的周长为25, BC的长是9，则△ADE的周长是7.
11．如图，从一个腰长为60 cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，则此扇形的弧长为20πcm.
三、解答题(本大题共2小题，共45分)
12．(20分)如图，△ABC内接于⊙O，AB是⊙O的直径．直线l与⊙O相切于点A，在l上取一点D使得DA＝DC，线段DC，AB的延长线交于点E.
(1)求证：直线DC是⊙O的切线；
(2)若BC＝2，∠CAB＝30°，求图中阴影部分的面积(结果保留π)．
(1)证明：连接OC,
∵AB是⊙O的直径，
直线l与⊙O相切于点A，
∴∠DAB＝90°，
∵DA＝DC，OA＝OC，
∴∠DAC＝∠DCA，∠OAC＝∠OCA，
∴∠DCO＝∠DAO＝90°，∴OC⊥CD，
∵OC为⊙O的半径，∴直线DC是⊙O的切线．
(2)解：∵∠CAB＝30°，∴∠BOC＝2∠CAB＝60°，
∵OC＝OB，∴△COB是等边三角形，
∴OC＝OB＝BC＝2，∴CE＝eq \r(3)OC＝2eq \r(3)，
∴阴影部分的面积为
S△OCE－S扇形COB＝eq \f(1,2)×2×2eq \r(3)－eq \f(60·π×22,360)
＝2eq \r(3)－eq \f(2π,3).
13．(25分)如图，AB为⊙O的直径，点C，D为⊙O上异于A，B的两点，连接CD，过点C作CE⊥DB，交DB的延长线于点E，连接AC，AD，BC，若∠ABD＝2∠BDC.
(1)求证：CE是⊙O的切线；
(2)求证：△ABC∽△CBE；
(3)若⊙O的半径为5，tan∠BDC＝eq \f(1,2)，求BE的长．
(1)证明：连接OC，
∴∠BOC＝2∠BDC，∵∠ABD＝2∠BDC，
∴∠BOC＝∠ABD，
∴OC∥DB，
∵CE⊥BD，∴CE⊥OC，
∵点C在⊙O上，∴CE是⊙O的切线．
(2)证明：∵OB＝OC，∴∠ABC＝∠OCB，
由(1)知OC∥BD，∴∠CBE＝∠OCB，
∴∠ABC＝∠CBE，∵AB是⊙O的直径，
∴∠ACB＝90°，∵CE⊥BD，
∴∠CEB＝90°＝∠ACB，∴△ABC∽△CBE.
(3)解：由(1)知∠BDC＝∠BAC，
∵tan∠BDC＝eq \f(1,2)，∴tan∠BAC＝eq \f(1,2)，
在Rt△ABC中，AB＝10，tan∠BAC＝eq \f(BC,AC)＝eq \f(1,2)，
∴AC＝2BC，根据勾股定理得BC2＋AC2＝AB2，
∴BC2＋4BC2＝102，
∴BC＝2eq \r(5)，由(2)知△ABC∽△CBE，
∴eq \f(BE,BC)＝eq \f(BC,AB)，∴eq \f(BE,2\r(5))＝eq \f(2\r(5),10)，
∴BE＝2，即BE的长为2.