2022年黑龙江省齐齐哈尔市部分学校中考数学模拟试卷

这是一份2022年黑龙江省齐齐哈尔市部分学校中考数学模拟试卷，共21页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1．（3分）2022的相反数的倒数是（ ）
A．﹣2022B．﹣|﹣2022|C．D．
2．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
3．（3分）下列计算正确的是（ ）
A．2a2+2a3＝2a5B．2a﹣1＝
C．（﹣）0＝0D．﹣a3÷a＝﹣a2
4．（3分）甲乙两名同学进行了10次投掷铅球的测试，经计算，他们的平均成绩相同，通常还需要比较他们成绩的（ ）
A．众数B．中位数C．方差D．平均数
5．（3分）如图，AB∥CD，AD＝CD，则∠2的度数是（ ）
A．70°B．65°C．60°D．55°
6．（3分）如图摆放的正三棱柱的左视图是（ ）
A．B．C．D．
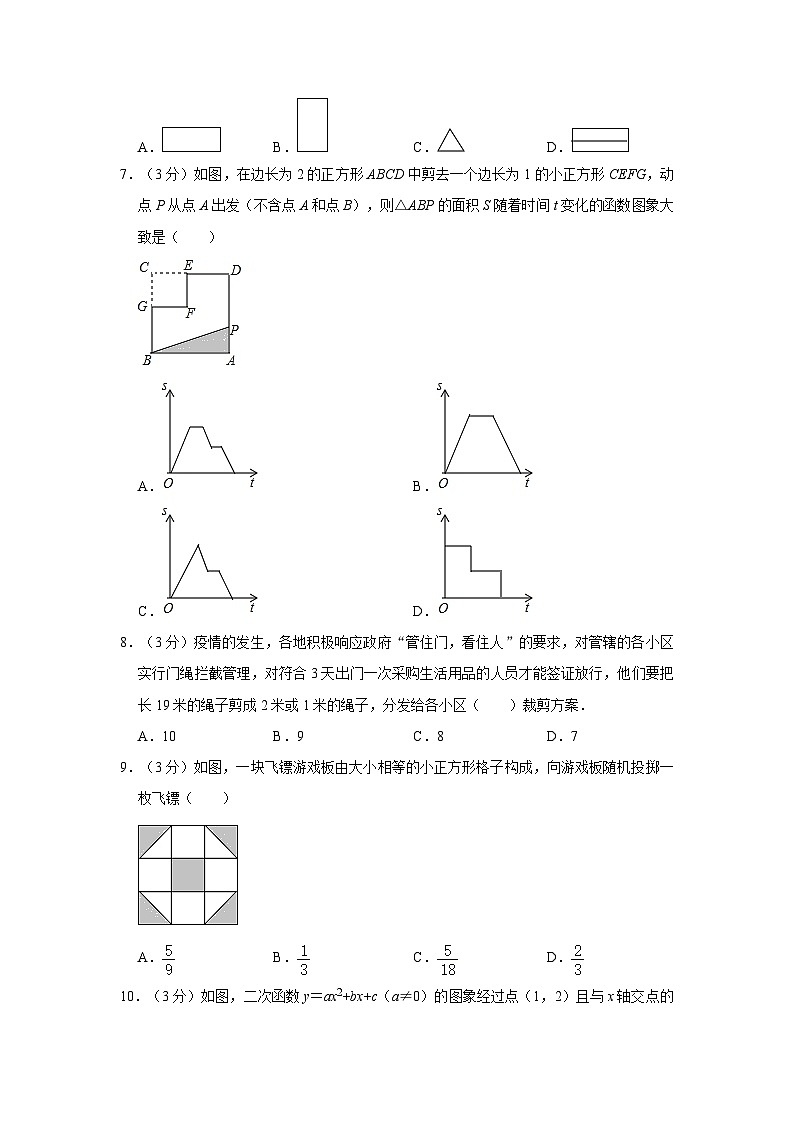
7．（3分）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（ ）
A．B．
C．D．
8．（3分）疫情的发生，各地积极响应政府“管住门，看住人”的要求，对管辖的各小区实行门绳拦截管理，对符合3天出门一次采购生活用品的人员才能签证放行，他们要把长19米的绳子剪成2米或1米的绳子，分发给各小区（ ）裁剪方案．
A．10B．9C．8D．7
9．（3分）如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖（ ）
A．B．C．D．
10．（3分）如图，二次函数y＝ax2+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0，1＜x2＜2，下列结论：①4a+2b+c＜0，②2a+b＜02+8a＞4ac，④a＜﹣1，⑤（a+c）2＜b2，其中结论正确的有（ ）
A．5个B．4个C．3个D．2个
二、填空题（本大题共7小题，每小题3分，共21分）
11．（3分）据2020年2月28日龙广新闻《新闻联播》消息，目前正是疫情预防关键时期，黑龙江省建设集团再次捐款280万元支持我省疫情防治工作．将280万这一数据用科学记数法表示为 ．
12．（3分）有下列四个条件：①AB＝BC，②∠ABC＝90°，③AC＝BD，使平行四边形ABCD为正方形（如图）．现在文文选择了②③ （填“对”或“不对”）．
13．（3分）扇形的面积是12π，它的弧长为6π，则这个扇形的圆心角的度数是 ．
14．（3分）关于x的分式方程的解为正数，则k的取值范围是 ．
15．（3分）如图，直线y＝﹣x与双曲线的图象交于A、B两点，连接BC，若S△ACB＝4，则k的值为 ．
16．（3分）等边△ABC，AB＝8，点D在直线AB上，则AD的长为 ．
17．（3分）如图，正方形AOBO2的顶点A的坐标为A（0，2），O1为正方形AOBO2的中心；以正方形AOBO2的对角线AB为边，在AB的右侧作正方形ABO3A1，O2为正方形ABO3A1的中心；再以正方形ABO3A1的对角线A1B为边，在A1B的右侧作正方形A1BB1O4，O3为正方形A1BB1O4的中心；再以正方形A1BB1O4的对角线A1B1为边，在A1B1的右侧作正方形A1B1O5A2，O4为正方形A1B1O5A2的中心：…；按照此规律继续下去，则点O2020的坐标为 ．
三.解答题（本大题共6个小题，共69分。解答应写出必要的文字说明，证明过程或演算步骤）
18．（10分）（1）计算：（﹣2020）0+|1﹣|﹣2cs45°++（﹣）﹣2；
（2）分解因式：8a3﹣2a．
19．（5分）解方程：2x2﹣13x﹣18＝16．
20．（8分）如图，以△ABC的边BC为直径作⊙O，点A在⊙O上，AD＝AB，∠D＝30°．
（1）求证：直线AD是⊙O的切线；
（2）若直径BC＝4，求图中阴影部分的面积．
21．（10分）2020年春节我国武汉发生了“新冠状肺炎病毒”疫情，“国家有难，众志成城”，某中学在学校公众号上举办了以“疫情面前，我辈有责”为主题的视频演讲比赛．并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计（等级：A：优秀，B：良好，C：一般，D：较差）（部分信息未给出）：
请根据统计图表中的信息解答下列问题：
（1）这次共抽取了 名参加演讲比赛的学生；
（2）统计图中a＝ ，b＝ ；
（3）若该校学生共有2000人，如果都参加了演讲比赛，请你估计成绩达到优秀的有多少人？
（4）若演讲比赛成绩为A等级的学生中恰好有2名女生，其余的学生为男生，从A等级的学生中抽取两名同学参加全市演讲比赛
22．（10分）在一条笔直的公路上依次有A，C，B三地，甲、乙两人同时出发，途经C地休息1分钟，继续按原速骑行至B地，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（米）（分）之间的函数关系如图所示，请结合图象解答下列问题：
（1）请写出甲的骑行速度为 米/分，点M的坐标为 ；
（2）求甲返回时距A地的路程y与时间x之间的函数关系式（不需要写出自变量的取值范围）；
（3）请直接写出两人出发后，在甲返回A地之前，经过多长时间两人距C地的路程相等．
23．（12分）综合与实践：折纸中的数学
问题背景
在数学活动课上，老师首先将平行四边形纸片ABCD按如图①所示方式折叠，使点C与点A重合，折痕为EF．这时同学们很快证得：△AEF是等腰三角形．接下来各学习小组也动手操作起来，请你解决他们提出的问题．
操作发现
（1）“争先”小组将矩形纸片ABCD按上述方式折叠，如图②，发现重叠部分△AEF恰好是等边三角形
实践探究
（2）“励志”小组将矩形纸片ABCD沿EF折叠，如图③，使B点落在AD边上的B′处，使D点落在D′处，且B′D′过F点．试探究四边形EFGB′是什么特殊四边形？
（3）再探究：在图③中连接BB′，试判断并证明△BB′G的形状．
24．（14分）综合与探究．
如图，已知抛物线y＝ax2+bx+c（a≠0）的对称轴为x＝1，且抛物线经过A（﹣1，0）（0，﹣3）两点，与x轴交于另一点B．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上求一点M，使得|BM﹣CM|最大，并求出此时点M的坐标；
（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．
（4）在对称轴上有一点M，平面内是否存在一点N，使以B、C、M、N为顶点的四边形是菱形？若存在；若不存在，说明理由．
答案与解析
一、选择题（本大题共10小题，每小题3分，共30分）
1．【解答】解：2022的相反数是﹣2022，则﹣2020的倒数是．
故选：D．
2．【解答】解：A、不是轴对称图形，不合题意；
B、是轴对称图形，不合题意；
C、是轴对称图形，不合题意；
D、是轴对称图形，符合题意．
故选：D．
3．【解答】解：A、2a2与5a3不是同类项，不能合并；
B、2a﹣5＝≠，故选项错误；
C、（﹣）7＝1≠0，故选项错误；
D、﹣a5÷a＝﹣a2，故选项正确；
故选：D．
4．【解答】解：由于方差能反映数据的稳定性，需要比较这两名学生立定跳远成绩的方差．
故选：C．
5．【解答】解：∵AB∥CD，
∴∠1＝∠ACD＝55°，
又∵AD＝CD，
∴∠ACD＝∠CAD＝55°，
∴∠2＝180°﹣4×55°＝70°，
故选：A．
6．【解答】解：正三棱柱的左视图正三角形，
故选：C．
7．【解答】解：由点P的运动可知，当点P在GF，则对应图象为平行于t轴的线段、C错误、EF，△ABP的面积分别处于增．故D排除
故选：A．
8．【解答】解：设2米长的绳子x根，则1米长的绳子为（19﹣2x）根，
解得：，
∵x必须取整数，
∴x＝3，1，2，7，4，5，4，7，8，4，
∴有10种裁剪方案，A选项符合题意．
故选：A．
9．【解答】解：随意投掷一枚飞镖，击中黑色区域的概率是：＝．
故选：B．
10．【解答】解：由抛物线的开口向下知a＜0，
∵与y轴的交点为在y轴的正半轴上，
∴c＞0，
∵对称轴为，a＜0，
∴4a＜﹣b，
∴2a+b＜0，
故②正确；
由图可知，当x＝6时，
∴y＝4a+2b+c＜7，
故①正确；
由图可知，抛物线顶点的纵坐标大于2，
∴，
∵a＜7，
∴4ac﹣b2＜4a，
∴b2+8a＞6ac，
故③正确；
由图可知，当x＝﹣1时，
当x＝1时，y＝8，
∴a﹣b+c＜0，a+b+c＝2，
∴5a+2c＜2，
由4a+2b+c＜0，a+b+c＝5，
即4a﹣2c＜﹣6，
由4a﹣2c＜﹣7，2a+2c＜4，
∴a＜﹣1，
故④正确；
∵a+b+c＝2，a﹣b+c＜4，
∴（a+b+c）（a﹣b+c）＜0，
∴（a+c）2﹣b5＜0，
即（a+c）2＜b3，
故⑤正确；
综上可知，正确的结论有5个．
故选A．
二、填空题（本大题共7小题，每小题3分，共21分）
11．【解答】解：280万＝2800000＝2.8×106，
故答案为：2.8×103．
12．【解答】解：∵四边形ABCD是平行四边形，∠ABC＝90°，
∴四边形ABCD是矩形，
再根据现有条件无法证明平行四边形ABCD为正方形，
∴文文选择的不对，
故答案为：不对．
13．【解答】解：设扇形圆心角的度数为n，半径为r，
∵扇形的弧长为6π，面积为12π，
∴12π＝×6πr．
∵＝6π，
∴n＝270°．
故答案为：270°．
14．【解答】解：，
去分母，得2x+k＝﹣2（x﹣2）．
去括号，得2x+k＝﹣2x+5．
移项，得2x+2x＝7﹣k．
合并同类项，得4x＝6﹣k．
x的系数化为4，得x＝．
∵关于x的分式方程的解为正数，
∴x＝＞0且x＝．
∴k＜6且k≠﹣2．
故答案为：k＜6且k≠﹣6．
15．【解答】解：设点A的坐标为，
∵直线y＝﹣x与双曲线的图象交于A，
∴点B与点A关于原点对称，
∴点B的坐标为，
∵AC⊥y轴，
∴AC＝﹣m，
∴，
∴，
∴，
∴k＝﹣4，
故答案为：﹣3．
16．【解答】解：如图，
作CE⊥AB于点E，延长AB或BA到D′，连接CD′，
∵△ABC是等边三角形，AB＝8，
∴AE＝BE＝4，CE＝4，
CD′＝CD″＝13，
设BD′＝AD″＝x，
则D′E＝4+x，
在Rt△CED′中，根据勾股定理，得
（7+x）2+（4）2＝132
解得x＝5或﹣15（负值舍去）
∴BD′＝AD″＝7，
AD′＝AB+BD′＝8+3＝15．
所以AD的长为7或15．
故答案为7或15．
17．【解答】解：如图，连接OO2，则OO2与AB交于点O5，
在正方形AOBO2中，顶点A的坐标为A（0，
∴OA＝OB＝6，AO1＝BO1，
∴点B（5，0），
∴O1（3，1），
同理O2（2，2），O3（3，2），O4（8，4），O5（10，5），O6（14，8）……
由此发现，下标为偶数的点的纵坐标为加1，
∴下标为偶数的点在直线上，
∴点O2020的纵坐标为21010，
∴，
∴x＝21011﹣2，
∴点O2020的坐标为（21011﹣1，21010）．
故答案为（21011﹣1，21010）．
三.解答题（本大题共6个小题，共69分。解答应写出必要的文字说明，证明过程或演算步骤）
18．【解答】解：（1）原式＝1+﹣6﹣2×+9
＝4+﹣1﹣+9
＝5+2；
（2）原式＝7a（4a2﹣4）
＝2a（2a+6）（2a﹣1）．
19．【解答】解：方程化为2x2﹣13x﹣34＝5，
∵a＝2，b＝﹣13，
∴Δ＝b2﹣4ac＝（﹣13）2﹣4×2×（﹣34）＝441＞0，
∴方程有两个不相等的实数根，
，
即，x2＝﹣2．
20．【解答】（1）证明：连接OA，则∠COA＝2∠B，
∵AD＝AB，
∴∠B＝∠D＝30°，
∴∠COA＝60°，
∴∠OAD＝180°﹣60°﹣30°＝90°，
∴OA⊥AD，
即CD是⊙O的切线；
（2）解：∵BC＝4，
∴OA＝OC＝7，
在Rt△OAD中，OA＝2，
∴OD＝2OA＝6，AD＝2，
所以S△OAD＝OA•AD＝＝2，
因为∠COA＝60°，
所以S扇形COA＝＝π，
所以S阴影＝S△OAD﹣S扇形COA＝2﹣．
21．【解答】解：（1）这次共抽取的参加演讲比赛的学生人数为：10÷20%＝50（名），
故答案为：50；
（2）∵a%＝20÷50×100%＝40%，
∴a＝40，
∵m＝50×10%＝5，
∴n＝50﹣5﹣20﹣10＝15，
∴b%＝15÷50×100%＝30%，
∴b＝30，
故答案为：40，30；
（3）2000×10%＝200（人），
答：估计成绩达到优秀的约有200人；
（4）∵A等级的学生2名学生中恰好有2名女生，
∴男生有3名，
画树状图如下：
共有20种等可能的结果，其中抽中一名男生和一名女生的结果有12种，
∴抽中一名男生和一名女生的概率为＝．
22．（1）请写出甲的骑行速度为 240 米/分，点M的坐标为 （6，1200） ；
（2）求甲返回时距A地的路程y与时间x之间的函数关系式（不需要写出自变量的取值
【解答】解：（1）由题意得：甲的骑行速度为：＝240（米/分），
240×（11﹣4）÷2＝1200（米），
因为甲往返总时间为11分，中间休息一分钟，
则点M的坐标为（6，1200），
故答案为：240，（5；
（2）设MN的解析式为：y＝kx+b（k≠0），
∵y＝kx+b（k≠0）的图象过点M（8，1200），0），
∴，
解得，
∴直线MN的解析式为：y＝﹣240x+2640；
即甲返回时距A地的路程y与时间x之间的函数关系式：y＝﹣240x+2640；
（3）设甲返回A地之前，经过x分两人距C地的路程相等（x≤6），
乙的速度：1200÷20＝60（米/分），
如图1所示：∵AB＝1200，AC＝1020，
∴BC＝1200﹣1020＝180，
分7种情况：
①当0＜x≤3时，1020﹣240x＝180﹣60x，
x＝＞3，
此种情况不符合题意；
②当3＜x＜﹣1时，甲、乙都在A，
∴1020﹣240x＝60x﹣180，
x＝4，
此种情况符合题意；
③当＜x＜6时、C之间、C之间，
∴240（x﹣6）﹣1020＝60x﹣180，
x＝6，
此种情况不符合题意；
④当x＝6时，甲到B地，
乙距C地的距离：4×60﹣180＝180（米），
即x＝6时两人距C地的路程相等，
⑤当x＝8时，甲到B地返回时，
乙距C地的距离：2×60﹣180＝300（米），
即x＝8时两人距C地的路程相等，
综上所述，在甲返回A地之前．
23．【解答】解：（1）矩形ABCD的长、宽之比应是．
证明：设BE＝a，
∵△AEF等边三角形，
∴∠EAF＝60°，
∵四边形ABCD为矩形，
∴∠BAD＝∠ABE＝90°，∠BAE＝∠BAD﹣∠EAF＝30°．
在Rt△ABE中，∠ABE＝90°，BE＝a，
∴，，
∵AE＝EC，∴BC＝BE+EC＝3a，
∴．
（2）四边形EFGB′是平行四边形．
证明：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠B′EF＝∠BFE，∠EB′F＝∠GFB′．
由翻折的特性可知：∠BFE＝∠B′FE，∠DB′G＝∠FB′G，
∴∠B′EF＝∠B′FE，∠FB′G＝∠FGB′，
又∵∠EB′F＝∠GFB′，
∴∠B′FE＝∠FB′G，
∴EF∥B′G，
又∵B′E∥FG，
∴四边形EFGB′是平行四边形．
（3）△BB′G为直角三角形．
证明：连接BB′交EF于点M，如图所示．
∵AD∥BC，
∴∠EB′B＝∠FBB′，
∵BF＝B′F，
∴∠FBB′＝∠FB′B，
∴∠EB′B＝∠FB′B．
∵∠B′EF＝∠B′FE，
∴△B′EF为等腰三角形，
∴B′M⊥EF，
∴∠BMF＝90°．
∵EF∥B′G，
∴∠BB′G＝∠BMF＝90°，
∴△BB′G为直角三角形．
24．【解答】解：（1）由A、B点关于x＝1对称，0），得 ，3）．
将A、B、C点坐标代入抛物线解析式，
得，
解得 ，
这条抛物线所对应的函数关系式为y＝x7﹣2x﹣3；
（2）如图，连接AC并延长交抛物线的对称轴于M，A，
则AM＝BM，
∴|BM﹣CM|＝|AM﹣CM|＝AC，此时|BM﹣CM|最大，
∵A（﹣2，0），﹣3），
设直线AC为y＝kx﹣2，
∴﹣k﹣3＝0，
解得：k＝﹣2，
∴直线AC为：y＝﹣3x﹣3，
当x＝3时，
y＝﹣3﹣3＝﹣6，
∴M（1，﹣6）；
（3）∵抛物线的对称轴为直线x＝6，
设P点坐标为（1，m）
过P点作PD⊥y轴于D点，由OB＝OC，
得∠OBC＝∠OCB＝45°．
∵∠PCB＝90°，
∴∠OCB+∠PCD＝90°，
∴∠PCD＝∠DPC＝45°．
∴PD＝CD，即﹣3﹣m＝4，
解得m＝﹣4，
∴P（1，﹣8）；
（4）存在，理由如下：
设M（1，n），0），﹣2），
∴BC2＝32+32＝18，MC5＝12+（n+3）2，MB2＝（6﹣3）2+n4＝n2+4，
①如图：
当MB为对角线时，则CB＝CM，
∴7+（n+3）2＝18，
解得：，
∴当时，由平移的性质可得：，
当时，由平移的性质可得：，
当BC为对角线时，则MC＝MB，
∴1+（n+3）4＝n2+4，
解得：n＝﹣5，
∴M（1，﹣1），﹣7），
如图，当MC为对角线时，
∴n2+4＝18，
解得：，
当时，由平移的性质可得：，
当，由平移的性质可得：，
综上：或或N（2或．等级
人数
A
m
B
20
C
n
D
10