2024年新高考数学一轮复习题型归类与强化测试专题07函数的单调性与最大小值（学生版）

这是一份2024年新高考数学一轮复习题型归类与强化测试专题07函数的单调性与最大小值（学生版），共12页。试卷主要包含了【知识梳理】，【题型归类】，【培优训练】，【强化测试】等内容，欢迎下载使用。
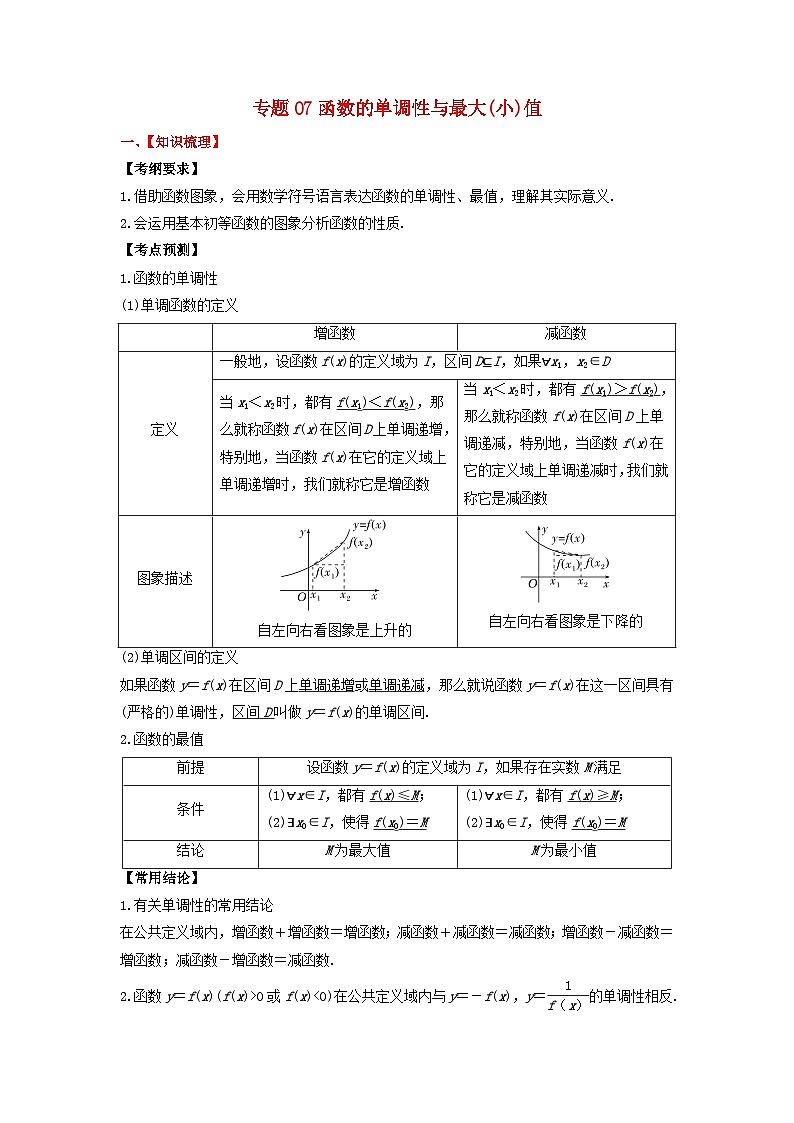
【考纲要求】
1.借助函数图象，会用数学符号语言表达函数的单调性、最值，理解其实际意义.
2.会运用基本初等函数的图象分析函数的性质.
【考点预测】
1.函数的单调性
(1)单调函数的定义
(2)单调区间的定义
如果函数y＝f(x)在区间D上单调递增或单调递减，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间D叫做y＝f(x)的单调区间.
2.函数的最值
【常用结论】
1.有关单调性的常用结论
在公共定义域内，增函数＋增函数＝增函数；减函数＋减函数＝减函数；增函数－减函数＝增函数；减函数－增函数＝减函数.
2.函数y＝f(x)(f(x)>0或f(x)0)在(0，＋∞)上的单调性．
【典例3】判断并证明函数f(x)＝ax2＋eq \f(1,x)(其中10时，f(x)1时，f(x)>0，且对于任意的正数x，y都有f(xy)＝f(x)＋f(y)．
(1)证明：函数f(x)在定义域上是单调增函数；
(2)如果feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))＝－1且f(x)－feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x－2)))≥2，求x的取值范围．
三、【培优训练】
【训练一】函数g(x)＝ax＋2(a>0)，f(x)＝x2－2x，对∀x1∈[－1,2]，∃x0∈[－1,2]，使g(x1)＝f(x0)成立，则a的取值范围是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,3))) B．[1,2)
C.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2))) D.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,3)，＋∞))
【训练二】已知函数f(x)＝x2＋lnx－ax在(0，1)上是增函数．
(1)求a的取值范围；
(2)在(1)的结论下，设g(x)＝e2x＋eq \b\lc\|\rc\|(\a\vs4\al\c1(ex－a))，x∈[0，ln3]，求函数g(x)的最小值．
【训练三】已知函数f(x)＝2 020x＋ln(eq \r(x2＋1)＋x)－2 020－x＋1，则不等式f(2x－1)＋f(2x)>2的解集为____________．
【训练四】已知定义在区间(0，＋∞)上的函数f(x)是增函数，f(1)＝0，f(3)＝1.
(1)解不等式00，试确定a的取值范围.
四、【强化测试】
【单选题】
1. 下列函数中，在区间(0，＋∞)上单调递增的是( )
A．y＝ln(x＋2) B．y＝－eq \r(x＋1)
C．y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x D．y＝x＋eq \f(1,x)
2. 函数f(x)＝eq \f(x,1－x)在( )
A．(－∞，1)∪(1，＋∞)上是增函数
B．(－∞，1)∪(1，＋∞)上是减函数
C．(－∞，1)和(1，＋∞)上是增函数
D．(－∞，1)和(1，＋∞)上是减函数
3. 设a∈R，函数f(x)在R上是增函数，则( )
A．f(a2＋a＋2)>f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7,4))) B．f(a2＋a＋2)－1的实数x的取值范围是( )
A．(3，＋∞) B．(－∞，3)
C．[2,3) D．[0,3)
6. 函数f(x)＝－x＋eq \f(1,x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－2，－\f(1,3)))上的最大值是( )
A．eq \f(3,2) B．－eq \f(8,3)
C．－2 D．2
7. 函数y＝f(x)在[0，2]上单调递增，且函数f(x)的图象关于直线x＝2对称，则下列结论成立的是( )
A．f(1)