2024年新高考数学一轮复习知识梳理与题型归纳第47讲直线与圆圆与圆的位置关系（学生版）

这是一份2024年新高考数学一轮复习知识梳理与题型归纳第47讲直线与圆圆与圆的位置关系（学生版），共6页。试卷主要包含了直线与圆的位置关系，圆与圆的位置关系等内容，欢迎下载使用。

知识梳理
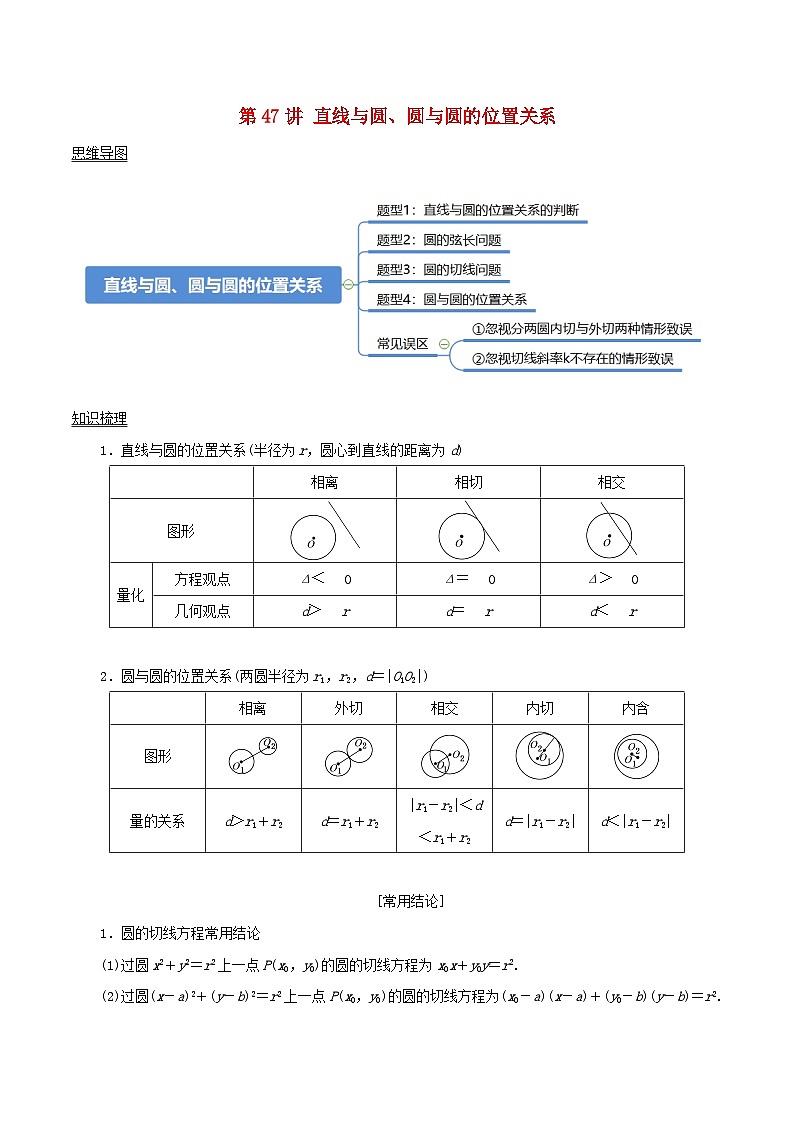
1．直线与圆的位置关系(半径为r，圆心到直线的距离为d)
2．圆与圆的位置关系(两圆半径为r1，r2，d＝|O1O2|)
[常用结论]
1．圆的切线方程常用结论
(1)过圆x2＋y2＝r2上一点P(x0，y0)的圆的切线方程为x0x＋y0y＝r2.
(2)过圆(x－a)2＋(y－b)2＝r2上一点P(x0，y0)的圆的切线方程为(x0－a)(x－a)＋(y0－b)(y－b)＝r2.
(3)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.
2．圆系方程
(1)同心圆系方程：(x－a)2＋(y－b)2＝r2(r＞0)，其中a，b是定值，r是参数；
(2)过直线Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0交点的圆系方程：x2＋y2＋Dx＋Ey＋F＋λ(Ax＋By＋C)＝0(λ∈R)；
(3)过圆C1：x2＋y2＋D1x＋E1y＋F1＝0和圆C2：x2＋y2＋D2x＋E2y＋F2＝0交点的圆系方程：x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0(λ≠－1)(该圆系不含圆C2，解题时，注意检验圆C2是否满足题意，以防漏解)．
题型归纳
题型1 直线与圆的位置关系的判断
【例1-1】直线kx﹣y+1＝0与圆x2+y2+2x﹣4y+1＝0的位置关系是（ ）
A．相交B．相切C．相离D．不确定
【例1-2】若无论实数a取何值时，直线ax+y+a+1＝0与圆x2+y2﹣2x﹣2y+b＝0都相交，则实数b的取值范围．（ ）
A．（﹣∞，2）B．（2，+∞）C．（﹣∞，﹣6）D．（﹣6，+∞）
【例1-3】已知圆O：x2+y2＝1上恰有两个点到直线l：y＝kx+1的距离为，则直线l的倾斜角的取值范围为（ ）
A．[0，）∪（，）B．[0，）∪（，π）
C．（，）∪（，）D．（，）∪（，π）
【跟踪训练1-1】方程（a﹣1）x﹣y+2a+1＝0（a∈R）所表示的直线与圆（x+1）2+y2＝25的位置关系是（ ）
A．相离B．相切C．相交D．不能确定
【跟踪训练1-2】若直线l：y+1＝k（x+）与圆C：x2+y2＝1有公共点，则实数k的最大值为（ ）
A．B．1C．D．
【跟踪训练1-3】若直线y＝kx+1与圆（x﹣2）2+y2＝4相交，且两个交点位于坐标平面的同一象限，则k的取值范围是（ ）
A．（0，）B．（﹣，）C．（0，）D．（﹣，）
【名师指导】
判断直线与圆的位置关系的一般方法
题型2 圆的弦长问题
【例2-1】直线y＝x+1被圆x2+y2＝4截得的弦长为（ ）
A．B．2C．D．
【例2-2】设直线y＝x+2a与圆C：x2+y2﹣2ay﹣2＝0相交于A，B两点，若|AB|＝2，则圆C的面积为（ ）
A．4πB．6πC．8πD．π
【跟踪训练1-1】已知圆x2+y2﹣2x+2y+a＝0截直线x+y﹣2＝0所得弦的长度为4，则实数a的值是（ ）
A．﹣8B．﹣6C．﹣5D．﹣4
【跟踪训练1-2】已知圆C：（x﹣1）2+（y﹣2）2＝25，直线l：（2m+1）x+（m+1）y﹣7m﹣4＝0，则直线l被圆C截得的弦长的最小值为（ ）
A．2B．4C．6D．8
【名师指导】
有关弦长问题的2种求法
题型3 圆的切线问题
【例3-1】已知点P（1，﹣2），点M（3，1），圆C：（x﹣1）2+（y﹣2）2＝4．
①求过点P的圆C的切线方程；
②求过点M的圆C的切线方程．
【跟踪训练3-1】过点P（2，﹣1）的直线与圆C：（x+1）2+（y﹣1）2＝5相切，则切线长为（ ）
A．B．C．D．
【跟踪训练3-2】过原点O作圆C：x2+y2+4x+4y+5＝0的两条切线，设切点分别为A，B，则直线AB的方程为（ ）
A．2x+2y﹣5＝0B．4x+4y﹣5＝0C．2x+2y+5＝0D．4x+4y+5＝0
【跟踪训练3-3】已知圆C经过M（3，0），N（2，1）两点，且圆心在直线l：2x+y﹣4＝0上．
（1）求圆C的方程；
（2）从y轴上一个动点P向圆C作切线，求切线长的最小值及对应切线方程．
【名师指导】
1．求过圆上的一点(x0，y0)的切线方程的方法
先求切点与圆心连线的斜率k，若k不存在，则结合图形可直接写出切线方程为y＝y0；若k＝0，则结合图形可直接写出切线方程为x＝x0；若k存在且k≠0，则由垂直关系知切线的斜率为－eq \f(1,k)，由点斜式可写出切线方程．
2．求过圆外一点(x0，y0)的圆的切线方程的2种方法
题型4 圆与圆的位置关系
【例4-1】若圆C1：x2+y2＝4与圆C2：x2+y2﹣6x﹣8y+m＝0外切，则实数m＝（ ）
A．﹣24B．﹣16C．24D．16
【例4-2】已知圆的圆心到直线x﹣y﹣2＝0的距离为，则圆C1与圆的位置关系是（ ）
A．相交B．内切C．外切D．相离
【跟踪训练4-1】已知圆C1：x2+y2+2x+8y﹣8＝0和圆C2：（x﹣5）2+（y﹣4）2＝25，则圆C1与圆C2的位置关系为（ ）
A．外切B．内切C．相交D．相离
【跟踪训练4-2】已知圆C1：x2+y2+2ax﹣9+a2＝0和圆C2：x2+y2﹣2by﹣1+b2＝0外切（其中a，b∈R），则a+b的最大值为（ ）
A．4B．4C．8D．4
【名师指导】
圆与圆位置关系问题的解题策略
(1)判断两圆的位置关系时常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法．
(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差消去x2，y2项得到．相离
相切
相交
图形
量化
方程观点
Δeq \a\vs4\al(＜)0
Δeq \a\vs4\al(＝)0
Δeq \a\vs4\al(＞)0
几何观点
deq \a\vs4\al(＞)r
deq \a\vs4\al(＝)r
deq \a\vs4\al(＜)r
相离
外切
相交
内切
内含
图形
量的关系
d＞r1＋r2
d＝r1＋r2
|r1－r2|＜d＜r1＋r2
d＝|r1－r2|
d＜|r1－r2|
几何法
圆心到直线的距离与圆半径比较大小，即可判断直线与圆的位置关系．这种方法的特点是计算量较小
代数法
将直线方程与圆方程联立方程组，再将二次方程组转化为一元二次方程，该方程解的情况即对应直线与圆的位置关系．这种方法具有一般性，适合于判断直线与圆锥曲线的位置关系
几何法
直线被圆截得的半弦长eq \f(l,2)，弦心距d和圆的半径r构成直角三角形，即r2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(l,2)))2＋d2
代数法
联立直线方程和圆的方程，消元转化为关于x的一元二次方程，由根与系数的关系即可求得弦长|AB|＝eq \r(1＋k2)·|x1－x2|＝eq \r(1＋k2)eq \r(x1＋x22－4x1x2)或|AB|＝eq \r(1＋\f(1,k2))·|y1－y2|＝eq \r(1＋\f(1,k2))eq \r(y1＋y22－4y1y2)
几何法
当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即kx－y＋y0－kx0＝0.由圆心到直线的距离等于半径，即可求出k的值，进而写出切线方程
代数法
当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即y＝kx－kx0＋y0，代入圆的方程，得到一个关于x的一元二次方程，由Δ＝0，求得k，切线方程即可求出