

陕西省宝鸡市凤翔区2023-2024学年八年级上学期期末质量检测数学试卷(含答案)
展开八年级数学试题(卷)
一、选择题(每小题3分,共24分.)
1.方程,是二元一次方程的有()
A.1个B.2个C.3个D.4个
2.下列实数中是无理数的是()
A.B.3.14C.D.0
3.下列运算正确的是()
A.B.C.D.
4.平面直角坐标系内,点位于()
A.第一象限B.第二象限C.第三象限D.第四象限
5.下列命题是真命题的是()
A.两条直线同时被第三条直线所截,同位角相等.B.相等的角是对顶角
C.三角形的外角大于任一内角D.直角三角形的两锐角互余
6.若二次根式有意义,则x的值不可以是()
A.3B.2C.1D.0
7.中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无入乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为()
A.B.C.D.
8.如图,直线与直线相交于点,则关于x,y的方程组的解为()
A.B.C.D.
二、填空题(每小题3分,共15分)
9.在中,,求证,用反证法证明第一步假设_____________.
10.甲、乙两队参加,“传承红色基因,推动绿色发展”为主题的合唱比赛,每队均由20名队员组成.其中两队队员的平均身高为,身高的方差分别为.如果单从队员的身高考虑,你认为演出形象效果较好的队是_____________.(填“甲队”或“乙队”)
11.已知点都在直线上,则_____________(填“>”“<”或“=”).
12.如图,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当时,则阴影部分的面积为_____________.
13.如图,在中,,和的平分线交于点,得和的平分线交于点,得,…,和的平分线交于点,则_____________度.
三、解答题(本大题共13个小题,共81分)
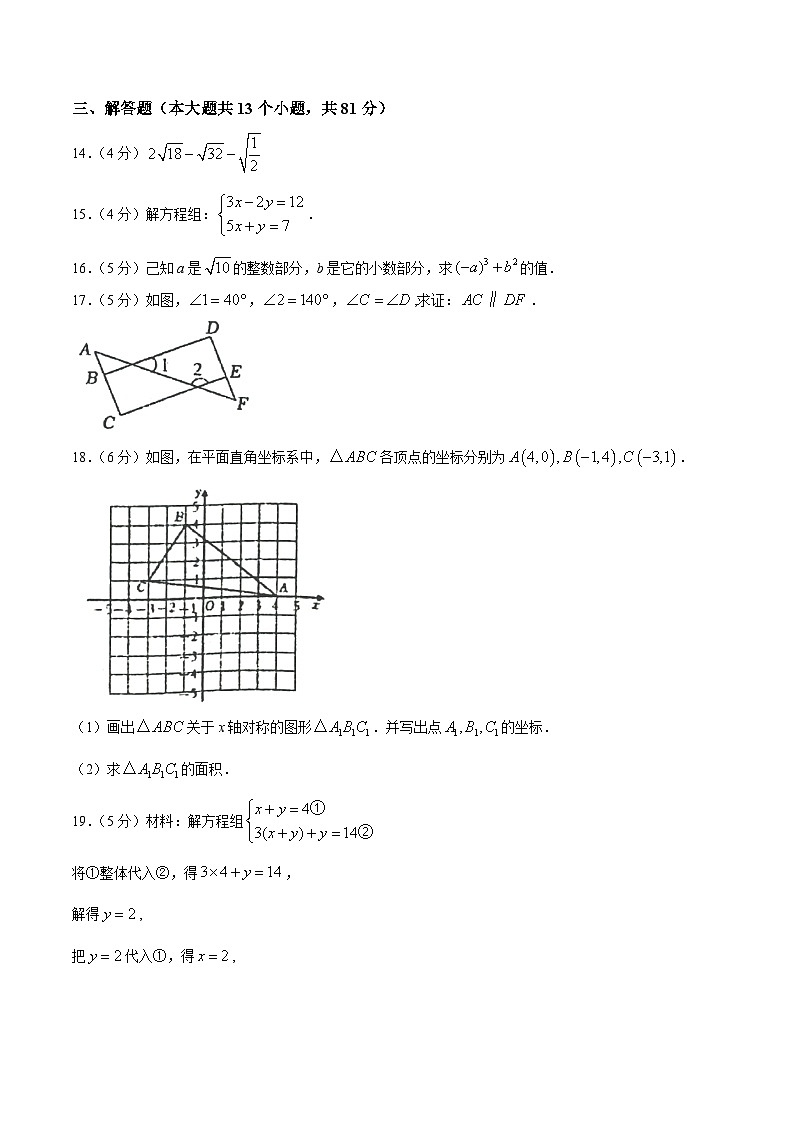
14.(4分)
15.(4分)解方程组:.
16.(5分)己知a是的整数部分,b是它的小数部分,求的值.
17.(5分)如图,,,,求证:.
18.(6分)如图,在平面直角坐标系中,各顶点的坐标分别为.
(1)画出关于x轴对称的图形.并写出点的坐标.
(2)求的面积.
19.(5分)材料:解方程组
将①整体代入②,得,
解得,
把代入①,得,
所以
这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答,请解方程组
20.(5分)某消防队进行消防演练,在模拟现场,有一建筑物发生了火灾,消防车到达后,发现离建筑物的水平距离最近为12米,即米,此时建筑物中距地面12.8米高的P处有一被困人员需要救援,已知消防云梯的车身高是3.8米.为此消防车的云梯至少应伸长多少米?
21.(6分)如图,在中,,,,求的度数.
22.(7分)水龙头关闭不严会造成滴水,小明用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的容器内盛水量与滴水时间的函数关系图象,请结合图象解答下列问题.
图1图2
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?
23.(7分)为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元.
(1)求文具袋和圆规的单价.
(2)学校准备购买文具袋20个,圆规100个,文具店给出两种优惠方案:
方案一:每购买一个文具袋赠送1个圆规.
方案二:购买10个以上圆规时,超出10个的部分按原价的八折优惠,文具袋不打折.学校选择哪种方案更划算?请说明理由.
24.(7分)某校组织全体1500名学生参加“强国有我”读书活动,要求每人必读本书,活动结束后从各年级学生中随机抽查了若干名学生了解读书数量情况,并根据A:1本;B:2本;C:3本;D:4本,四种类型的人数绘制了不完整的条形统计图(图1)和扇形统计图(图2).请根据统计图解答下列问题:
图1图2
(1)写出这次调查中D类型学生人数并补全条形统计图;
(2)直接写出被调查学生读书数量的众数和中位数;
(3)求被调查学生读书数量的平均数,并估计全校1500名学生共读书多少本?
25.(8分)如图,己知直线与直线交于点A.
(1)求点A和点C的坐标;
(2)在y轴上是否存在一点P,使得?若存在,请求出P点的坐标;若不存在,请说明理由.
26.(12分)如图,将一副三角板中的两个直角顶点C叠放在一起,其中,,.
备用图
【观察猜想】(1)与的数量关系是_____________;与的数量关系是_____________;
【类比探究】(2)若保持三角板不动,绕直角顶点C顺时针转动三角板,试探究当等于多少度时,画出图形并简要说明理由;
【拓展应用】(3)若,求的度数;并直接写出此时与的位置关系.
2023-2024学年第一学期八年级数学题参考答案
一、选择题(每小题3分,共24分)
1.B 2.C 3.D 4.B 5.D 6.A 7.A 8.A
二、填空题(每小题3分,共15分)
9.∠B=∠C; 10.乙队; 11.<;
12.24; 13.
三、解答题(本大题共13个小题,共81分)
14.(4分)解:(1)原式
;
15.(4分)原方程组的解为
16.(5分)解:,
,
∴原式
.
17.(5分)证明:∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠D=∠CEF,
∵∠C=∠D,
∴∠CEF=∠C,
∴AC∥DF.
18.(6分)解:(1)如图,△AB'C'即为所求;
A'(4,0),B'(﹣1,﹣4),C'(﹣3,﹣1).
(2)△AB'C'的面积为11.5.
19.(5分)解:(1)由①得:x﹣y=1③,
将③代入②得:4×1﹣y=5,
解得:y=﹣1,
将y=﹣1代入①得:x﹣(﹣1)﹣1=0,
解得:x=0,
∴方程组的解为.
故答案为:;
20.(5分)解:由题意可知:AB=CD=3.8米,AD=12米,PC=12.8米,∠ADP=90°,
∴PD=PC﹣CD=9米,
在Rt△ADP中,由勾股定理得,米,
答:此消防车的云梯至少应伸长15米.
21.(5分)解:∵∠AEB=∠C+∠CAE,∠C=40°,∠CAE=20°,
∴∠AEB=60°.
∵∠CBD=30°,
∴∠BFE=180°﹣30°﹣60°=90°,
∴∠AFB=180°﹣∠BFE=90°.
22.(6分)解:(1)根据图象可知,t=0时,w=0.3,即容器内原有水0.3升;
(2)设w与t之间的函数关系式为y=kt+b,
将(0,0.3),(1.5,0.9)代入,
得:,
解得:,
故w与t之间的函数关系式为w=0.4t+0.3;
当t=24时,w=0.4×24+0.3=9.9(升),
∴这种滴水状态下一天的滴水量是9.9﹣0.3=9.6升,
故在这种滴水状态下一天的滴水量是9.6升.
23.(7分)解:(1)设文具袋的单价为x元,圆规的单价为y元.
依题意,得
解得
答:文具袋的单价为15元,圆规的单价为3元.
(2)选择方案一的总费用为20×15+3×(100﹣20)=540(元),
选择方案二的总费用为20×15+10×3+3×80%×(100﹣10)=546(元),
∵540<546,
∴选择方案一更划算.
24.(7分)解:(1)这次调查一共抽查学生人数为80÷40%=200(人),
D类人数=200×10%=20(人);
补全条形统计图如下:
(2)被调查学生读书数量的众数为2本,中位数为2本;
(3)被调查学生读书数量的平均数为:(本),
2.3×1500=3450(本),
答:估计全校1500名学生共读书3450本.
25.(10分)解:(1)联立方程组,解得,
∴A点坐标为(2,2);
(2)直线,令y=0,解得x=-2,∴C(﹣2,0)
直线AB:y=﹣x+4,令y=0,解得x=4,∴B(4,0),
设P(0,m),
∵直线AB:y=﹣x+4与x轴的交点B(4,0),S△PBC=S△ABC,
,
∴m=±2,
∴点P的坐标为(0,2)或(0,﹣2).
26.(12分)
解:(1)∵∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,
∴∠BCD=∠ACE;
∵∠BCE=∠ACB+∠ACE=90°+∠ACE,
∴∠BCE+∠ACD=90°+∠ACE+∠ACD=90°+90°=180°,
∴∠BCE+∠ACD=180°.故答案为:∠BCD=∠ACE;∠BCE+∠ACD=180°;
(2)分两种情况:
①如图1所示,当CE∥AB时,∠ACE=∠A=30°,
∴∠ACD=∠DCE﹣∠ACE=90°﹣30°=60°.
②如图2所示,当CE∥AB时,∠BCE=∠B=60°,
∴∠ACD=360°﹣∠ACB﹣∠BCE﹣∠DCE=360°﹣90°﹣60°﹣90°=120°.
综上所述,当∠ACD等于60°或120°时,CE∥AB;
(3)设∠ACD=α,则∠BCE=3α.
由(1)可知,∠BCE+∠ACD=180°,
∴3α+α=180°,
∴α=45°,即∠ACD=45°,
此时DE⊥AC或DE∥AC.
陕西省宝鸡市凤翔区2023-2024学年上学期八年级数学期末试题(图片版,含答案): 这是一份陕西省宝鸡市凤翔区2023-2024学年上学期八年级数学期末试题(图片版,含答案),文件包含八年级数学期末试题参考答案docx、八年级数学期末考试试题pdf等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
陕西省宝鸡市凤翔县2022届九年级上学期期末质量检测数学试卷(含答案): 这是一份陕西省宝鸡市凤翔县2022届九年级上学期期末质量检测数学试卷(含答案),共9页。试卷主要包含了本试题共6页.测试时间, 方程经配方后,可化为.等内容,欢迎下载使用。
2023-2024学年陕西省宝鸡市凤翔区九年级上学期期中数学质量检测模拟试题(含解析): 这是一份2023-2024学年陕西省宝鸡市凤翔区九年级上学期期中数学质量检测模拟试题(含解析),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












