新高考数学二轮复习专题3 第2讲　空间点、线、面的位置关系（练·教师版）【新教材·新高考】

展开

这是一份新高考数学二轮复习专题3 第2讲　空间点、线、面的位置关系（练·教师版）【新教材·新高考】，文件包含第2讲空间点线面的位置关系练·教师版新教材地区专用docx、第2讲空间点线面的位置关系练·学生版新教材地区专用docx等2份试卷配套教学资源，其中试卷共28页，欢迎下载使用。

高考数学一轮靠老师勤奋、学生努力；高考数学二轮主要看老师的把握水平(课标、考纲)，研究水平(选题、集体备课)，辅导水平(课堂辅导，课后个辅)。
二、高考数学二轮复习要注意明确两个做法：抓审题，抓个辅
抓审题：让学生说出来，让思维呈现出来。充分调动学生审题、变题能力;
抓个辅：教师要有个辅学生问题清单，让辅导有针对性;个辅全程性，个辅不只在课后，课堂个辅也是关键。
三、高考数学二轮复习要注意坚持三个过关：必须记忆过关;必须限时过关;必须心理过关
1、高考数学每节课必须花5分钟过关记忆性知识。
2、学生训练最大的状态就是能限时过关，应试能力也是数学解题能力，极大限度地减少题海战术。
3、学生最大的障碍就是就是心理问题。
四、高三数学二轮复习要注意避免四个重复：
重复一轮复习老路；重复成套试题训练；重复迷信名校资料；重复个人喜好方向。

第2讲空间点、线、面的位置关系（练·教师版）
一、单项选择题
1．（2021·吉林长春市高三（理））给出下列命题：
①若的三条边所在直线分别交平面于三点，则三点共线；
②若直线是异面直线，直线是异面直线，则直线是异面直线；
③若三条直线两两平行且分别交直线于三点，则这四条直线共面；
④对于三条直线，若，，则.
其中所有真命题的序号是（）
A．①②B．①③C．③④D．②④
【答案】B
【解析】对于①中，若的三条边所在直线分别交平面于三点，
可得且平面，所以三点必在两平面的交线上，
所以三点共线，所以①正确；
对于②中，若直线是异面直线，直线是异面直线，则直线可能相交，平行或异面直线，所以②错误；
对于③中，若三条直线两两平行且分别交直线于三点，由公理3可得这四条直线共面，所以③正确；
对于④中，例如：若是过长方体一顶点的三条棱，则满足若，，此时与相交，所以④错误.
其中所有真命题的序号是①③.故选B.
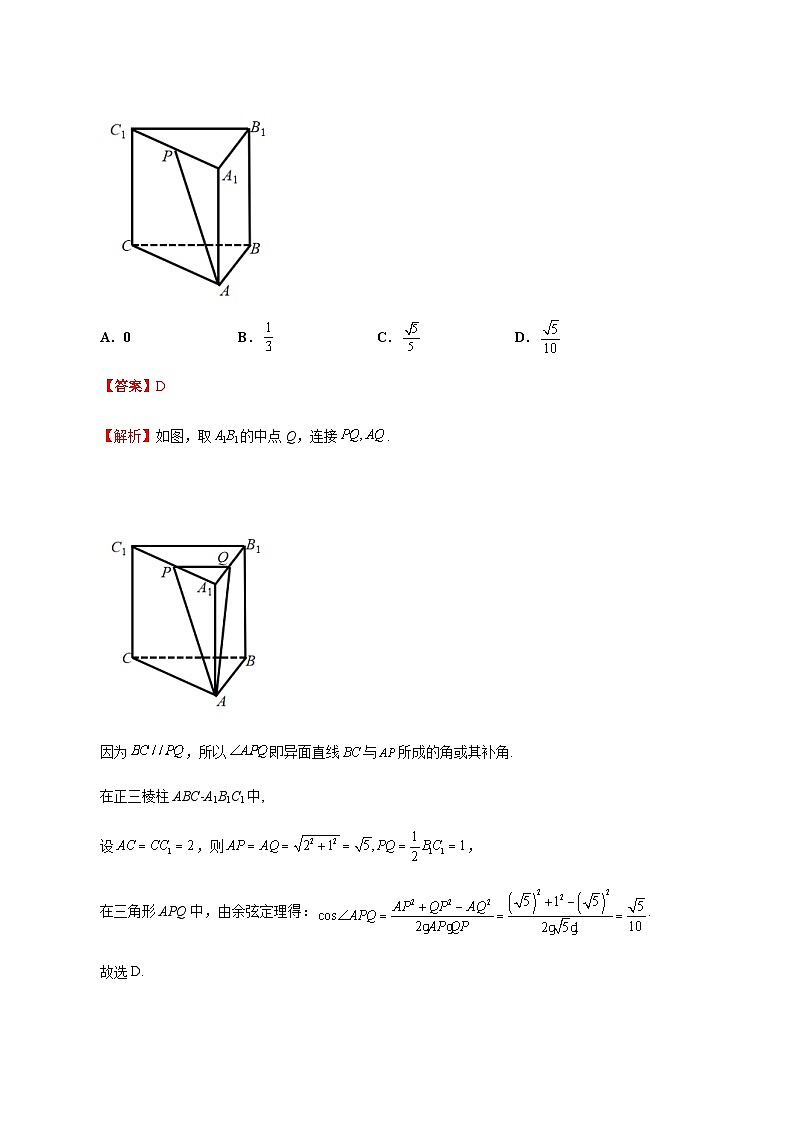
2．（2021·贵州高三月考（文））如图，在正三棱柱ABC-A1B1C1中，AC=CC1，P是A1C1的中点，则异面直线BC与AP所成角的余弦值为（）
A．0B．C．D．
【答案】D
【解析】如图，取的中点Q，连接.
因为，所以即异面直线与所成的角或其补角.
在正三棱柱ABC-A1B1C1中,
设，则，
在三角形APQ中，由余弦定理得：.
故选D.
3．已知如图，在棱长为2的正方体中，过且与平行的平面交于点，则（）
A．2B．C．D．1
【答案】D
【解析】连接交于，过作交于，则是的中点，如下图示，
∵面，面，
∴面，即为所求的点，又在△中，，而，
∴.故选D.
4．（2021·陕西高三模拟（文））设、、为平面，、、为直线，则的一个充分条件是（）
A．，，B．，，
C．，，D．，，
【答案】D
【解析】选项A：若，，，则由线面位置关系知，直线与平面可相交，可平行，也可以是直线在平面内，故选项A错误；
选项B：若，，，则由线面位置关系知，直线与平面可相交，也可平行，故选项B错误；
选项C：若，，，则由线面位置关系知，直线与平面可相交，可平行，也可以是直线在平面内，故选项C错误；
选项D：若，，则由线面垂直的性质得，又，所以，故选项D正确.故选D.
5．如图，在正方体中，为棱的中点，为底面内一点，则“为棱的中点”是“平面”的（）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【解析】取的中点，为棱的中点，，面，面，所以面
又，同理可证面，又，面，所以平面平面，所以在线段上时均能使平面
所以“为棱的中点”是“平面”的充分不必要条件.故选A.
6．（2021·江西上饶市高三三模（理））在正方体中，点G是线段上的一点，且，则（）
A．B．
C．D．点G为线段上任意一点
【答案】D
【解析】在正方体中，如图所示，
∵平面，∴，
又∵，平面，平面，
∴平面，∴，
同理可得，
而平面，平面，
∴平面，又∵平面，∴，
所以点G为线段上任意一点.故选D.
二、多项选择题
7．如图，以等腰直角三角形ABC的斜边BC上的高AD为折痕，翻折△ABD和△ACD，使得平面ABD⊥平面ACD.下列结论正确的是( )
A．BD⊥AC B．△BAC是等边三角形
C．三棱锥D－ABC是正三棱锥 D．平面ADC⊥平面ABC
【答案】ABC
【解析】由题意易知，BD⊥平面ADC，又AC⊂平面ADC，故BD⊥AC，A中结论正确；设等腰直角三角形ABC的腰为a，则BC＝eq \r(2)a，由A知BD⊥平面ADC，CD⊂平面ADC，∴BD⊥CD，又BD＝CD＝eq \f(\r(2),2)a，∴由勾股定理得BC＝eq \r(2)×eq \f(\r(2),2)a＝a，∴AB＝AC＝BC，则△BAC是等边三角形，B中结论正确；易知DA＝DB＝DC，又由B可知C中结论正确，D中结论错误．
8．列四个命题中：①存在这样的四面体，使；②存在这样的四面体，使；③存在这样的四面体，使；④存在这样的四面体，使，其中真命题是（）
A．①B．②C．③D．④
【答案】ABC
【解析】对于①，存在这样的四面体，使，如图所示，故①正确；
对于②，存在这样的四面体，使，如图所示，故②正确；
对于③，存在这样的四面体，使，故③正确；
对于④，若，则A，B，C，D四点共面，故④错误，故真命题是①②③，故选ABC
9．如图，已知四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD＝NB＝1，E为MC的中点，则下列结论正确的是( )
A．平面BCE⊥平面ABN B．MC⊥AN
C．平面CMN⊥平面AMN D．平面BDE∥平面AMN
【答案】ABD
【解析】如图，分别过A，C作平面ABCD的垂线AP，CQ，使得AP＝CQ＝1，
连接PM，PN，QM，QN，将几何体补成棱长为1的正方体．
∴BC⊥平面ABN，
又BC⊂平面BCE，
∴平面BCE⊥平面ABN，故A正确；
连接PB，则PB∥MC，显然PB⊥AN，
∴MC⊥AN，故B正确；
取MN的中点F，连接AF，CF，AC.
∵△AMN和△CMN都是边长为eq \r(2)的等边三角形，
∴AF⊥MN，CF⊥MN，
∴∠AFC为二面角AMNC的平面角，
∵AF＝CF＝eq \f(\r(6),2)，AC＝eq \r(2)，
∴AF2＋CF2≠AC2，即∠AFC≠eq \f(π,2)，
∴平面CMN与平面AMN不垂直，故C错误；
∵DE∥AN，MN∥BD，DE∩BD＝D，DE⊂平面BDE，BD⊂平面BDE，MN∩AN＝N，MN⊂平面AMN，AN⊂平面AMN，
∴平面BDE∥平面AMN，故D正确．故选ABD.
10．将边长为的正方形沿对角线折起得到三棱锥，且，则下列结论正确的是（）
A．
B．平面平面
C．三棱锥的外接球的体积为
D．三棱锥的表面积为
【答案】ABD
【解析】
对于A，取的中点，连接，，则，，
所以平面，所以．所以A正确；
对于B，由，，得是二面角的平面角，
由，易得，
所以，从而，故，
所以平面平面，所以B正确；
对于C，易知，
所以，所以为三棱锥的外接球球心，
且外接球半径为，所以三棱锥外接球的体积为，所以C错误；
对于D，易知和是全等的直角三角形，和是全等的正三角形，所以三棱表面积，所以D正确．故选ABD.
三、填空题
11．(2020·全国Ⅱ改编)设有下列四个命题：
①两两相交且不过同一点的三条直线必在同一平面内；
②过空间中任意三点有且仅有一个平面；
③若空间两条直线不相交，则这两条直线平行；
④若直线l⊂平面α，直线m⊥平面α，则m⊥l.
则上述命题中所有真命题的序号是________．
【答案】①④
【解析】①是真命题，两两相交且不过同一点的三条直线必定有三个交点，且这三个交点不在同一条直线上，由平面的基本性质“经过不在同一直线上的三个点，有且只有一个平面”，可知①为真命题；②是假命题，因为空间三点在一条直线上时，有无数个平面过这三个点；③是假命题，因为空间两条直线不相交时，它们可能平行，也可能异面；④是真命题，因为一条直线垂直于一个平面，那么它垂直于平面内的所有直线．从而①④为真命题．
12．(2020·广州市调研检测)已知正方体ABCDA1B1C1D1的棱长为2，M为CC1的中点．若AM⊥平面α，且B∈平面α，则平面α截正方体所得截面的周长为________．
【答案】3eq \r(2)＋2eq \r(5)
【解析】如图，连接AC，BD，在正方体ABCDA1B1C1D1中，BD⊥AC，又BD⊥CC1，AC∩CC1＝C，所以BD⊥平面AMC，故BD⊥AM，取BB1的中点N，A1B1的中点E，连接MN，AN，BE，可知BE⊥AN，因为MN⊥平面ABB1A1，所以MN⊥BE，又AN∩MN＝N，所以BE⊥平面AMN，故BE⊥AM，结合BD⊥AM，BD∩BE＝B，可知AM⊥平面DBE，取A1D1的中点F，连接DF，EF，则截面即四边形BEFD，因为DF＝EB＝eq \r(22＋12)＝eq \r(5)，BD＝eq \r(22＋22)＝2eq \r(2)，EF＝eq \r(2)，所以截面BEFD的周长为3eq \r(2)＋2eq \r(5).
13．(2020·东北三校联考)如图，四边形ABCD是边长为2的正方形，ED⊥平面ABCD，FC⊥平面ABCD，ED＝2FC＝2，则异面直线AE与BF所成角的余弦值为________．
【答案】eq \f(3\r(10),10)
【解析】因为ED⊥平面ABCD，FC⊥平面ABCD，所以ED∥FC.取ED的中点为G，连接AG，FG，如图，因为ED＝2FC，所以DG＝FC，且DG∥FC，所以四边形CDGF为平行四边形，则FG∥CD且FG＝CD.又四边形ABCD为正方形，所以CD∥AB，CD＝AB，则FG∥AB且FG＝AB，则四边形ABFG为平行四边形，则BF∥AG，则∠EAG是AE与BF所成的角．由正方形ABCD的边长为2，ED＝2FC＝2，可得AE＝2eq \r(2)，AG＝eq \r(5)，EG＝1，在△AEG中，由余弦定理得cs∠EAG＝eq \f(AG2＋AE2－EG2,2AE·AG)＝eq \f(5＋8－1,2×2\r(2)×\r(5))＝eq \f(3\r(10),10).
14．（2021·湖北武汉市高三三模）如图，在边长为的正方形中，、分别是、的中点.若沿、及把这个正方形折成一个四面体，使、、三点重合，重合后的点记为，则：
（1）三棱锥外接球的表面积为___________；
（2）点到平面的距离为___________.
【答案】
【解析】（1）在正方形中，，，，
在三棱锥中，则，，
，平面，且，
将三棱锥补成长方体，
所以三棱锥外接球的直径为，
因此，三棱锥外接球的表面积为；
（2），，
，取的中点，连接，则，
，则，
设点到平面的距离为，由，可得，解得.
四、解答题
15．（2021•全国高考甲卷文科）已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，.
（1）求三棱锥的体积；
（2）已知D为棱上的点，证明：.
【解析】(1) 解：如图所示，连结AF.
由题意可得，
由于AB⊥BB1，BC⊥AB，，故平面，
而平面，故，
从而有，
从而，
则，为等腰直角三角形，
，.
证明：由(1)结论可将几何体补形为一个棱长为2的正方体，如图所示，取棱的中点，连结，
正方形中，为中点，则，
又，
故平面，而平面，
从而.
16．（2021·黑龙江哈九中高三三模（文））如图，已知三棱柱的底面是正三角形，侧面是矩形，、分别为、的中点，为上一点．过和的平面交于，交于．
（1）证明：，且平面平面；
（2）设为的中心．若，平面，且，求四棱锥的体积．
【解析】（1）证明：在三棱柱中，且，故四边形为平行四边形，
所以，且，
因为、分别为、的中点，则且，
故四边形为平行四边形，所以，，
又因为，因此，.
，为的中点，则，
平面，平面，故，
，则，
，平面，
平面，平面，平面平面，则，
，，所以，平面，
因为平面，因此，平面平面；
（2）解：平面，平面，平面平面，
故，
又因为，故四边形为平行四边形，所以，，
为的中心，则，
，，则四边形为平行四边形，
所以，，，，
因为且，则四边形为平行四边形，故，
平面，平面，故平面，
所以点到平面的距离等于点到平面的距离，
过点在平面内作，垂足为点，
因为平面平面，平面平面，平面，，故平面，
所以，，
，
所以，.