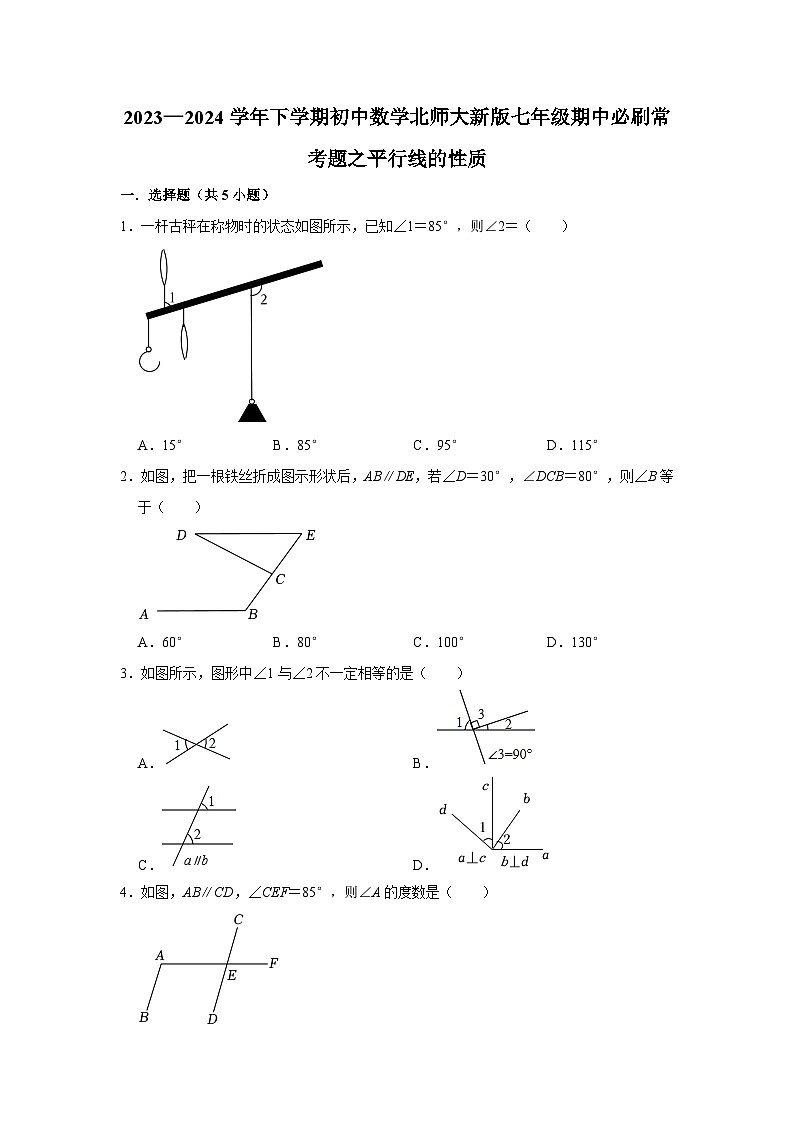

2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之平行线的性质
展开A.15°B.85°C.95°D.115°
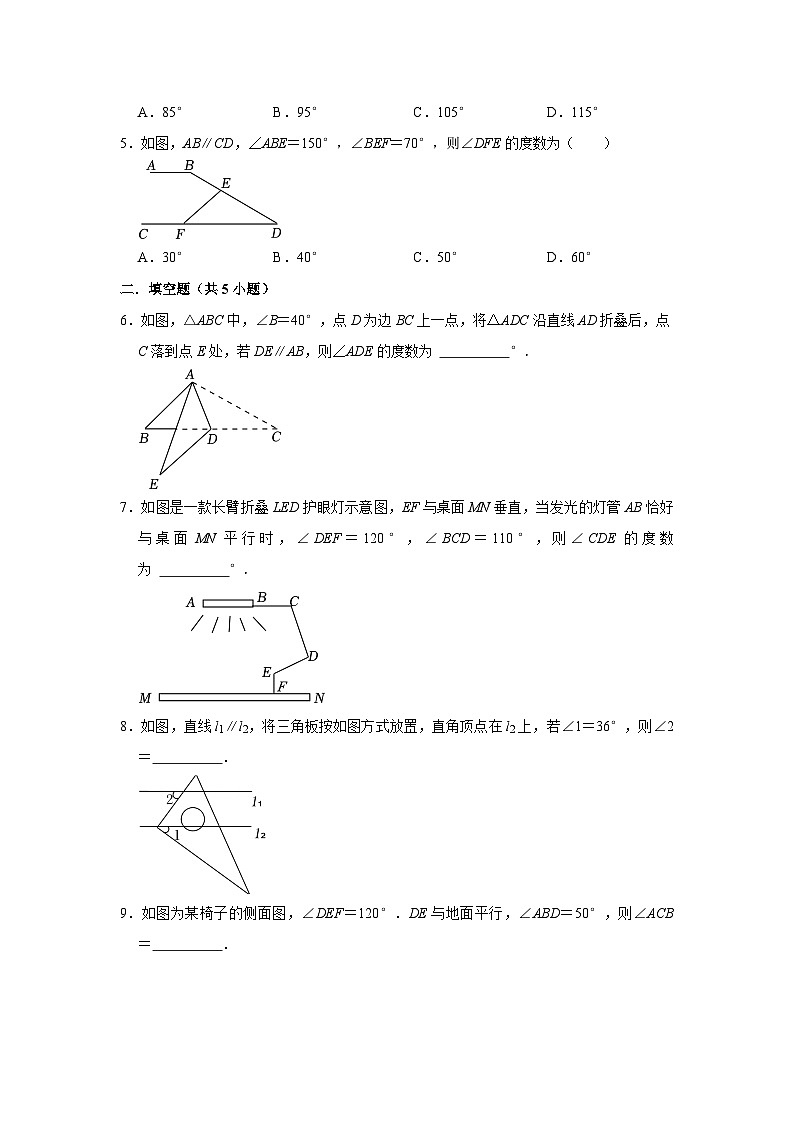
2.如图,把一根铁丝折成图示形状后,AB∥DE,若∠D=30°,∠DCB=80°,则∠B等于( )
A.60°B.80°C.100°D.130°
3.如图所示,图形中∠1与∠2不一定相等的是( )
A.B.
C.D.
4.如图,AB∥CD,∠CEF=85°,则∠A的度数是( )
A.85°B.95°C.105°D.115°
5.如图,AB∥CD,∠ABE=150°,∠BEF=70°,则∠DFE的度数为( )
A.30°B.40°C.50°D.60°
二.填空题(共5小题)
6.如图,△ABC中,∠B=40°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为 °.
7.如图是一款长臂折叠LED护眼灯示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=120°,∠BCD=110°,则∠CDE的度数为 °.
8.如图,直线l1∥l2,将三角板按如图方式放置,直角顶点在l2上,若∠1=36°,则∠2= .
9.如图为某椅子的侧面图,∠DEF=120°.DE与地面平行,∠ABD=50°,则∠ACB= .
10.如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= °.
三.解答题(共5小题)
11.已知:直线AB∥CD,点P在AB的上方,且∠AEP=50°,∠PFC=120°.
(1)如图1,求∠EPF的度数;
(2)如图2,若∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.
12.【问题情境】:在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D.
【探索发现】:
(1)当∠A=60°时,求证:∠CBD=∠A;
(2)“快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系.
①当∠A=40°时,∠CBD= 度;
②当∠A=x°时,∠CBD= 度(用含x的代数式表示);
【操作探究】:
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变.请写出它们的关系,并说明理由.
13.如图,AB∥CD,CE平分∠ACD,∠A=108°,求∠AEC的度数.
14.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= 度,∠FOH= 度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
15.如图,点D在线段AB上,点E、F在线段BC上,DE∥AC,DF∥AE,DF平分∠BDE.试说明:AE平分∠BAC.
解:因为DF平分∠BDE(已知),
所以 (角平分线定义).
因为DF∥AE(已知),
所以∠3=∠4(理由: ),
∠2=∠5(理由: ),
所以∠2=∠3=∠4=∠5(等式的性质).
因为DE∥AC(已知),
所以∠3= (两直线平行,内错角相等),
所以 (等式性质),
所以AE平分∠BAC(理由: ).
2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之平行线的性质
参考答案与试题解析
一.选择题(共5小题)
1.一杆古秤在称物时的状态如图所示,已知∠1=85°,则∠2=( )
A.15°B.85°C.95°D.115°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】C
【分析】根据两直线平行,内错角相等,和邻补角关系计算即可.
【解答】解:如图,根据生活意义,得到a,
∴∠3=∠1=85°;
∵∠3+∠2=180°,
∴∠3=95°.
故选:C.
【点评】本题考查了两直线平行,内错角相等,和邻补角关系,熟练掌握平行线的性质是解题的关键.
2.如图,把一根铁丝折成图示形状后,AB∥DE,若∠D=30°,∠DCB=80°,则∠B等于( )
A.60°B.80°C.100°D.130°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】根据三角形外角的性质求出∠E,再由平行线的性质表示出即可得出答案.
【解答】解:∵∠D=30°,∠DCB=80°,
∴∠E=80°﹣30°=50°.
∵AB∥DE,
∴∠B=180°﹣∠E=130°.
故选:D.
【点评】本题考查了平行线的性质,三角形外角的性质.熟练掌握各知识点是解题的关键.
3.如图所示,图形中∠1与∠2不一定相等的是( )
A.B.
C.D.
【考点】平行线的性质;余角和补角;对顶角、邻补角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】B
【分析】根据对顶角相等,平行线的性质,余角和补角的意义,逐一判断即可解答.
【解答】解:A、∵∠1与∠2是对顶角,
∴∠1=∠2,
故A不符号题意;
B、∵∠3=90°,
∴∠1+∠2=180°﹣∠3=90°,
∴∠1与∠2不一定相等,
故B符合题意;
C、∵a∥b,
∴∠1=∠2,
故C不符合题意;
D、如图:
∵a⊥c,b⊥d,
∴∠ABC=∠DBF=90°,
∴∠DBF﹣∠ABF=∠ABC﹣∠ABF,
∴∠1=∠2,
故D不符合题意;
故选:B.
【点评】本题考查了平行线的性质,余角和补角,对顶角和邻补角,熟练掌握这些数学概念是解题的关键.
4.如图,AB∥CD,∠CEF=85°,则∠A的度数是( )
A.85°B.95°C.105°D.115°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】先根据邻补角互补求出∠DEF的度数,再根据两直线平行,同位角相等得出∠A=∠DEF,即可求出∠A的度数.
【解答】解:∵∠CEF=85°,
∴∠DEF=180°﹣∠CEF=180°﹣85°=95°,
∵AB∥CD,
∴∠A=∠DEF=95°,
故选:B.
【点评】本题考查了平行线的性质,邻补角的性质,熟练掌握这两个性质是解题的关键.
5.如图,AB∥CD,∠ABE=150°,∠BEF=70°,则∠DFE的度数为( )
A.30°B.40°C.50°D.60°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】分别过点E作EG∥AB,再根据平行线的性质即可得出结论.
【解答】解:过E作EG∥AB,如图所示:
∵AB∥CD,
∴EG∥CD,
∴∠ABE+∠BEG=180°,
∴∠BEG=30°,
∵∠BEF=70°,
∴∠GEF=70°﹣30°=40°,
∵AB∥CD∥EG,
∴∠DFE=∠GEF=40°,
故选:B.
【点评】本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
二.填空题(共5小题)
6.如图,△ABC中,∠B=40°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为 110 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;运算能力.
【答案】110.
【分析】根据平行线的性质得到∠BDE=∠B=40°,根据折叠的性质得到∠ADE=∠ADC,根据平角的定义可得∠ADB+∠ADC=180°,由此可以求出∠ADC的度数即可得到答案.
【解答】解:∵DE∥AB,∠B=40°,
∴∠BDE=40°,
由折叠的性质得∠ADE=∠ADC,
∵∠ADB+∠ADC=180°,∠ADB=∠ADE﹣∠BDE=∠ADC﹣40°,
∴∠ADC﹣40°+∠ADC=180°,
∴∠ADC=110°,
∴∠ADE=∠ADC=110°.
故答案为:110.
【点评】本题考查了折叠的性质,平行线的性质,熟练掌握平行线的性质、折叠的性质是解题的关键.
7.如图是一款长臂折叠LED护眼灯示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=120°,∠BCD=110°,则∠CDE的度数为 100 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】100°.
【分析】过点D作DG∥AB,过点E作EH∥AB,根据平行线的性质求解即可;
【解答】解:∵EF⊥MN,
∴∠MFE=90°,
如图,过点D作DG∥AB,过点E作EH∥AB,
∵AB∥MN,
∴AB∥DG∥EH∥MN,
∴∠ACD+∠CDG=180°,∠GDE=∠DEF,∠HEF=∠MFE=90°,∠DEH=GDE,
∵∠DEF=120°,∠BCD=110°,
∴∠GDE=∠DEH=30°,∠CDG=180°﹣110°=70°,
∴∠CDE=∠CDG+∠GDE=100°,
故答案为:100°.
【点评】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
8.如图,直线l1∥l2,将三角板按如图方式放置,直角顶点在l2上,若∠1=36°,则∠2= 54° .
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】54°.
【分析】由题意可得∠BAC=90°,从而可求得∠BAD的度数,再由平行线的性质即可求∠2的度数.
【解答】解:如图,
由题意得:∠BAC=90°,
∵∠1=36°,
∴∠BAD=∠BAC﹣∠1=54°,
∵l1∥l2,
∴∠2=∠BAD=54°.
故答案为:54°.
【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.
9.如图为某椅子的侧面图,∠DEF=120°.DE与地面平行,∠ABD=50°,则∠ACB= 70° .
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】70°.
【分析】根据平行得到∠ABD=∠EDC=50°,再利用外角的性质和对顶角相等,进行求解即可.
【解答】解:由题意得:DE∥AB,
∴∠ABD=∠EDC=50°,
∵∠DEF=∠EDC+∠DCE=120°,
∴∠DCE=70°,
∴∠ACB=∠DCE=70°,
故答案为:70°.
【点评】本题考查平行线的性质,三角形外角的性质,对顶角.熟练掌握相关性质,是解题的关键.
10.如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= 72 °.
【考点】平行线的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;几何直观;推理能力.
【答案】72.
【分析】先根据∠DEF=72°求出∠EFC的度数,进可得出∠EFB和∠BFH的度数,根据∠H=90°和三角形的内角和可得∠HMF的度数,再由折叠的性质可得∠GMN.
【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
【点评】本题考查的是平行线的性质,由折叠的性质得到角相等是解题关键.
三.解答题(共5小题)
11.已知:直线AB∥CD,点P在AB的上方,且∠AEP=50°,∠PFC=120°.
(1)如图1,求∠EPF的度数;
(2)如图2,若∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)70°;
(2)35°.
【分析】(1)过点P作PM∥AB,根据平行线的判定和性质解答即可;
(2)过点G作GM∥AB,根据平行线的判定和性质解答即可.
【解答】解:(1)如图1,过点P作PM∥AB,
∴∠MPE=∠AEP=50°,
∵AB∥CD,
∴PM∥CD,
∴∠PFC=∠MPF=120°,
∴∠EPF=∠MPF﹣∠MPE=120°﹣50°=70°;
(2)如图2所示,
∵EG是∠PEA的平分线,FG是∠PFC的平分线,
∴,,
过点G作GM∥AB,
∴∠MGE=∠AEG=25°,
∵AB∥CD,
∴GM∥CD,
∴∠GFC=∠MGF=60°,
∴∠EGF=∠MGF﹣∠MGE=60°﹣25°=35°.
【点评】此题考查平行线的性质,关键是根据两直线平行,内错角相等解答.
12.【问题情境】:在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D.
【探索发现】:
(1)当∠A=60°时,求证:∠CBD=∠A;
(2)“快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系.
①当∠A=40°时,∠CBD= 70 度;
②当∠A=x°时,∠CBD= (90x). 度(用含x的代数式表示);
【操作探究】:
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变.请写出它们的关系,并说明理由.
【考点】平行线的性质;列代数式.
【专题】线段、角、相交线与平行线;几何直观;运算能力;推理能力.
【答案】(1)答案见解答过程;
(2)①70°;②(90x);
(3)∠APB=2∠ADB,理由见解答过程.
【分析】(1)由AM∥BN,∠A=60可得∠ABN=120°,再根据角平分线的定义得∠PBD∠PBN,∠CBP∠ABP,由此可得∠CBD=∠PBD+∠CBP(∠PBN+∠ABP)∠ABN=60°,据此可得出结论;
(2)由AM∥BN得∠ABN=180°﹣∠A,进而可得∠CBD∠ABN=90°∠A;①将∠A=40°代入∠CBD=90°∠A即可得出答案;②当∠A=x°代入∠CBD=90°∠A即可得出答案;
(3)由AM∥BN,∠APB=∠PBN,∠ADB=∠NBD,再根据角平分线的定义得BD平分∠PBN得∠PBN=2∠NBD,由此可得∠APB与∠ADB之间的数量关系.
【解答】(1)证明:∵AM∥BN,∠A=60°,
∴∠ABN=180°﹣∠A=120°,
∵BC,BD分别平分∠ABP和∠PBN,
∴∠PBD∠PBN,∠CBP∠ABP,
∴∠PBD+∠CBP(∠PBN+∠ABP)∠ABN,
∴∠CBD=∠PBD+∠CBP∠ABN=60°,
∴∠CBD=∠A;
(2)∠CBD与∠A存在的数量关系是:∠CBD=90°∠A,理由如下:
∵AM∥BN,
∴∠ABN=180°﹣∠A,
由(1)可知:∠CBD∠ABN,
∴∠CBD=1/2(180°﹣∠A)=90°∠A.
①当∠A=40°时,
∴∠CBD=90°40°=70°,
故答案为:70.
②当∠A=x°时,
∴∠CBD=90°∠A=90°x°.
故答案为:(90x).
(3)∠APB与∠ADB之间的数量关系是:∠APB=2∠ADB,理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠NBD,
∵BD平分∠PBN,
∴∠PBN=2∠NBD,
∴∠APB=2∠NBD.
【点评】此题主要考查了平行线的性质,角平分线的定义,理解题意,准确识图,熟练掌握平行线的性质,角平分线的定义是解决问题的关键.
13.如图,AB∥CD,CE平分∠ACD,∠A=108°,求∠AEC的度数.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】36°.
【分析】先由AB∥CD,∠A=108°,得∠ACD的度数,再根据CE平分∠ACD,可得∠DCE的度数,再根据两直线平行,内错角相等求出结论.
【解答】解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=108°,
∴∠ACD=180°﹣∠A=180°﹣108°=72°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=36°,
∵AB∥CD,
∴∠AEC=∠DCE=36°.
【点评】本题考查了平行线的性质,熟记性质并灵活运用是解题的关键,两直线平行,同位角相等,同旁内角互补,内错角相等.
14.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= 30 度,∠FOH= 125 度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
【考点】平行线的性质;列代数式.
【专题】线段、角、相交线与平行线.
【答案】见试题解答内容
【分析】【探究】(1)依据角平分线以及平行线的性质,即可得到∠EOF的度数,依据三角形内角和定理,即可得到∠FOH的度数;
(2)依据角平分线以及平行线的性质、三角形内角和定理,即可得到∠FOH的度数;
【拓展】根据∠AFH和∠CHI的平分线交于点O,可得∠OFH∠AFH,∠OHI∠CHI,再根据∠FOH=∠OHI﹣∠OFH进行计算,即可得到∠FOH的度数.
【解答】解:【探究】(1)∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°﹣∠OFH﹣∠OHF=125°;
故答案为:30,125;
(2)∵FO平分∠AFH,HO平分∠CHF,
∴∠OFH∠AFH,∠OHF∠CHF.
∵∠AFH+∠CHF=100°,
∴∠OFH+∠OHF(∠AFH+∠CHF)100°=50°.
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
∴∠FOH=180°﹣(∠EOF+∠GOH )=180°﹣50°=130°.
【拓展】∵∠AFH和∠CHI的平分线交于点O,
∴∠OFH∠AFH,∠OHI∠CHI,
∴∠FOH=∠OHI﹣∠OFH
(∠CHI﹣∠AFH)
(180°﹣∠CHF﹣∠AFH)
(180°﹣α)
=90°α.
【点评】本题主要考查了平行线的性质以及三角形内角和定理的综合运用,解决问题的关键是掌握:两直线平行,内错角相等.
15.如图,点D在线段AB上,点E、F在线段BC上,DE∥AC,DF∥AE,DF平分∠BDE.试说明:AE平分∠BAC.
解:因为DF平分∠BDE(已知),
所以 ∠4=∠5 (角平分线定义).
因为DF∥AE(已知),
所以∠3=∠4(理由: 两直线平行,内错角相等 ),
∠2=∠5(理由: 两直线平行,同位角相等 ),
所以∠2=∠3=∠4=∠5(等式的性质).
因为DE∥AC(已知),
所以∠3= ∠1 (两直线平行,内错角相等),
所以 ∠1=∠2 (等式性质),
所以AE平分∠BAC(理由: 角平分线定义 ).
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】∠4=∠5;两直线平行,内错角相等;两直线平行,同位角相等;∠1;∠1=∠2;角平分线定义.
【分析】由角平分线的定义可得∠4=∠5,再由平行线的性质可得∠3=∠4,∠2=∠5,则有∠2=∠3=∠4=∠5,即可判定DE∥AC,则有∠3=∠1,可得∠1=∠2,即可判定AE平分∠BAC.
【解答】解:因为DF平分∠BDE(已知),
所以∠4=∠5(角平分线定义).
因为DF∥AE(已知),
所以∠3=∠4(理由:两直线平行,内错角相等),
∠2=∠5(理由:两直线平行,同位角相等),
所以∠2=∠3=∠4=∠5(等式的性质).
因为DE∥AC(已知),
所以∠3=∠1(两直线平行,内错角相等),
所以∠1=∠2(等式性质),
所以AE平分∠BAC(理由:角平分线定义).
故答案为:∠4=∠5;两直线平行,内错角相等;两直线平行,同位角相等;∠1;∠1=∠2;角平分线定义.
【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.
考点卡片
1.列代数式
(1)定义:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
(2)列代数式五点注意:①仔细辨别词义. 列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分. ②分清数量关系.要正确列代数式,只有分清数量之间的关系. ③注意运算顺序.列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.④规范书写格式.列代数时要按要求规范地书写.像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号.注意代数式括号的适当运用. ⑤正确进行代换.列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换.
【规律方法】列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“•”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
2.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
3.对顶角、邻补角
(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
(3)对顶角的性质:对顶角相等.
(4)邻补角的性质:邻补角互补,即和为180°.
(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.
4.平行线的性质
1、平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
定理2:两条平行线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
2、两条平行线之间的距离处处相等.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/2/29 16:24:17;用户:组卷4;邮箱:zyb004@xyh.cm;学号:41418967
菁优网APP 菁优网公众号 菁优网小程序
2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的除法: 这是一份2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的除法,共15页。试卷主要包含了下列运算正确的是,计算等内容,欢迎下载使用。
2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的乘法: 这是一份2023—2024学年下学期初中数学北师大新版七年级期中必刷常考题之整式的乘法,共15页。试卷主要包含了已知,计算等内容,欢迎下载使用。
2023—2024学年下学期初中数学北师大新版九年级期中必刷常考题之切线长定理: 这是一份2023—2024学年下学期初中数学北师大新版九年级期中必刷常考题之切线长定理,共22页。












