河南省安阳市滑县实验学校2022-2023学年八年级下学期期中数学试卷(含答案)

这是一份河南省安阳市滑县实验学校2022-2023学年八年级下学期期中数学试卷(含答案)，共19页。试卷主要包含了单选题，解答题，填空题等内容，欢迎下载使用。


一、单选题
1．以下列各组数为边长，能组成直角三角形的是( )
A.1，2，3B.1，，2C.2，，D.7，12，13
2．下列各条件中，能判定一个四边形是平行四边形的是( )
A.对角线互相平分B.一组对角相等C.对角线相等D.一组邻边相等
3．下列计算正确的是( )
A.B.C.D.
4．如图，小乐为测量自家池塘边上两点间的距离，在池塘的一侧选取一点，记的中点分别为点，测得米，则间的距离是( )
A.18米B.24米C.34米D.36米
5．要使有意义，x的取值可以是( )
A.2B.3C.4D.5
6．如图，一棵大树被台风刮断，若树在离地面处折断，树顶端落在离树底部处，则树折断之前高( )
A.B.C.D.
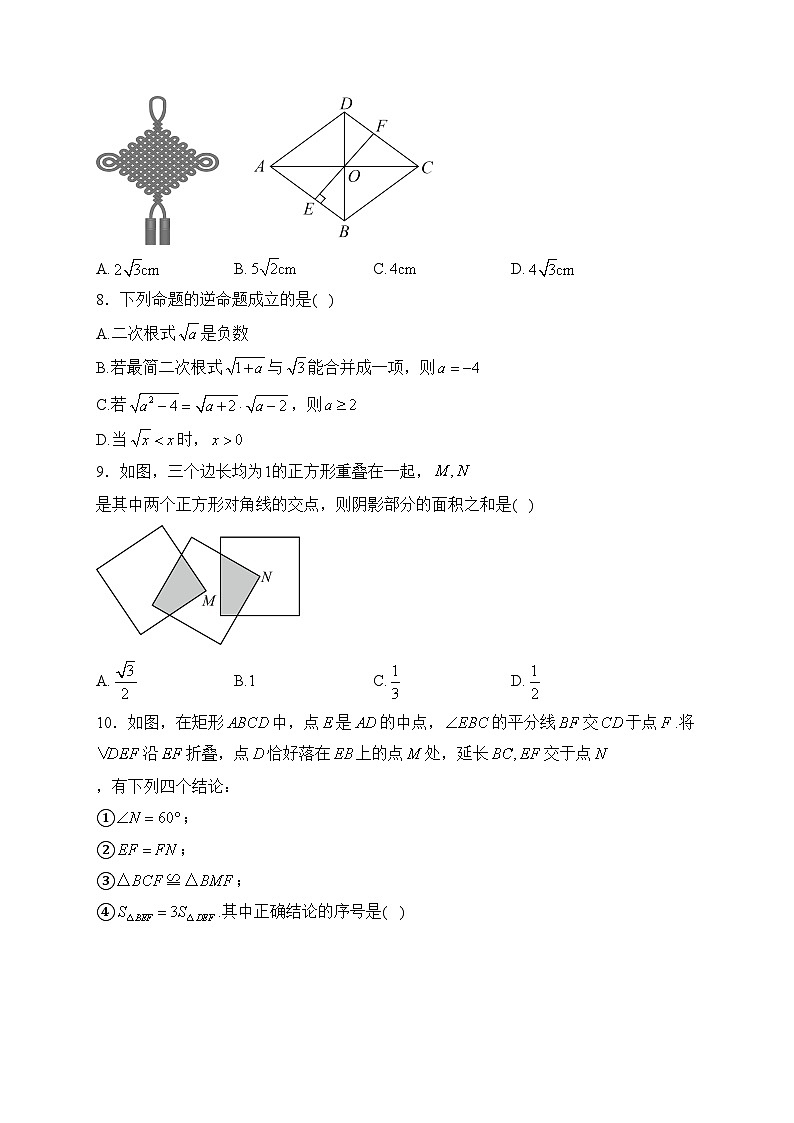
7．中国结象征着中华民族的历史文化与精神.小乐家有一中国结挂饰，他想求两对边的距离，于是利用所学知识抽象出如图所示的菱形，测得，直线过点且与垂直，分别交于，则的长为( )
A.B.C.D.
8．下列命题的逆命题成立的是( )
A.二次根式是负数
B.若最简二次根式与能合并成一项，则
C.若，则
D.当时，
9．如图，三个边长均为1的正方形重叠在一起，是其中两个正方形对角线的交点，则阴影部分的面积之和是( )

A.B.1C.D.
10．如图，在矩形中，点是的中点，的平分线交于点.将沿折叠，点恰好落在上的点处，延长交于点，有下列四个结论：
①；
②；
③；
④.其中正确结论的序号是( )
A.①②③B.①③④C.②③④D.①②③④⑤
二、解答题
11．如图，要使平行四边形成为矩形，可以添加的条件是_____.
12．如图，在平面直角坐标系中，的顶点B在x轴上，点A的坐标为，以点O为圆心，任意长为半径画弧，分别交于点D，E，再分别以点D，E为圆心，以大于的长为半径作弧，两弧在内交于点F，作射线交于点P.则点P的坐标是_____.

13．如图，直线上有三个正方形，若的面积分别为2和4，则的边长为_____.

14．如图，在Rt中，为边上一点，，垂足分别是，连接，则的最小值为_____.

15．计算：
(1)；
(2).
16．如图，在中，点，在对角线上，连接，，使得，求证：，.
17．在第十四届全国人大一次会议召开之际，某中学举行了庄严的升旗仪式.看着着冉升起的五星红旗（如图1），小乐想用刚学过的知识计算旗杆的高度.如图2，为旗杆上用来固定国旗的绳子，点距地面的高度.将绳子拉至的位置，测得点到的距离，到地面的垂直高度，求旗杆的高度.
18．如图，已知，延长到，使，连接交于点，连接.若，
(1)求证：四边形是矩形；
(2)若，求的度数.
19．如图，正方形网格中有.若每个小方格的边长都为1，请你根据所学的知识解答下列问题：
(1)求的周长；
(2)判断的形状，并说明理由.
20．在解决问题“已知，求的值”时，小明是这样分析与解答的：
，
，
请你根据小明的分析过程，解决如下问题：
(1)化简：；
(2)若，求的值.
21．小明在学习菱形时，对矩形进行了画图探究，其作法和图形如下：
①连接；
②分别以点为圆心，大于的长为半径作弧，两弧相交于两点，作直线交于点，交于点；
③连接.
(1)根据以上作法，判断四边形的形状，并说明理由；
(2)若，求四边形的周长.
22．如图1，在正方形中，是边上一点（点不与点重合），点是的中点，.
(1)如图2，过点作交于点，交于点.
①求证：；
②求的长.
(2)如图3，过点作交于点，连接.直接写出四边形的面积.
三、填空题
23．若是整数，则正整数的最小值是_____.
参考答案
1．答案：B
解析：A、∵，∴A不能组成直角三角形，不符合题意；
B、∵，∴B能组成直角三角形，符合题意；
C、，∴C不能组成直角三角形，不符合题意；
D、∵，∴D不能 直角三角形，不符合题意；
故选：B.
2．答案：A
解析：、对角线互相平分的四边形是平行四边形，本选项正确，符合题意；
、两组对角分别相等的四边形是平行四边，故本选项错误，不符合题意；
、等腰梯形的对角线也相等，不是平行四边形，故本选项错误，不符合题意；
、如图，，一组邻边相等却不是平行四边形，故本选项错误，不符合题意.
3．答案：B
解析：A.不是同类项，不可以合并，不符合题意；
B.，计算正确，符合题意；
C.，选项计算错误，不符合题意；
D.，选项计算错误，不符合题意；
故选：B.
4．答案：D
解析：连接，
∵的中点分别为点，
∴是的中位线，
∵米，
∴米，
故选：D.
5．答案：A
解析：∵2-x≥0，
∴x≤2，
∴x可以是2，
故选：A.
6．答案：D
解析：如图；.
在中，米，，
由勾股定理，得：，
，即大树折断之前有高.
故选：D.
7．答案：A
解析：∵四边形是菱形，
∴，，，
∵，
∴是等边三角形，
∴，
根据勾股定理可得：，
∴，
∵，
∴，
解得：，
故选：A.
8．答案：C
解析：A、“二次根式是负数”的逆命题是“如果是负数，那么是二次根式”是假命题，不符合题意；
B、“若最简二次根式与能合并成一项，则”的逆命题为：“若，则最简二次根式与能合并成一项”，是假命题，不符合题意；
C、“若，则”的逆命题为“若，则”，是真命题，符合题意；
D、“当时，”的逆命题为“当时，则”，是假命题，不符合题意；
故选：C.
9．答案：D
解析：连接，，如图所示：
三个边长均为1的正方形重叠在一起，、是其中两个正方形对角线的交点，
，，
，
四边形是正方形，
，，
在和中
，
两个正方形阴影部分的面积，
同理另外两个正方形阴影部分的面积也是，
.
故选：D.
10．答案：C
解析：∵四边形为矩形，
∴，
∵由沿折叠所得，
∴，，，
∵平分，，，
∴，
∴，
∵，
∴，
∴，故②正确，符合题意；
在和中，
，
∴，故③正确，符合题意；
∴，
∵点是的中点，
∴，
∴，
∴，
∵，，
∴，故④正确，符合题意；
连接，
∵，，
∴，即，
∵，点是的中点，
∴，
∵，
∴，
∴，
∵，
∴，即，
∴不是直角三角形，则，故①不正确，不符合题意；

综上：正确的有②③④，
故选：C.
11．答案：（答案不唯一）
解析：∵四边形是平行四边形，
∴当时，四边形是矩形，
故答案为：（答案不唯一）.
12．答案：
解析：∵点A坐标为，
∴
∵，

由作图可得：平分



故答案为：
13．答案：
解析：如图，
∵均为正方形，
∴，
∴，
∴，
在和中，
，
∴，
∴，
根据勾股定理可得：，
∴的边长为.
故答案为：.
14．答案：
解析：连接，如图：
，，
，
，
四边形是矩形，
，
要使最小，只要最小即可，
当时，最短，
，，，
，
的面积，
，
的最小值为，
故答案为：.
15．答案：(1)
(2)
解析：（1）
；
（2）
.
16．答案：证明见解析
解析：证明：∵四边形是平行四边形，
∴，，
∴，
在和中，
，
∴，
∴，，
∵，，
∴，
∴.
17．答案：
解析：∵，
∴，
∵，
∴，
设，则，，
由题意可得：，
在中，，
即，
解得：，即，
∴旗杆的高度为：.
18．答案：(1)见解析
(2)
解析：（1）在中，，，，，
∵，
∴，又，
∴四边形是平行四边形，
∵，
∴，又，
∴，
∴四边形是矩形；
（2）∵，
∴，
∴，
又，
∴，
∴是等边三角形，
∴，
∵，
∴.
19．答案：(1)
(2)直角三角形，理由见解析
解析：（1），
，
，
∴的周长为：；
（2）直角三角形，理由：
∵，，，
∴，
∴是直角三角形.
20．答案：(1)
(2)23
解析：（1）；
（2）∵，
∴，
∴，则，
∴，
∴.
21．答案：(1)见解析
(2)52
解析：（1）根据作图可知，是的垂直平分线，
∴，
∵四边形是矩形，
∴，
∴，
∴，
∴，
∴四边形是平行四边形，
∵是的垂直平分线，
∴，
∴四边形是菱形；
（2）设，
∵，
∴，
根据勾股定理可得：，
∵，
∴，
解得：，
由（1）可得：四边形是菱形，
∴四边形周长.
22．答案：(1)①见解析
②4
(2)4
解析：（1）①过点G作于点H，
∵四边形为正方形，
∴，，
∵，
∴四边形是矩形，
∴，
∵，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴；
②∵，点是的中点，，
∴，
由①可得：；
（2）过点N作于点Q，
∵四边形为正方形，
∴，，
∵，
∴四边形是矩形，
∴，
∵，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴；
∵点是的中点，
∴，
令与相交于点O，
∴.
23．答案：4
解析：∵有意义，
∴，解得：，
∵m是正整数，
∴，
∴，
∵是整数，
∴，
解得：，
∴正整数的最小值是4，
故答案为：4.