2025届高考数学一轮复习专项练习课时规范练34平面的基本事实与推论平行直线与异面直线

这是一份2025届高考数学一轮复习专项练习课时规范练34平面的基本事实与推论平行直线与异面直线，共6页。试卷主要包含了下列说法中正确的是等内容，欢迎下载使用。

1.(多选)下列说法中正确的是( )
A.空间中三条直线交于一点,则这三条直线共面
B.平行四边形可以确定一个平面
C.若一个角的两边分别平行于另一个角的两边,则这两个角相等
D.若A∈α,A∈β,且α∩β=l,则A在l上
2.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是( )
3.已知空间中不过同一点的三条直线l,m,n.“l,m,n共面”是“l,m,n两两相交”的( )

A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
4. l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )
A.l1⊥l2,l2⊥l3⇒l1∥l3
B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒l1,l2,l3共面
D.l1,l2,l3共点⇒l1,l2,l3共面
5.设P1,P2,P3,P4为空间中的四个不同点,则“P1,P2,P3,P4中有三点在同一条直线上”是“P1,P2,P3,P4在同一个平面上”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.(多选)已知A,B,C表示不同的点,l表示直线,α,β表示不同的平面,则下列推理正确的是( )
A.A∈l,A∈α,B∈l,B∈α⇒l⊂α
B.l⊄α,A∈l⇒A∉α
C.A∈α,A∈l,l⊄α⇒l∩α=A
D.A∈α,A∈β,B∈α,B∈β⇒α∩β=AB
7.
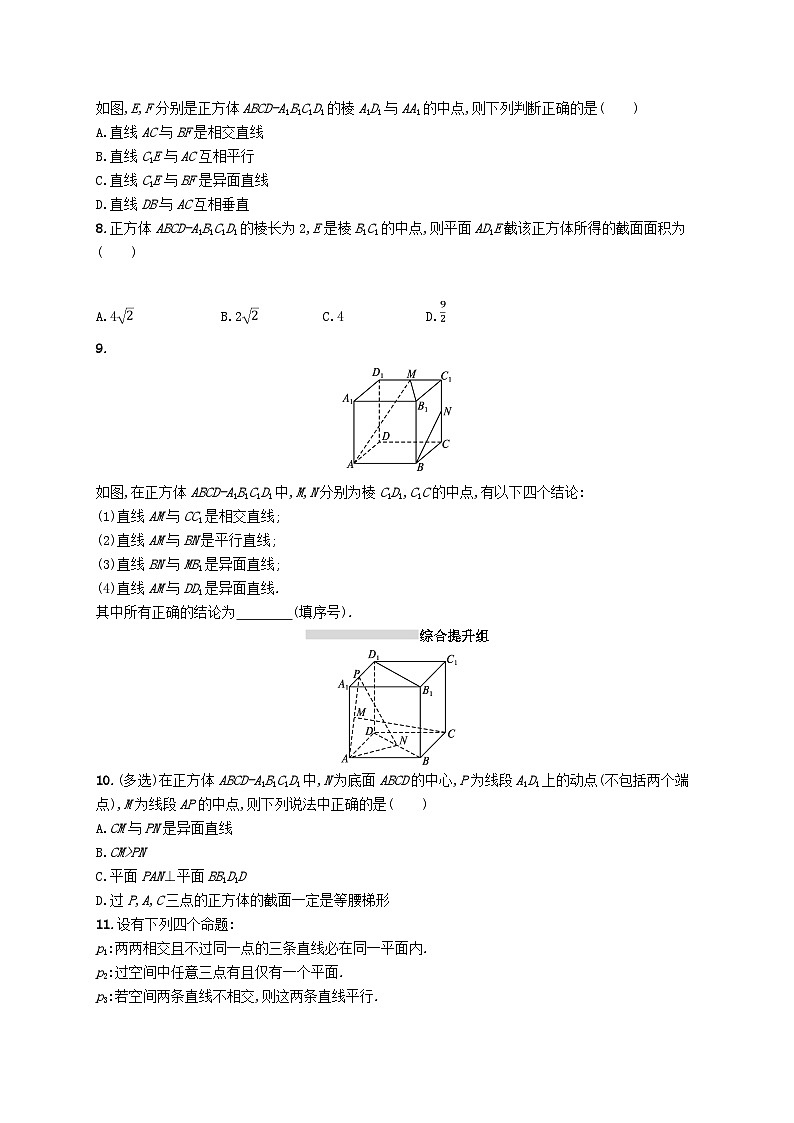
如图,E,F分别是正方体ABCD-A1B1C1D1的棱A1D1与AA1的中点,则下列判断正确的是( )
A.直线AC与BF是相交直线
B.直线C1E与AC互相平行
C.直线C1E与BF是异面直线
D.直线DB与AC互相垂直
8.正方体ABCD-A1B1C1D1的棱长为2,E是棱B1C1的中点,则平面AD1E截该正方体所得的截面面积为( )

A.4B.2C.4D.
9.
如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:
(1)直线AM与CC1是相交直线;
(2)直线AM与BN是平行直线;
(3)直线BN与MB1是异面直线;
(4)直线AM与DD1是异面直线.
其中所有正确的结论为 (填序号).
综合提升组
10.(多选)在正方体ABCD-A1B1C1D1中,N为底面ABCD的中心,P为线段A1D1上的动点(不包括两个端点),M为线段AP的中点,则下列说法中正确的是( )
A.CM与PN是异面直线
B.CM>PN
C.平面PAN⊥平面BB1D1D
D.过P,A,C三点的正方体的截面一定是等腰梯形
11.设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l⊂平面α,直线m⊥平面α,则m⊥l.
则上述命题中的真命题是 .
12.如图,在多面体ABCDE中,平面ACD⊥平面ABC,AC⊥BC,BC=2AC=4,DA=DC=3,F是BC的中点,EF⊥平面ABC,EF=2.
(1)证明:A,B,E,D四点共面;
(2)求三棱锥B-CDE的体积.
创新应用组
13.正方体ABCD-A1B1C1D1的棱长为1,点K在棱A1B1上运动,过A,C,K三点作正方体的截面,若K为棱A1B1的中点,则截面面积为 ,若截面把正方体分成体积之比为2∶1的两部分,则= .
参考答案
课时规范练34 平面的基本事
实与推论、平行直线与异面直线
1.BD 对于A,两两相交的三条直线,若相交于同一点,则不一定共面,故A不正确;
对于B,平行四边形两组对边分别平行,则平行四边形是平面图形,故B正确;
对于C,若一个角的两边分别平行于另一个角的两边,则这两个角相等或互补,故C不正确;
对于D,由基本事实3可得,若A∈α,A∈β,α∩β=l,则A∈l,故D正确.故选BD.
2.D A,B,C图中四点一定共面,D中四点不共面.
3.B 由条件可知,当m,n,l在同一平面内时,三条直线不一定两两相交,有可能两条直线平行;或三条直线平行;反过来,当空间中不过同一点的三条直线m,n,l两两相交时,如图,
三个不同的交点确定一个平面,则m,n,l在同一平面内,
所以“m,n,l”共面是“m,n,l两两相交”的必要不充分条件.
故选B.
4.B 对于A,通过常见的正方体,从同一个顶点出发的三条棱两两垂直,故A错误;对于B,因为l1⊥l2,所以l1,l2所成的角是90°,又因为l2∥l3,所以l1,l3所成的角是90°,所以l1⊥l3,故B正确;对于C,如三棱柱中的三条侧棱平行,但不共面,故C错误;对于D,如三棱锥的三条侧棱共点,但不共面,故D错误.故选B.
5.A 由推论1:经过一条直线和这条直线外一点,有且只有一个平面,可得P1,P2,P3,P4在同一平面,故充分条件成立;由推论3:经过两条平行直线,有且只有一个平面,可得,当P1∈l1,P2∈l1,P3∈l2,P4∈l2,l1∥l2时,P1,P2,P3,P4在同一个平面上,但P1,P2,P3,P4中无三点共线,故必要条件不成立.故选A.
6.ACD 由点A,B,C表示不同的点,l表示直线,α,β表示不同的平面,
对于A,由A∈l,A∈α,B∈l,B∈α,可得l⊂α,所以A正确;对于B,由l⊄α,A∈l,根据直线与平面的位置关系,则A∉α或A∈α,所以B不正确;对于C,由A∈α,A∈l,l⊄α,根据直线与平面的位置关系,则l∩α=A,所以C正确;对于D,由A∈α,A∈β,B∈α,B∈β,可得α∩β=AB,所以D正确.故选ACD.
7.D 由题知,AC⊂平面ABCD,BF与平面ABCD交于点B,B∉AC,所以直线AC与BF是异面直线,故A错误;
AC⊂平面ACC1A1,EC1与平面ACC1A1交于点C1,C1∉AC,所以直线C1E与AC是异面直线,故B错误;
根据正方体性质EF∥AD1∥BC1,所以E,F,B,C1四点共面,所以直线C1E与BF不是异面直线,故C错误;
正方体各个表面均为正方形,所以直线DB与AC互相垂直,故D正确.故选D.
8.
D 由题意可得,如图所示,因为E,F分别是B1C1,BB1的中点,所以BC1∥EF,在正方体中,AD1∥BC1,所以AD1∥EF,所以A,D1,E,F在同一平面内,所以平面AD1E截该正方体所得的截面为平面AD1EF.因为正方体ABCD-A1B1C1D1的棱长为2,所以EF=,AD1=2,等腰梯形的高为,所以四边形AD1EF的面积S=,故选D.
9.④③ 直线AM与CC1是异面直线,直线AM与BN也是异面直线,故①②错误.结论③④正确.
10.BCD 由题知,点C,N,A共线,即CN,PM交于点A,所以A,N,C,P,M共面,因此CM,PN共面,故A错误;
记∠PAC=θ,则PN2=AP2+AN2-2AP·ANcsθ=AP2+AC2-AP·ACcsθ,CM2=AC2+AM2-2AC·AMcsθ=AC2+AP2-AP·ACcsθ,又APCM2-PN2=(AC2-AP2)>0,CM2>PN2,即CM>PN,故B正确;
在正方体中,AN⊥BD,BB1⊥平面ABCD,则BB1⊥AN,BB1∩BD=B,可得AN⊥平面BB1D1D,AN⊂平面PAN,从而可得平面PAN⊥平面BB1D1D,故C正确;
过P,A,C三点的正方体的截面与C1D1相交于点Q,则AC∥PQ,且PQ11.p1,p4 对于命题p1,可设l1与l2相交,这两条直线确定的平面为α;
若l3与l1相交,则交点B在平面α内,
同理,l3与l2的交点A也在平面α内,
所以,AB⊂α,即l3⊂α,命题p1为真命题;
对于命题p2,若三点共线,则过这三个点的平面有无数个,命题p2为假命题;
对于命题p3,空间中两条直线的位置关系有相交、平行或异面,命题p3为假命题;
对于命题p4,若直线m⊥平面α,则m垂直于平面α内所有直线,
∵直线l⊂平面α,∴直线m⊥直线l,命题p4为真命题.
综上可知,p1,p4为真命题,p2,p3为假命题.
12.(1)证明 如图,取AC的中点M,连接DM,MF,因为DA=DC=3,AC=2,M为AC的中点,所以DM⊥AC,且DM=2,
因为平面ACD⊥平面ABC,交线为AC,DM⊂平面ACD,
所以DM⊥平面ABC,又EF⊥平面ABC,所以DM∥EF,且DM=EF=2,
所以四边形DEFM是平行四边形,从而DE∥MF.
在△ABC中,M,F分别是AC,BC的中点,所以MF∥AB,
所以DE∥AB,从而A,B,E,D四点共面.
(2)由(1)DM∥EF,DM⊄平面BCE,EF⊂平面BCE,所以DM∥平面BCE,
所以点D到平面BCE的距离等于点M到平面BCE的距离,
则三棱锥D-BCE与三棱锥M-BCE的体积相等.因为AC⊥BC,BC=2AC=4,M为AC的中点,所以△BCM的面积为S△BCM=CM·BC=2,
又EF⊥平面ABC,且EF=2,所以VB-CDE=VD-BCE=VM-BCE=VE-BCM=S△BCM·EF=
13 (1)取B1C1的中点M,连接KM,MC,
∵KM∥A1C1,而A1C1∥AC,
∴KM∥AC,
∴A,C,M,K四点共面,且AK=MC.∴四边形ACMK是等腰梯形,如图,
KM=,AC=,AK=,AH=,
∴KH=,
∴S四边形ACMK=
(2)设B1K=x,取B1C1上的点M,使B1K=B1M=x,连接KM,MC,
∵KM∥A1C1,A1C1∥AC,∴KM∥AC,∴A,C,M,K四点共面,,
x2+×1=,
即x2+x-1=0,∵x>0,∴解得x=
即B1K=,则A1K=1-,
故