第04讲 基本不等式及其应用（课件）-2024年高考数学一轮复习课件（新教材新高考）

这是一份第04讲 基本不等式及其应用（课件）-2024年高考数学一轮复习课件（新教材新高考），共37页。PPT课件主要包含了PARTONE等内容，欢迎下载使用。

1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。 3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。 4、重视错题。“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
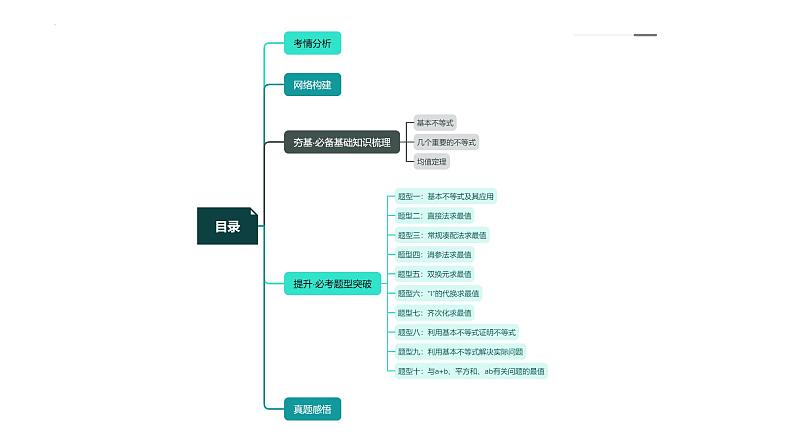
第04讲 基本不等式及其应用
知识梳理 题型归纳
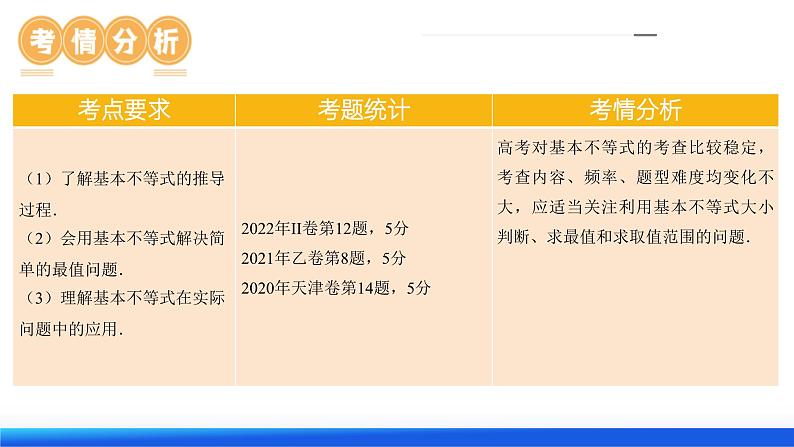
1.基本不等式：(1)基本不等式成立的条件： .(2)等号成立的条件：当且仅当 时，等号成立.(3)其中 叫做正数a，b的算术平均数， 叫做正数a，b的几何平均数.
2.几个重要的不等式(1)a2＋b2≥ (a，b∈R).(2) ≥ (a，b同号).(3)ab≤ (a，b∈R).(4) ≥ (a，b∈R).以上不等式等号成立的条件均为a＝b.
题型一：基本不等式及其应用
【解题方法总结】熟记基本不等式成立的条件，合理选择基本不等式的形式解题，要注意对不等式等号是否成立进行验证．
【解题方法总结】直接利用基本不等式求解，注意取等条件．
题型三：常规凑配法求最值
【解题方法总结】1、通过添项、拆项、变系数等方法凑成和为定值或积为定值的形式．2、注意验证取得条件．
【解题方法总结】消参法就是对应不等式中的两元问题，用一个参数表示另一个参数，再利用基本不等式进行求解．解题过程中要注意“一正，二定，三相等”这三个条件缺一不可！
【解题方法总结】若题目中含是求两个分式的最值问题，对于这类问题最常用的方法就是双换元，分布运用两个分式的分母为两个参数，转化为这两个参数的不等关系．1、代换变量，统一变量再处理．2、注意验证取得条件．
题型六：“1”的代换求最值
【解题方法总结】1的代换就是指凑出1，使不等式通过变形出来后达到运用基本不等式的条件，即积为定值，凑的过程中要特别注意等价变形．1、根据条件，凑出“1”，利用乘“1”法．2、注意验证取得条件．
【解题方法总结】齐次化就是含有多元的问题，通过分子、分母同时除以得到一个整体，然后转化为运用基本不等式进行求解．
题型八：利用基本不等式证明不等式
【解题方法总结】类似于基本不等式的结构的不等式的证明可以利用基本不等式去组合、分解、运算获得证明．
题型九：利用基本不等式解决实际问题
【解题方法总结】1、理解题意，设出变量，建立函数模型，把实际问题抽象为函数的最值问题．2、注意定义域，验证取得条件．3、注意实际问题隐藏的条件，比如整数，单位换算等．
题型十：与?+?、平方和、??有关问题的最值
【解题方法总结】利用基本不等式变形求解