山东省聊城市东阿县姜楼中学2023-2024学年七年级下学期3月月考数学试题

这是一份山东省聊城市东阿县姜楼中学2023-2024学年七年级下学期3月月考数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.如图，学校相对于小明家的位置下列描述最准确的是( )
A. 距离学校1200米处B. 北偏东65∘方向上的1200米处
C. 南偏西65∘方向上的1200米处D. 南偏西25∘方向上的1200米处
2.已知∠AOB=50°，∠BOC=30°，OD平分∠AOC，则∠AOD的度数为( )
A. 20°B. 80°C. 20°或80°D. 10°或40°
3.若角α的补角等于120°，则角α的余角为( )
A. 10°B. 20°C. 30°D. 60°
4.已知∠1+∠2=180°且∠2=∠3，则∠3+∠1=180°，依据是( )
A. 等角的补角相等B. 同角的补角相等C. 等量代换D. 补角的定义
5.如图，直线a，b相交于点O，如果∠1+∠2=60°，那么∠3是( )
A. 150°B. 120°C. 60°D. 30°
6.在同一平面内，若AB⊥l，AC⊥l，且点A在直线l上，则下列结论成立的是 ( )
A. AC//ABB. 点B，C在直线l同侧
C. 点B，C在直线l两侧D. 点A，B，C在同一条直线上
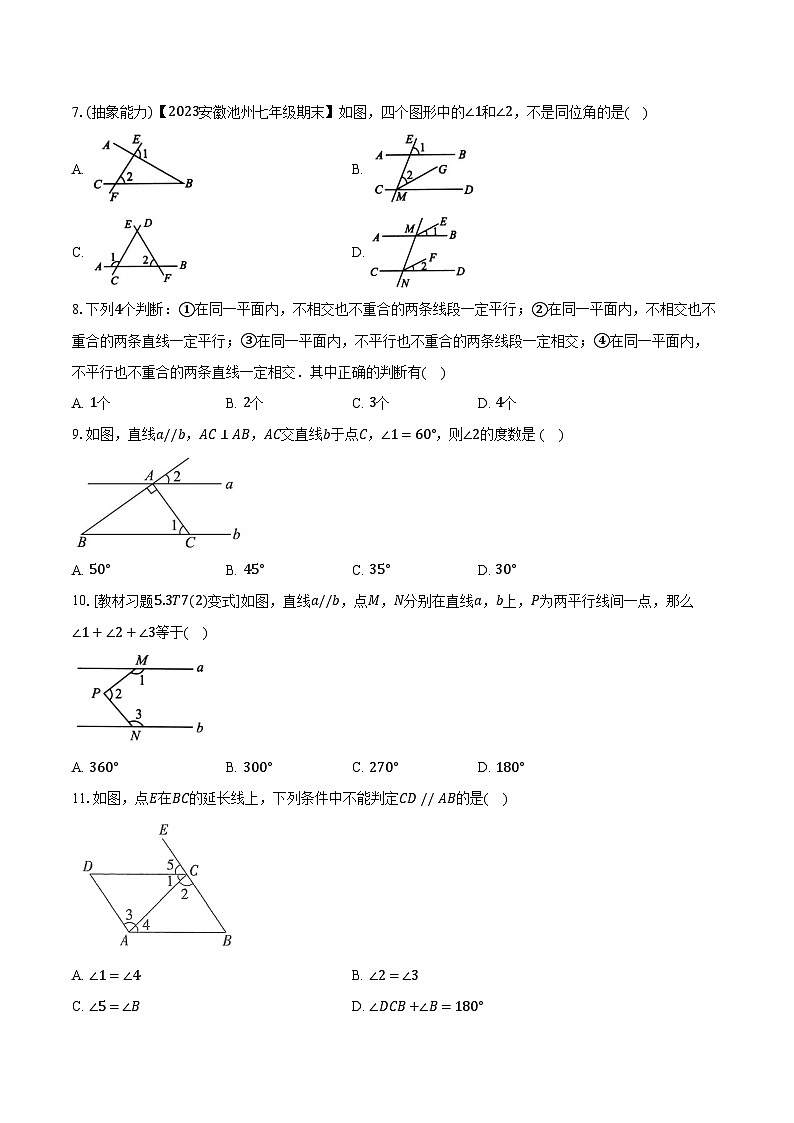
7.(抽象能力)【2023安徽池州七年级期末】如图，四个图形中的∠1和∠2，不是同位角的是( )
A. B.
C. D.
8.下列4个判断：①在同一平面内，不相交也不重合的两条线段一定平行；②在同一平面内，不相交也不重合的两条直线一定平行；③在同一平面内，不平行也不重合的两条线段一定相交；④在同一平面内，不平行也不重合的两条直线一定相交．其中正确的判断有( )
A. 1个B. 2个C. 3个D. 4个
9.如图，直线a//b，AC⊥AB，AC交直线b于点C，∠1=60°，则∠2的度数是 ( )
A. 50°B. 45°C. 35°D. 30°
10.[教材习题5.3T7(2)变式]如图，直线a//b，点M，N分别在直线a，b上，P为两平行线间一点，那么∠1+∠2+∠3等于( )
A. 360°B. 300°C. 270°D. 180°
11.如图，点E在BC的延长线上，下列条件中不能判定CD // AB的是( )
A. ∠1=∠4B. ∠2=∠3
C. ∠5=∠BD. ∠DCB+∠B=180°
12.如图，∠A的一边AB为平面镜，另一边AC上有一点D，从D点射出一束光线经AB上一点E反射，反射光线EF恰好与AC平行，已知∠AED=∠BEF，∠EDC=70°，则∠A的度数是( )
A. 30°B. 35°C. 40°D. 45°
二、填空题：本题共5小题，每小题3分，共15分。
13.张师傅晚上出门散步，出门时6点多一点，他看到手表上的分针与时针的夹角恰好为120°，回来时接近7点，他又看了一下手表，发现此时分针与时针再次成120°，则张师傅此次散步的时间是______分钟．
14.如图，直线EF，CD相交于点O，OA⊥OB，OD平分∠AOF，若∠FOD=4∠COB，则∠AOE=______．
15.如图，直线a/​/b，△ABC的顶点A和C分别落在直线a和b上，若∠1=60°，∠ACB=40°，则∠2的度数是______．
16.如图，把一张长方形纸条ABCD沿EF折叠，若∠1=62°，则∠AEG= °.
17.(泰州中考)如图，木棒AB，CD与EF分别在G，H处用可旋转的螺丝铆住，∠EGB=100°，∠EHD=80°，将木棒AB绕点G逆时针旋转到与木棒CD平行的位置，则至少要旋转__________°．
三、解答题：本题共8小题，共69分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题5分)
如图，A，O，B三点共线，∠1:∠2:∠3=1:3:2，求∠BOC的度数．
19.(本小题5分)
如图，∠AOB是平角，∠DOE=90°，OC平分∠DOB，OD平分∠AOC．
求∠AOE的度数．
20.(本小题9分)
解答下列各题

(1)如图，在∠AOB中，以O为顶点引射线，填表：
(2)若∠AOB内射线的条数是n，请用关于n的式子表示出上面的结论．
(3)若∠AOB内有射线条数是2024，则角的总个数为多少？
21.(本小题9分)
有公共顶点的两个角，∠AOB=∠COD，且OE为∠BOC的角平分线．
(1)如图1，请探索∠AOE和∠DOE的大小关系，并说明理由；
(2)如图2，∠AOE和∠DOE是否仍然满足(1)中关系？请说明理由；
(3)若∠AOB=90°，∠AOC=64°，求出∠BOE的度数．
22.(本小题10分)
直线AB、CD相交于点O，∠EOF在∠AOD的内部．
(1)如图①，当∠AOD=150°，∠EOF=30°时，求∠AOF与∠EOD的度数和；
(2)在(1)的条件下，请直接写出图中与∠BOC互补的角；
(3)如图②，若射线OM平分∠AOD(OM在∠EOD内部)，且满足∠EOD=2∠FOM，请判断∠AOF与∠EOF的大小关系并说明理由．
23.(本小题10分)
如图，MN // BC，BD⊥DC，∠1=∠2=60°，DC是∠NDE的平分线．
(1) AB与DE平行吗？请说明理由．
(2)试说明∠ABC=∠C．
(3)求∠ABD的度数．
24.(本小题10分)
如图，已知点A在EF上，点P，Q在BC上，∠E=∠EMA，∠BQM=∠BMQ．
(1)试说明：EF//BC；
(2)若FP⊥AC，∠2+∠C=90°，试说明：∠1=∠B；
(3)若∠3+∠4=180°，∠BAF=3∠F-20°，求∠B的度数．
25.(本小题12分)
【提出问题】若两个角的两边分别平行，则这两个角有怎样的数量关系？
【解决问题】分两种情况进行探究，请结合图形探究这两个角的数量关系．
(1)如图1，AB//EF，BC//DE.试说明：∠1=∠2．
(2)如图2，AB//EF，BC//DE.试说明：∠1+∠2=180°．
(3) 【得出结论】由(1)(2)我们可以得到结论：若两个角的两边分别平行，则这两个角的数量关系为_____________．
(4) 【拓展应用】若两个角的两边分别平行，其中一个角比另一个角的2倍少60°，求这两个角的度数．
七年级水平调研数学试题答案
1. B 2. D 3. C 4. C 5. A 6. D 7. D
8. B 9. D 10. A 11. B 12. B
13. 48011
14. 36°
15. 20°
16. 56
17. 20
18. 120°
19. 解：∵OC平分∠DOB，
∴∠BOC=∠COD，
∵OD平分∠AOC，
∴∠AOD=∠COD，
∴∠AOD=∠COD=∠BOC．
∴∠AOD+∠COD+∠BOC=∠AOB=180°．
∴∠AOD=60°，
∵∠DOE=90°，
∴∠AOE=∠DOE-∠AOD=30°．
20. 解：(1)如表：
(2)若∠AOB内射线的条数是n，角的总个数=12(n+1)(n+2)；
(3)把n=2024代入12(n+1)(n+2)可得
12(2024+1)(2024+2)=2051325(个)，
即角的总个数为2051325．
21. 解：(1)∠AOE=∠DOE，理由如下：
∵OE为∠BOC的角平分线，
∴∠BOE=∠COE．
∵∠AOB=∠COD，
∴∠AOB+∠BOE=∠COD+∠COE．
∴∠AOE=∠DOE．
(2)∠AOE=∠DOE，理由如下：
∵OE为∠BOC的角平分线，
∴∠BOE=∠COE．
∵∠AOB=∠COD，
∴∠AOB-∠BOE=∠COD-∠COE．
∴∠AOE=∠DOE．
(3)当OC在∠AOB内，如图2
∵∠AOB=90°，∠AOC=64°，
∴∠AOB-∠AOC=26°．
∵OE为∠BOC的角平分线，
∴∠BOE=12∠BOC=13°．
当当OC在∠AOB外，如图3
∵∠AOB=90°，∠AOC=64°
∴∠BOC=∠AOB+∠AOC=154°
∵OE为∠BOC的角平分线，
∴∠BOE=12∠BOC=77°
综上，∠BOE=13°或77°．
22. 解：(1)∵∠DOE+∠EOF+∠AOF=∠AOD=150°且∠EOF=30°，
∴∠DOE+∠AOF=∠150°-30°=120°；
(2)∠BOD、∠AOC、∠EOF；
(3)∠AOF=∠EOF，理由如下：
∵OM平分∠AOD，
∴∠DOM=∠AOM，
∴∠AOF=∠AOM-∠FOM
=∠DOM-∠FOM
=∠EOD-∠MOE-∠FOM
=2∠FOM-∠MOE-∠FOM
=∠FOM-∠MOE
=∠EOF，
∴∠AOF=∠EOF．
23. 【小题1】
AB // DE.理由：∵MN // BC，∠1=60°，∴∠ABC=∠1=60°．
∵∠1=∠2，∴∠ABC=∠2.∴AB // DE．
【小题2】
证明：∵MN // BC，∴∠NDE+∠2=180°．
∴∠NDE=180°-∠2=180°-60°=120°．
∵DC是∠NDE的平分线，∴∠EDC=∠NDC=12∠NDE=60∘．
∵MN // BC，∴∠C=∠NDC=60°．
∵∠ABC=60°，∴∠ABC=∠C．
【小题3】
∵∠ADC+∠NDC=180°，∠NDC=60°，
∴∠ADC=180°-∠NDC=180°-60°=120°．
∵BD⊥DC，∴∠BDC=90°．
∴∠ADB=∠ADC-∠BDC=120°-90°=30°．
∵MN // BC，∴∠DBC=∠ADB=30°．
∵∠ABC=60°，∴∠ABD=60°-30°=30°．

24. 【小题1】解：∵∠E=∠EMA，∠BQM=∠BMQ，∠EMA=∠BMQ，
∴∠E=∠BQM，
∴EF // BC．
【小题2】解：∵FP⊥AC，
∴∠PGC=90°．
∵EF // BC，
∴∠EAC+∠C=180°．
∵∠2+∠C=90°，
∴∠BAC=∠PGC=90°，
∴AB // FP，
∴∠1=∠B．
【小题3】解：∴∠3+∠4=180°，∠4=∠MNF，
∴∠3+∠MNF=180°，
∴AB // FP，
∴∠F+∠BAF=180°．
∵∠BAF=3∠F-20°，
∴∠F+3∠F-20°=180°，
解得∠F=50°．
∵AB // FP，EF // BC，
∴∠B=∠1，∠1=∠F，
∴∠B=∠F=50°．
25. 【小题1】
证明：∵AB // EF，
∴∠1=∠3．
∵BC // DE，
∴∠2=∠3．
∴∠1=∠2．
【小题2】
证明：∵AB // EF，
∴∠1=∠4．
∵BC // DE，
∴∠2+∠4=180°．
∴∠1+∠2=180°．
【小题3】
相等或互补
【小题4】
解：设其中一个角的度数为x°，则另一角的度数为(2x-60)°．
①当x=2x-60时，
解得x=60．
此时两个角的度数分别为60°，60°；
②当x+2x-60=180，
解得x=80．
则2x-60=100．
此时两个角的度数分别为80°，100°．
综上所述，这两个角的度数为60°，60°或80°，100°．

∠AOB内射线的条数
1
2
3
4
角的总个数
______
______
______
______
∠AOB内射线的条数
1
2
3
4
角的总个数
3
6
10
15