




【考前50天】最新高考数学重点专题三轮冲刺演练 专题03 立体几何大题 (基础练)
展开1、多加总结。当三年所有的数学知识点加在一起,可能会使有些基础不牢固的学生犯迷糊。
2、做题经验。哪怕同一题只改变数字,也能成为一道新的题目。
3、多刷错题。多刷错题能够进一步地扫清知识盲区,多加巩固之后自然也就掌握了知识点。
对于学生来说,三轮复习就相当于是最后的“救命稻草”,家长们同样是这样,不要老是去责怪孩子考试成绩不佳,相反,更多的来说,如果能够陪同孩子去反思成绩不佳的原因,找到问题的症结所在,更加重要。
【一专三练】 专题03 立体几何大题基础练-新高考数学复习分层训练(新高考通用)
1.(2022·河北·校联考模拟预测)在斜三棱柱中,是等腰直角三角形,,平面底面,.
(1)证明:;
(2)求二面角的正弦值.
2.(2023·浙江金华·浙江金华第一中学校考模拟预测)如图,在直三棱柱中,,,,M为的中点.
(1)证明:平面;
(2)求点A到平面的距离.
3.(2023·江苏泰州·统考一模)如图,在中,是边上的高,以为折痕,将折至的位置,使得.
(1)证明:平面;
(2)若,求二面角的正弦值.
4.(2023·辽宁阜新·校考模拟预测)如图,在等腰直角三角形ABC中(如图1),∠A=90°,点E,F分别是AB,BD的中点,将△ABC沿AD折叠得到图2所示图形,设是平面EFC和平面ACD的交线.
(1)求证:⊥平面BCD;
(2)求平面ACD和平面BCD夹角的余弦值.
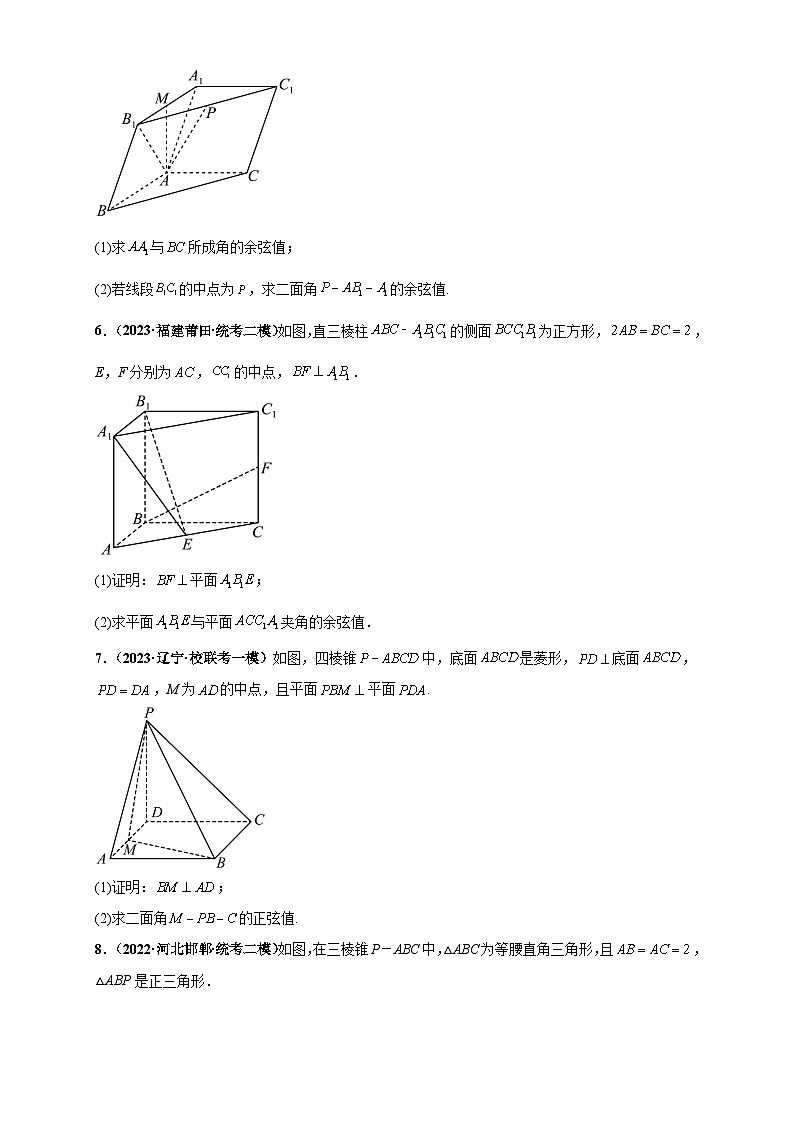
5.(2023·江苏南通·统考模拟预测)三棱柱中,,,线段的中点为,且.
(1)求与所成角的余弦值;
(2)若线段的中点为,求二面角的余弦值.
6.(2023·福建莆田·统考二模)如图,直三棱柱的侧面为正方形,,E,F分别为,的中点,.
(1)证明:平面;
(2)求平面与平面夹角的余弦值.
7.(2023·辽宁·校联考一模)如图,四棱锥中,底面是菱形,底面,,M为的中点,且平面平面.
(1)证明:;
(2)求二面角的正弦值.
8.(2022·河北邯郸·统考二模)如图,在三棱锥P-ABC中,△ABC为等腰直角三角形,且,△ABP是正三角形.
(1)若,求证:平面ABP⊥平面ABC;
(2)若直线PC与平面ABC所成角为,求二面角的余弦值.
9.(2023·江苏·统考一模)在三棱柱中,平面平面,侧面为菱形,,,,E是的中点.
(1)求证:平面;
(2)点P在线段上(异于点,),与平面所成角为,求的值.
10.(2022·山东·潍坊一中校考模拟预测)在如图所示的多面体AFDCBE中,平面BCE,,,,,.
(1)在线段BC上是否存在一点G,使得平面AFC?如果存在,请指出G点位置并证明;如果不存在,请说明理由;
(2)当三棱锥的体积为8时,求二面角的余弦值.
11.(2022·山东日照·校联考二模)如图,等腰梯形ABCD中,,,现以AC为折痕把折起,使点B到达点P的位置,且.
(1)证明:平面平面ADC;
(2)若M为PD上一点,且三棱锥的体积是三棱锥体积的2倍,求二面角的余弦值.
12.(2022·湖北武汉·武汉二中校考模拟预测)如图(1),平面四边形中,,,,将沿边折起如图(2),使,点,分别为,中点.
(1)判断直线与平面的位置关系,并说明理由;
(2)求二面角的正弦值.
13.(2022·湖北·校联考模拟预测)如图,四棱台中,上底面是边长为1的菱形,下底面ABCD是边长为2的菱形,平面ABCD且
(1)求证:平面平面;
(2)若直线AB与平面所成角的正弦为,求棱台的体积.
14.(2022·湖北宜昌·宜昌市夷陵中学校考模拟预测)如图,三棱柱中,点在平面内的射影在上,,.
(1)证明:;
(2)若,求二面角的余弦值.
15.(2022·湖北十堰·丹江口市第一中学校考模拟预测)如图,在多面体中,四边形是边长为2的正方形,.
(1)求证:平面平面;
(2)求平面与平面所成锐角的余弦值.
16.(2022·湖南岳阳·统考三模)如图,在四棱锥中,底面是菱形,是的中点.
(1)证明:平面;
(2)若直线平面,,且与平面所成的角正弦值为,求锐二面角的余弦值.
17.(2022·湖南·校联考模拟预测)如图,在直三棱柱中,,,点为棱的中点,点为线段上的一动点.
(1)求证:当点为线段的中点时,平面;
(2)当点位于线段的什么位置时,与平面所成角的正弦值为,请说明理由.
18.(2022·湖南长沙·长郡中学模拟预测)如图,已知直三棱柱,,,分别为线段,,的中点,为线段上的动点,,.
(1)若,试证;
(2)在(1)的条件下,当时,试确定动点的位置,使线段与平面所成角的正弦值为
19.(2023·湖南长沙·雅礼中学校考模拟预测)如图,在三棱锥中,已知,是的中点.
(1)求证:平面平面;
(2)若,求平面与平面夹角的正弦值.
20.(2022·湖南长沙·长郡中学校考模拟预测)已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点,.
(1)证明:;
(2)求当面与面所成的二面角的正弦值最小时,三棱锥的体积.
21.(2022·广东·统考模拟预测)如图,已知, ,,平面⊥平面, ,,F为的中点.
(1)证明:平面;
(2)求平面与平面所成锐二面角的余弦值.
22.(2022·江苏·统考二模)如图,在四棱锥中,四边形是边长为2的菱形,是边长为2的等边三角形,,.
(1)求证:平面平面;
(2)求平面和平面所成锐二面角的大小.
23.(2022·江苏南通·校联考模拟预测)如图,在四棱锥P-ABCD中,底面ABCD是4长为的正方形,侧面PAD⊥底面ABCD,M为PA的中点,PA=PD=.
(1)求证:PC∥平面BMD;
(2)求二面角M-BD-P的大小.
24.(2022·江苏徐州·统考模拟预测)如图,在三棱锥中,平面平面,,O为的中点,.
(1)证明:平面;
(2)点E在棱上,若,二面角的大小为,求实数的值.
25.(2022·江苏泰州·统考模拟预测)如图,在正三棱柱中,,,为的中点,为侧棱上的点.
(1)当为的中点时,求证:平面;
(2)若平面与平面所成的锐二面角为,求的长度.
26.(2022·江苏常州·华罗庚中学校联考三模)如图,ABCD是边长为6的正方形,已知,且并与对角线DB交于G,H,现以ME,NF为折痕将正方形折起,且BC,AD重合,记D,C重合后为P,记A,B重合后为Q.
(1)求证:平面平面HGQ;
(2)求平面GPN与平面GQH所成二面角的正弦值.
27.(2022·海南省直辖县级单位·校联考一模)如图,在三棱台中,已知平面平面,,,
(1)求证:直线平面;
(2)求平面与平面所成角的正弦值.
28.(2023·广东惠州·统考模拟预测)如图,在四棱锥P-ABCD中,底面ABCD为正方形,底面ABCD,,E为线段PB的中点,F为线段BC上的动点.
(1)证明:平面平面PBC;
(2)若直线AF与平面PAB所成的角的余弦值为,求点P到平面AEF的距离.
29.(2023·安徽蚌埠·统考二模)如图,正方体的棱长为1,E,F是线段上的两个动点.
(1)若平面,求的长度;
(2)若,求直线与平面所成角的正弦值.
30.(2023·山东·沂水县第一中学校联考模拟预测)已知多面体中,四边形是边长为4的正方形,四边形是直角梯形,,,.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
【考前50天】最新高考数学重点专题三轮冲刺演练 专题02 三角函数与解三角形大题 (压轴练): 这是一份【考前50天】最新高考数学重点专题三轮冲刺演练 专题02 三角函数与解三角形大题 (压轴练),文件包含专题02三角函数与解三角形大题压轴练原卷版docx、专题02三角函数与解三角形大题压轴练解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
【考前50天】最新高考数学重点专题三轮冲刺演练 专题02 三角函数与解三角形大题 (基础练): 这是一份【考前50天】最新高考数学重点专题三轮冲刺演练 专题02 三角函数与解三角形大题 (基础练),文件包含专题02三角函数与解三角形大题基础练原卷版docx、专题02三角函数与解三角形大题基础练解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
【考前50天】最新高考数学重点专题三轮冲刺演练 专题01 数列大题 (压轴练): 这是一份【考前50天】最新高考数学重点专题三轮冲刺演练 专题01 数列大题 (压轴练),文件包含专题01数列大题压轴练原卷版docx、专题01数列大题压轴练解析版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。












