专题07 简单几何证明题(三角形全等、特殊四边形判定、与相似有关的证明)-备战2024年中考数学一轮复习重难题型（全国通用）

这是一份专题07 简单几何证明题(三角形全等、特殊四边形判定、与相似有关的证明)-备战2024年中考数学一轮复习重难题型（全国通用），文件包含专题07简单几何证明题三角形全等特殊四边形判定与相似有关的证明原卷版docx、专题07简单几何证明题三角形全等特殊四边形判定与相似有关的证明解析版docx等2份试卷配套教学资源，其中试卷共80页， 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
专题07简单几何证明题
(三角形全等、特殊四边形判定及性质、与相似有关的证明)
类型一三角形全等
1．（2023·江西·统考中考真题）（1）如图，，平分．求证：．

2．（2023·江苏苏州·统考中考真题）如图，在中，为的角平分线．以点圆心，长为半径画弧，与分别交于点，连接．

(1)求证：；
(2)若，求的度数．
3．（2023·云南·统考中考真题）如图，是的中点，．求证：．

4．（2023·四川宜宾·统考中考真题）已知：如图，，，．求证：．

5．（2023·福建·统考中考真题）如图，．求证：．
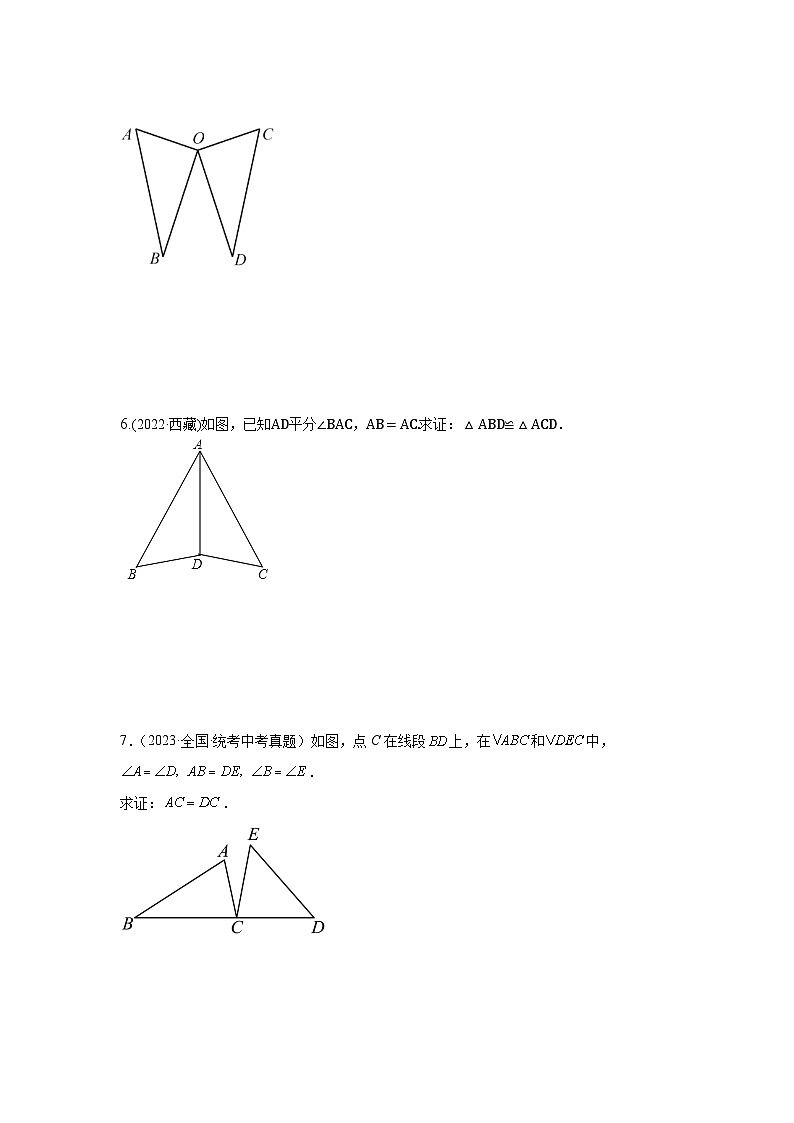
6.(2022·西藏)如图，已知AD平分∠BAC，AB=AC.求证：△ABD≌△ACD．
7．（2023·全国·统考中考真题）如图，点C在线段上，在和中，．
求证：．

8．（2023·四川乐山·统考中考真题）如图，AB、CD相交于点O，AO=BO，AC∥DB．求证：AC=BD．
9.(2022·江苏省南通市)如图，AC和BD相交于点O，OA=OC，OB=OD．
(1)求证：∠A=∠C；
(2)求证：AB//CD．
10．（2023·山东聊城·统考中考真题）如图，在四边形中，点E是边上一点，且，．

(1)求证：；
(2)若，时，求的面积．
11.(2022·贵州省铜仁市)如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB=CD.求证：△ABC≌△CDE．
12.(2022·广东省云浮市)如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E.求证：△OPD≌△OPE．
13.(2022·四川省宜宾市)已知：如图，点A、D、C、F在同一直线上，AB/​/DE，∠B=∠E，BC=EF.求证：AD=CF．
14.(2022·陕西省)如图，在△ABC中，点D在边BC上，CD=AB，DE/​/AB，∠DCE=∠A.求证：DE=BC．
15.(2022·湖南省衡阳市)如图，在△ABC中，AB=AC，D、E是BC边上的点，且BD=CE.求证：AD=AE．
16.(2022·四川省乐山市)如图，B是线段AC的中点，AD/​/BE，BD//CE.求证：△ABD≌△BCE．
17.（2021·湖南衡阳市·中考真题）如图，点A、B、D、E在同一条直线上，．求证：．
18.（2021·四川乐山市·中考真题）如图，已知，，与相交于点，求证：．
19.（2021·四川泸州市·中考真题）如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C，求证：BD=CE
20.（2021·云南中考真题）如图，在四边形中，与相交于点E．求证：．
21.（2020•菏泽）如图，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D，若BC＝ED，求证：CE＝DB．
22.（2020•南充）如图，点C在线段BD上，且AB⊥BD，DE⊥BD，AC⊥CE，BC＝DE．求证：AB＝CD．
23.（2020•铜仁市）如图，∠B＝∠E，BF＝EC，AC∥DF．求证：△ABC≌△DEF．
24.（2020•台州）如图，已知AB＝AC，AD＝AE，BD和CE相交于点O．
（1）求证：△ABD≌△ACE；
（2）判断△BOC的形状，并说明理由．
25.如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．
（1）求证：AB＝CD；
（2）若AB＝CF，∠B＝40°，求∠D的度数．
类型二特殊四边形判定及性质
26．（2023·湖南怀化·统考中考真题）如图，矩形中，过对角线的中点作的垂线，分别交，于点，．

(1)证明：；
(2)连接、，证明：四边形是菱形．
27．（2023·湖北随州·统考中考真题）如图，矩形的对角线，相交于点O，．

(1)求证：四边形是菱形；
(2)若，求四边形的面积．
28.(2022·广西壮族自治区河池市)如图，点A，F，C，D在同一直线上，AB=DE，AF=CD，BC=EF．
(1)求证：∠ACB=∠DFE；
(2)连接BF，CE，直接判断四边形BFEC的形状．
29．（2023·湖南永州·统考中考真题）如图，已知四边形是平行四边形，其对角线相交于点O，．

(1)是直角三角形吗？请说明理由；
(2)求证：四边形是菱形．
30．（2023·新疆·统考中考真题）如图，和相交于点，，．点、分别是、的中点．

(1)求证：；
(2)当时，求证：四边形是矩形．
31.(2022·青海省西宁市)如图，四边形ABCD是菱形，AE⊥BC于点E，AF⊥CD于点F．
(1)求证：△ABE≌△ADF；
(2)若AE=4，CF=2，求菱形的边长．
32．（2023·云南·统考中考真题）如图，平行四边形中，分别是的平分线，且分别在边上，．

(1)求证：四边形是菱形；
(2)若，的面积等于，求平行线与间的距离．
33．（2023·浙江嘉兴·统考中考真题）如图，在菱形中，于点，于点，连接

(1)求证：；
(2)若，求的度数．
34.(2022·江苏省无锡市)如图，已知四边形ABCD为矩形，AB=22，BC=4，点E在BC上，CE=AE，将△ABC沿AC翻折到△AFC，连接EF．
(1)求EF的长；
(2)求sin∠CEF的值．
35．（2023·湖南张家界·统考中考真题）如图，已知点A，D，C，B在同一条直线上，且，，．

(1)求证：；
(2)若时，求证：四边形是菱形．
36.(2022·湖北省荆门市)如图，已知矩形ABCD中，AB=8，BC=x(0