2023年山东聊城市中考数学模拟预测题(3)（无答案）

这是一份2023年山东聊城市中考数学模拟预测题(3)（无答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
时间：120分钟 分值120分
一、选择题（本大题共12个小题，每小题3分。在每小题给出的四个选项中，只有一项是符合题目要求）
1．下列各数中，绝对值最小的数是（ ）
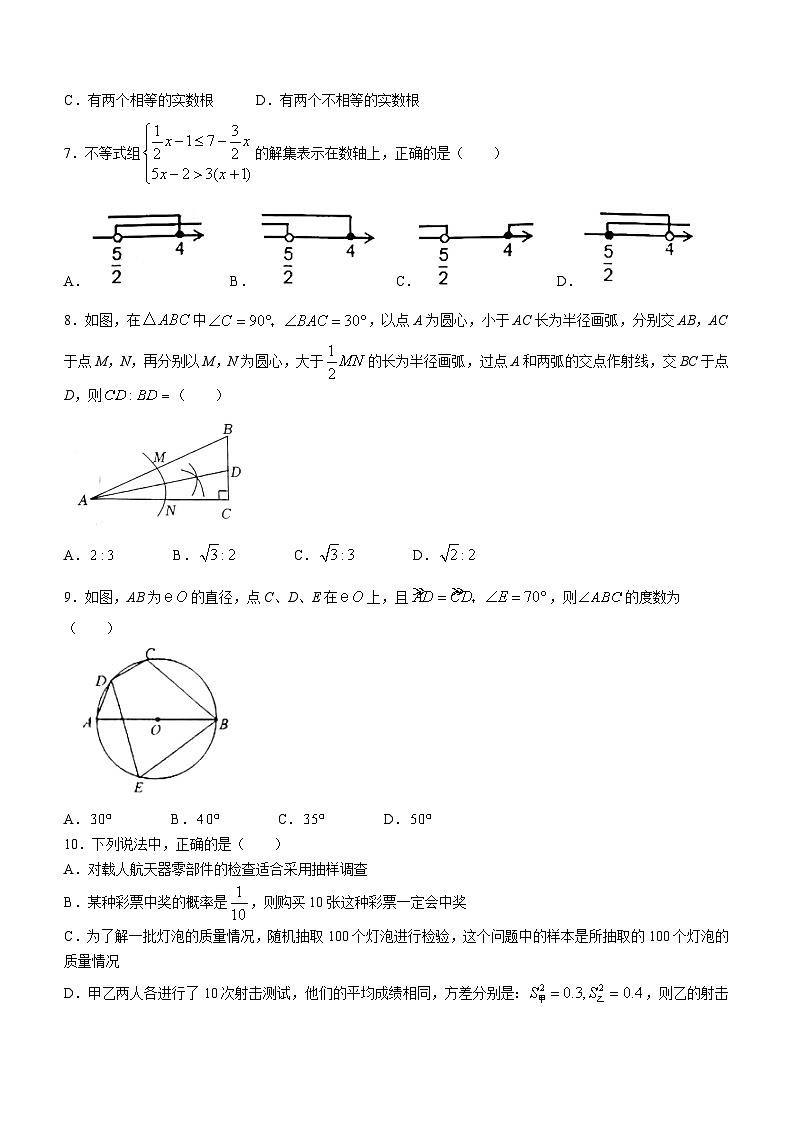
A． B． C． D．0
2．将两个大小完全相同的杯子（如图甲）叠放在一起（如图乙），则图乙中实物的俯视图是（ ）
图甲 图乙
A． B． C． D．
3．2023年2月，中国旅游研究院发布的《中国旅游经济蓝皮书》预测，2023年我国国内旅游人数将达到45.5亿人次，同比增长约，恢复到2019年的；实现国内旅游收入约4万亿元，同比增长约，恢复到2019年的．将45.5亿用科学记数法表示应为（ ）
A．B．C．D．
4．如图，直线，的顶点C在直线a上，AB与直线a交于点D，CB延长线交直线b于点E，己知，则的度数是（ ）
A． B． C． D．
5．下列运算正确的是（ ）
A． B． C． D．
6．方程的根的情况是（ ）
A．没有实数根 B．只有一个实数根
C．有两个相等的实数根 D．有两个不相等的实数根
7．不等式组的解集表示在数轴上，正确的是（ ）
A． B． C． D．
8．如图，在中，以点A为圆心，小于AC长为半径画弧，分别交AB，AC于点M，N，再分别以M，N为圆心，大于的长为半径画弧，过点A和两弧的交点作射线，交BC于点D，则（ ）
A． B． C． D．
9．如图，AB为的直径，点C、D、E在上，且，则的度数为（ ）
A． B． C． D．
10．下列说法中，正确的是（ ）
A．对载人航天器零部件的检查适合采用抽样调查
B．某种彩票中奖的概率是，则购买10张这种彩票一定会中奖
C．为了解一批灯泡的质量情况，随机抽取100个灯泡进行检验，这个问题中的样本是所抽取的100个灯泡的质量情况
D．甲乙两人各进行了10次射击测试，他们的平均成绩相同，方差分别是：，则乙的射击成绩较稳定
11．对于实数a、b，定义一种新运算“※”：，这里等式右边是实数运算．例如：，则方程的解是（ ）
A． B． C． D．
12．如图1，点P从的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M是曲线部分的最低点，则的面积是（ ）
图1 图2
A．12 B．24 C．36 D．48
二、填空题（本题共5个小题，每小题3分，共15分。只要求填写最后结果）
13．分解因式：_________．
14．将一个圆心角为120，半径为的扇形围成一个圆锥的侧面，则所得圆锥的高为_______．
15．一组数据：1，3，a，5，7的平均数是a，则它们的方差是_________．
16．如图，在扇形BOC中，，点D为弧BC的中点，点E为半径OB上一动点，若，则阴影部分周长的最小值为_________．
17．在平面直角坐标系中，等边如图放置，点A的坐标为，每一次将绕着点O逆时针方向旋转，同时每边扩大为原来的2倍，第一次旋转后得到，第二次旋转后得到，依次类推，则点的坐标为_________．
三、解答题（本题共8个小题，共69分。解答应写出文字说明、证明过程或演算步骤）
18．（本小题7分）先化简，再求代数式的值，其中．
19．（本小题8分）中国共产党的助手和后备军一一中国共青团，担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务．在中国共青团成立一百周年之际，我县各中小持续开展了A：青年大学习；B：学党史；C：中国梦宣传教育；D社会主义核心价值观培育践行等一系列活动，学生可以任选一项活动参加．为了解学生参与活动的情况，在全县范围内进行了一次抽样调查，根据收集的数据绘制了如下两幅不完整的统计图．
请根据图中提供的信息，解答下列问题：
（1）在这次抽样调查中，一共抽取了_________名学生；
（2）补全条形统计图；
（3）陈杰和刘慧两位同学参加了上述活动，请用列表或画树状图的方法，求出她们俩参加同一项活动的概率．
20．（本小题8分）如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作于点E，延长BC到点F，，使，连接DF．
（1）求证：四边形AEFD是矩形；
（2）连接OE，若，求OE的长度．
21．（本小题8分）2022年11月29日，“神舟十五号”载人航天飞船搭载“明星”机械臂成功发射．2023年2月9日神舟十五号航天员进行了出舱活动，为了确保任务的圆满完成，航天员借助机械臂进行舱外作业．如图是处于工作状态的某型号手臂机器人示意图，OA是垂直于工作台的移动基座，AB、BC为机械臂，，．
（1）求机械臂端点C到工作台的距离CD的长；（结果精确到）
（2）求OD的长．（结果精确到）
（参考数据：）
22．（体小题8分）某餐饮公司推出甲、乙两种外卖菜品，已知售出2份甲菜品和1份乙菜品可获利40元，售出3份甲菜品和2份乙菜品可获利65元．
（1）求每份甲、乙菜品的利润各是多少元？
（2）根据营销情况，该餐饮公司每日都可以销售完甲、乙两种外卖菜品600份，且甲菜品的数量不多于乙菜品的一半，应该如何设计两种菜品的数量才能使获得的利润最高？最高利润是多少？
23．（本小题8分）如图，已知，反比例函数的图象过点，反比例函数的图象过点A．
（1）求a和k的值；
（2）过点B作轴，与双曲线交于点C．求的面积．
24．（本小题10分）如图，在中，．延长OA至点C，使，连接BC，以O为圆心，OB长为半径作，延长BA，与交于点E，作弦，连接EF，与BO的延长线交于点D．
（1）求证：BC是的切线；
（2）求EF的长．
25．（本小题12分）如图，抛物线与x轴交于点与y轴交于点C，连接BC．
备用图
（1）求该抛物线的解析式；
（2）点D是直线BC上方的抛物线上一点，连接OD交BC于点E，当时，求点D的坐标；
（3）点P在抛物线的对称轴上，在坐标平面内是否存在点Q，使得以P，Q，B，C为顶点的四边形是矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
二O二三年聊城市初中学生学业水平仿真考试
数学试题答案
一、选择题
二、填空题
13． 14． 15．4 16． 17．
三、解答题
18．解：原式， 4分
， 6分
原式． 7分
19．（1）在这次调查中，一共抽取的学生为：（名），
故答案为：200； 2分
（2）C的人数为：（名）， 3分
补全条统计图如下： 4分
（3）画树状图如下：
6分
共有16种等可能的结果，其中陈本杰和刘慧参加同一项活动的结果有4种，
∴小杰和小慧参加同一项活动的概率为． 8分
20．解：（1）正明：四边形ABCD是菱形，
且，
，
，
四边形AEFD是平行四边形， 3分
，
四边形AEFD是矩形； 4分
（2）解：四边形ABCD是菱形，，
，
， 6分
在中，，
在中，， 7分
四边形ABCD是菱形，
，
． 8分
21．解：（1）过点B作于点E，过点B作于点F，过点A作AG于点G，
∴四边形BEDF是矩形，四边形AOFG是矩形，
米，
，
米，米， 2分
在中，，
米，米，
米， 4分
答：机械臂端点C到工作台的距离CD的长6.6米．
（2）在中，由勾股定理可知：米，
在中，
由勾股理可知：米， 6分
米，米．
答：OD的长为3.8米． 8分
22．解：（1）解：（1）设每份菜品A的利润为x元，每份菜品B的润为y元，
根据题意得， 2分
解得，
答：每份菜品甲的利润伪15元，每份菜品乙的利润为10元； 4分
（2）设购进钾菜品m份，总利润为w元，
根据题意得，
解得， 5分
， 6分
，w随着m的增大而增大，
当时，w取得最大值，最大值为7000元，
（份）， 8分
答：购进甲菜品400份，乙菜品200份，所获利润最大，最大利润为1700元．
23．解：（1）比例函数的图象过点，
， 2分
分过点A、B作轴于D，轴于E，
，
，
，
，
， 3分
反比例函数的图象过点A， 4分
（2）由（1）可知，
轴，，点的纵坐标为1，
过点C作轴于F，
点C在双曲线上，，解得，
， 6分
． 8分
24．（1）证明：，
，
，
，
即， 3分
为的半径，BC是的切线； 5分
（2）解：如图，过点O作于点G，
，弦，
，
， 6分
，即BD平分，
，即为等腰三角形，，
，
在中，，
在中，，
． 8分
25．解：（1）把代入得：
解得：，
； 3分
（2）过E作轴于K，如图：
在中，令得，
由得直线BC解析式为，
，，
，
在中，令得，
，∴直线OD解析式为， 5分
解得：或（舍去）．； 7分
（3）在坐标平面内存在点Q，使得以P，Q，B，C为顶点的四边形是矩形，理由如下：
由得抛物线的对称轴是直线，
设，又，
①若PQ，BC是对角线，则PQ，BC中点重合且，
，解得或，
或； 9分
②若PB，QC为对角线，同理得：
，解得，
， 10分
③若PC，QB是对角线，
，解得，
，
综上所述，Q的坐标为或或或．
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
A
C
B
D
A
B
B
C
A
D