



- 专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题04 二倍角的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题06 正弦定理、余弦定理及其应用(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题07 复数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 0 次下载
- 专题09 基本图形的平行与垂直(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 0 次下载
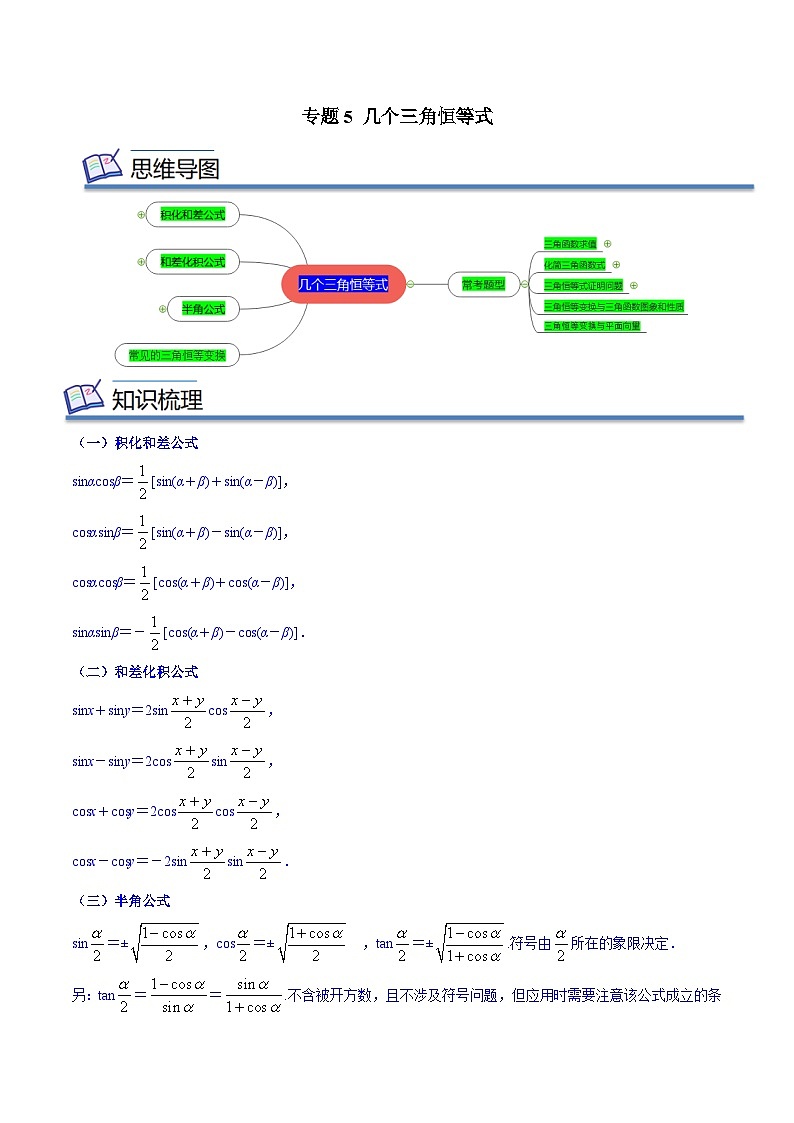
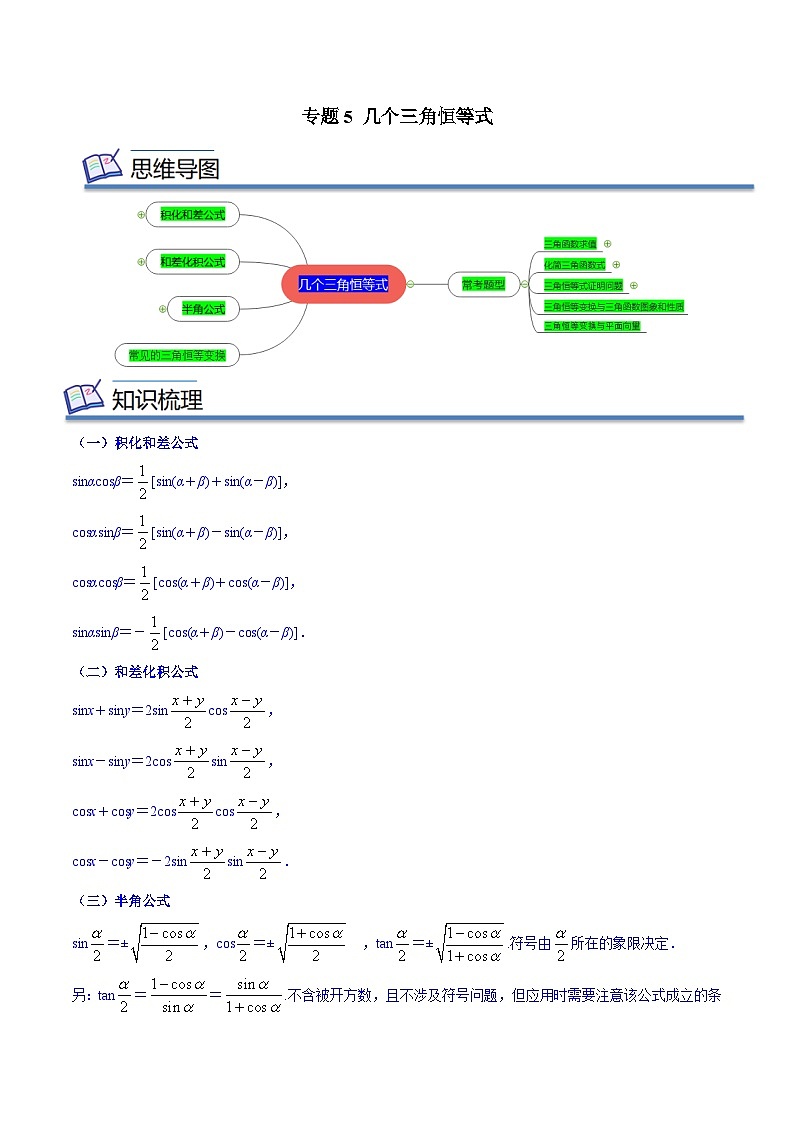
专题05 几个三角恒等式(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册)
展开sinαcsβ=[sin(α+β)+sin(α-β)],
csαsinβ=[sin(α+β)-sin(α-β)],
csαcsβ=[cs(α+β)+cs(α-β)],
sinαsinβ=-[cs(α+β)-cs(α-β)].
(二)和差化积公式
sinx+siny=2sincs,
sinx-siny=2cssin,
csx+csy=2cscs,
csx-csy=-2sinsin.
(三)半角公式
sin=±,cs=± ,tan=±.符号由所在的象限决定.
另:tan==.不含被开方数,且不涉及符号问题,但应用时需要注意该公式成立的条件.
(四)常见的三角恒等变换
(1)asinx+bcsx=sin(x+φ)(ab≠0),其中tanφ=,φ所在象限由a和b的符号确定.仅仅讨论=±1,±,±的情况.
(2)sin2x=,cs2x=,sinxcsx=sin2x.
(3)万能公式:设,则,,.可结合图中直角三角形的边角关系理解记忆.
题型一 三角函数求值
【典例1】(2023·江苏·高一专题练习)____.
【答案】## 0.5
【分析】根据和差化积公式和诱导公式可求出结果.
【详解】原式
.
故答案为:.
【典例2】(2023·江苏·高一专题练习) _____.
【答案】##
【分析】根据积化和差公式以及余弦的二倍角公式即可求解
【详解】
.
故答案为:
【典例3】(2022·高一课时练习)化简:___________.
【答案】
【分析】由诱导公式与三角恒变换公式求解即可
【详解】∵,
∴,
∴.
又∵,且,
∴
.
∵,
∴,
∴.
∴.
故答案为:
【典例4】(2022·高一课时练习)已知且,求:
(1);
(2).
【答案】(1)
(2)
【分析】先由同角的平方关系得到的值,从而得到,结合万能公式,分别代入(1)(2)中计算即可.
(1)因为,所以,于是.
设.
.
(2) .
【规律方法】
1.给角求值:一般不会给出特殊角!所以,应用各种公式,设法化成特殊角的函数值,或将待求值三角函数式,用已知表示出来.
2.给值求值:由给出的某些角的三角函数值,求另外一些角的三角函数值,关键在于“变角”使“目标角”变成“已知角”,另外角的范围应根据所给条件进一步缩小,避免出现增解.
3.已知的某个三角函数值,求的三角函数值的步骤是:(1)利用同角三角函数基本关系式求得的其他三角函数值;(2)代入半角公式计算即可.(3)应用半角公式求值时,要特别注意根据单角的范围去确定半角三角函数值的符号.
题型二 化简三角函数式
【典例5】(2022·高一课时练习)已知sin α+sin β=,cs α+cs β=,则tan(α+β)=________,cs(α-β)=________.
【答案】 ##
【分析】根据三角函数的和差化积把已知条件化简得到两个式子,然后把两式相除得到的正切值,再把所求的式子利用正切二倍角公式化简,代入即可求出值;对,,两式分别平方求和可得.
【详解】
,
即①,
,
即②,
①②两式相除得,
则;
,
,
两式相加可得,
.
故答案为:①;②.
【典例6】化简sin2α·sin2β+cs2α·cs2β-cs2αcs2β.
【答案】见解析
【解析】解法一:(从“角”入手,倍角化单角)
原式=sin2α·sin2β+cs2α·cs2β-(2cs2α-1)(2cs2β-1)
=sin2α·sin2β+cs2α·cs2β-(4cs2αcs2β-2cs2α-2cs2β+1)
=sin2α·sin2β-cs2α·cs2β+cs2α+cs2β-
=sin2α·sin2β+cs2α(1-cs2β)+cs2β-
=sin2α·sin2β+cs2αsin2β+cs2β-
=sin2β(sin2α+cs2α)+cs2β-
=sin2β+cs2β-=1-=.
解法二:(从“幂”入手,利用降幂公式先降次)
原式=·+·-cs2α·cs2β
=(1+cs2α·cs2β-cs2α-cs2β)+(1+cs2α·cs2β+cs2α+cs2β)-cs2α·cs2β=+=.
【典例7】(2023秋·陕西西安·高一校考期末)(1)化简:;
(2)求值:.
【答案】(1);(2)2
【分析】(1)化切为弦,结合正弦和余弦的倍角公式和半角公式得到答案;
(2)化切为弦,结合辅助角公式和诱导公式进行求解.
【详解】(1);
(2)
.
【典例8】(2022·高一课时练习)化简:
(1);
(2).
【答案】(1)
(2)
【分析】(1)先求出的范围,再利用二倍角公式和同角三角函数间的关系化简计算即可,
(2)利用半角公式,诱导公式和二倍角公式化简即可.
(1)
因为,所以,
所以原式
.
(2)
因为,
所以.
又因为,且,
所以原式,
因为,所以,所以.
所以原式.
【规律方法】
三角函数式的化简,主要有以下几类:(1)对三角的和式,基本思路是降幂、消项和逆用公式;(2)对三角的分式,基本思路是分子与分母的约分和逆用公式,最终变成整式或较简式子;(3)对二次根式,则需要运用倍角公式的变形形式.在具体过程中体现的则是化归的思想,是一个“化异为同”的过程,涉及切弦互化,即“函数名”的“化同”;角的变换,即“单角化倍角”“单角化复角”“复角化复角”等具体手段,以实现三角函数式的化简.
题型三 三角恒等式证明问题
【典例9】(2023·江苏·高一专题练习)已知.求证:.
【答案】证明见解析
【分析】由,结合万能公式化简可得结果.
【详解】.
【典例10】(2021春·上海·高一期中)求证:.
【答案】证明见解析.
【分析】法一:正切的半角公式有,代入左式化简,即可证明等式成立;法二:由,代入左式得,再由即可证等式成立.
【详解】(方法一)左边右边,所以原恒等式成立.
(方法二)左边右边,所以,原等式成立.
【典例11】(2023·江苏·高一专题练习)已知.求证:.
【答案】证明见解析
【分析】由,结合万能公式化简可得结果.
【详解】.
【典例12】(2022·高一课时练习)已知,求证:.
【答案】证明见解析
【分析】由已知条件化简得出,利用积化和差公式化简可证得结论成立.
【详解】证明:因为,所以,
于是,
因为
,
所以,,
同理可得,
所以,从而,所以.
【规律方法】
1.三角函数等式的证明包括无条件三角函数等式的证明和有条件三角函数等式的证明.对于无条件三角函数等式的证明,要认真分析等式两边三角函数式的特点,找出差异,化异角为同角,化异次为同次,化异名为同名,寻找证明的突破口.对于有条件三角函数等式的证明,要认真观察条件式与被证式的区别与联系,灵活使用条件等式,通过代入法、消元法等方法进行证明.
2. 三角恒等变换常见变形策略有:变角、变名、变次,其中变角是核心;常见变角形式有:2α=(α-β)+(α+β),=α+-(+β)等
题型四 三角恒等变换与三角函数图象和性质
【典例13】(2023·江苏·高一专题练习)已知函数.
(1)求的最小正周期及单调区间;
(2)求在区间上的最大值与最小值.
【答案】(1)最小正周期为,单调增区间为,单调减区间为.
(2)最大值为2,最小值为
【分析】(1)先利用三角恒等变换化简得到,从而利用求出最小正周期,再利用整体法求解函数的单调区间;
(2)根据求出,从而结合函数图象求出最大值为2,最小值为.
【详解】(1)因为
所以的最小正周期;
令,,解得:,,
令,,解得:,,
单调增区间为,,
单调减区间为,;
(2)已知,所以,
当,即时,取得最大值,最大值为2,
当,即时,取得最小值,最小值为-1,
所以在区间上的最大值为2,最小值为.
【典例14】(2021春·湖南·高一周南中学校联考开学考试)已知函数,.
(1)若是第三象限角,且,求的值;
(2)设,讨论在区间上的单调性.
【答案】(1)
(2)在上递增,在递减
【分析】(1)根据和差角公式展开即可得,进而,再根据同角三角函数关系得,最后结合半角公式求解即可;
(2)结合(1)得,再结合题意得,进而解和即可得单调区间.
(1)
解:
因为,所以
因为是第三象限角,所以,
.
(2)
解:由(1)得,
因为,所以
要使为增函数,则,解得
要使为减函数,则,解得
综上所述,当时,在上单调递增,在单调递减.
【规律方法】
当给出的三角函数关系式较为复杂,我们要先通过三角恒等变换,将三角函数的表达式变形化简,将函数表达式变形为y=Asin(ωx+φ)+k或y=Acs(ωx+φ)+k等形式,然后再根据化简后的三角函数,讨论其图象和性质.
题型五 三角恒等变换与平面向量
【典例15】(2021·全国·高考真题)已知为坐标原点,点,,,,则( )
A.B.
C.D.
【答案】AC
【分析】
A、B写出,、,的坐标,利用坐标公式求模,即可判断正误;C、D根据向量的坐标,应用向量数量积的坐标表示及两角和差公式化简,即可判断正误.
【详解】
A:,,所以,,故,正确;
B:,,所以,同理,故不一定相等,错误;
C:由题意得:,,正确;
D:由题意得:,
,故一般来说故错误;
故选:AC
【典例16】(2023·江苏·高一专题练习)已知向量,,设.
(1)求的值;
(2)求函数的最小正周期及单调递增区间.
【答案】(1)2
(2),单调递增区间为
【分析】(1)利用向量数量积的坐标表示结合二倍角和辅助角公式化简,再将代入即可求解;
(2)利用三角函数的性质即可求解.
【详解】(1)因为向量,,
所以
,
所以.
(2)由(1)得,
所以的最小正周期,
因为的单调递增区间为,
令,解得,
所以的单调递增区间为.
一、单选题
1.(2021春·江苏南京·高一南京市第一中学校考阶段练习)已知等腰三角形的顶角的余弦值等于,则它的底角的余弦值为( )
A.B.
C.D.
【答案】B
【分析】根据三角形内角和为,顶角为,则底角,再有诱导公式即可求解.
【详解】设等腰三角形的顶角为,底角为,则.又,
即,
故选B.
【点睛】本题考查三角诱导公式,需熟记公式.
2.(2023·江苏·高一专题练习)cs15° sin 105°=( )
A.+B.-
C.+1D.-1
【答案】A
【分析】利用积化和差公式直接求解.
【详解】.
故选:A.
3.(2023·江苏·高一专题练习)计算:( )
A.B.C.D.
【答案】D
【分析】利用和差化积公式可求解.
【详解】原式.
故选:D
4.(2021·江苏·高一假期作业)若,是第三象限的角,则( )
A.B.C.D.-2
【答案】D
【解析】根据,是第三象限的角,先利用半角公式求得,然后代入求解.
【详解】因为为第三象限角,
所以可能为二、四象限角,
所以,
所以.
故选:D.
5.(2021·高一课时练习)若,则( )
A.B.C.D.
【答案】C
【分析】利用半角公式,倍角公式,弦化切等进行化简求值.
【详解】
因为
所以分子分母同除以,可得:原式=
故选:C
6.(辽宁沈阳·高一东北育才学校校考阶段练习)函数的最小正周期为( )
A.πB.2πC.D.
【答案】B
【分析】首先进行三角函数的恒等变换,利用半角公式整理出只含有一倍角的形式,把乘到括号里,根据同角的三角函数之间的关系得到最简结果,利用周期公式计算即得周期.
【详解】函数
,
函数要有意义则必须有:,且,
即且
所以函数的定义域为:
且,
所以函数的最小正周期为,
故选:B.
7.(2022·高一课时练习)已知,且,则的值为( )
A.B.C.D.
【答案】B
【分析】由,结合已知及和差角余弦公式可得,进而可得,最后由倍角余弦公式求值.
【详解】因为,所以,
因为,所以,于是,
所以.
故选:B
8.(2022·高一课时练习)已知,为锐角,且,则的取值范围是( )
A.B.C.D.
【答案】A
【分析】由积化和差公式可得,根据角的范围即可根据三角函数的性质求解.
【详解】因为 ,又
所以.
∵,为锐角,且,∴,即,
∴,
∴,∴,
∴的取值范围为.
故选:A
二、多选题
9.(2022·高一课时练习)(多选)下列等式中错误的是( )
A.B.
C.D.
【答案】ABC
【分析】先证明和差化积公式,然后验证各选项.
【详解】因为,
,
从而有,,
对于A,;
对于B,;
对于C,;
对于D..
故选:ABC.
10.(2023秋·广东广州·高一广州市真光中学校考期末)下列各式中,值为的是( )
A.B.
C.D.
【答案】ABD
【分析】对于A,采用降幂公式,结合特殊角三角函数,可得答案;
对于B,根据特殊角三角函数,结合正切的和角公式,可得答案;
对于C,根据辅助角公式,结合特殊角三角函数,可得答案;
对于D,根据积化和差公式,结合特殊角三角函数,可得答案.
【详解】对于A,
,故A正确;
对于B,,故B正确;
对于C,
,故C错误;
对于D,
,故D正确;
故选:ABD.
三、填空题
11.(2023·江苏·高一专题练习)函数的最小正周期为________.
【答案】
【分析】化简得到,进而求出最小正周期.
【详解】,所以最小正周期为,
故答案为:
12.(2022春·上海徐汇·高一上海市徐汇中学校考阶段练习)已知,则__.
【答案】
【分析】根据半角公式或二倍角公式变形即可求解.
【详解】依题意,
.
故答案为:.
四、解答题
13.(2020·高一课时练习)求证:
(1).
(2).
【答案】(1)见解析 (2)见解析
【解析】(1)利用二倍角公式、同角三角函数关系化简整理即可证得结论;
(2)采用切化弦的方式,利用二倍角公式整理即可得到结果.
【详解】(1)左边
右边
故原式成立.
(2)左边右边
故原式成立.
14.(2023·江苏·高一专题练习)已知.
(1)若在第二象限,求的值;
(2)已知,且,求的值.
【答案】(1)
(2)
【分析】(1)根据题意,结合半角公式得,故,,再根据二倍角公式计算即可.
(2)由题知,再结合正切的和角公式求解即可.
【详解】(1)解: ,∴
∵在第二象限,∴,,
∴
(2)解:
∴,
15.(2022秋·江苏宿迁·高一泗阳县实验高级中学校考期末)已知函数.
(1)求函数在区间上的最大值和最小值;
(2)若,,求的值.
【答案】(1)最大值为2,最小值为.
(2)
【分析】(1)由二倍角公式、两角和的正弦展开式得,再利用正弦函数的单调性与范围可得答案;
(2)由得,利用平方关系得到,再利用展开可得答案.
【详解】(1)由得,因为,则,故当时,取最大值2;当时,取最小值;
所以函数在区间上的最大值为2,最小值为.
(2)由(1)可知,
又因为,所以,
由,得,
从而,
所以
.
16.(2023·江苏·高一专题练习)已知,,,
(1)求的值;
(2)求的值.
【答案】(1)
(2)
【分析】(1)根据同角三角函数的平方关系及诱导公式,再利用角凑配
及两角差的余弦公式即可求解;
(2)根据已知条件及二倍角公式,再结合半角公式即可求解.
【详解】(1)∵,∴,
∴,
, ,
∴,
∵
∴
∴
(2)由得
∴①
将①式两边平方得∴②
∵
∴
③
由①和③得
.
专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册): 这是一份专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册),文件包含专题03两角和与差的三角函数知识串讲+热考题型+专题训练原卷版docx、专题03两角和与差的三角函数知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
专题02 向量基本定理与坐标运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册): 这是一份专题02 向量基本定理与坐标运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册),文件包含专题02向量基本定理与坐标运算知识串讲+热考题型+专题训练原卷版docx、专题02向量基本定理与坐标运算知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
专题01 向量的概念与运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册): 这是一份专题01 向量的概念与运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册),文件包含专题01向量的概念与运算知识串讲+热考题型+专题训练原卷版docx、专题01向量的概念与运算知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。












