




- 专题02 向量基本定理与坐标运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题04 二倍角的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题05 几个三角恒等式(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
- 专题06 正弦定理、余弦定理及其应用(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册) 试卷 1 次下载
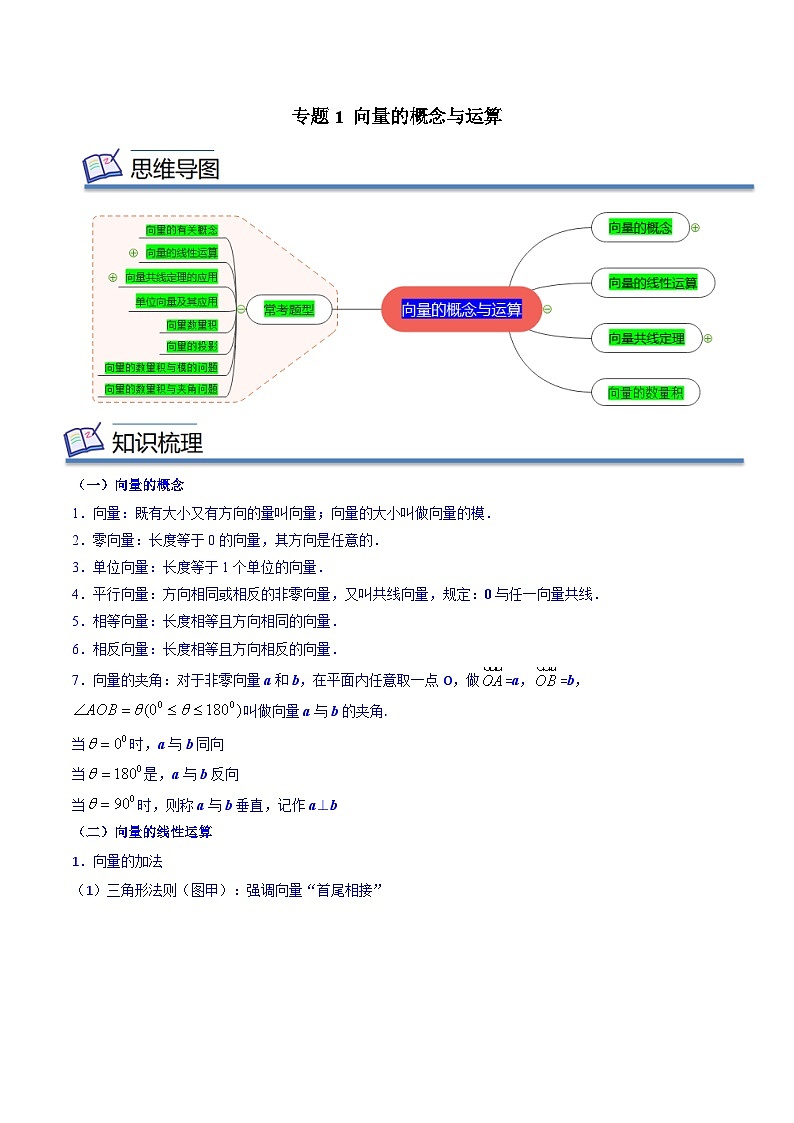
专题01 向量的概念与运算(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册)
展开(一)平面向量的概念
1.向量:既有大小又有方向的量叫向量;向量的大小叫做向量的模.
2.零向量:长度等于0的向量,其方向是任意的.
3.单位向量:长度等于1个单位的向量.
4.平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0与任一向量共线.
5.相等向量:长度相等且方向相同的向量.
6.相反向量:长度相等且方向相反的向量.
7.向量的夹角:对于非零向量a和b,在平面内任意取一点O,做=a,=b,叫做向量a与b的夹角.
当时,a与b同向
当是,a与b反向
当时,则称a与b垂直,记作a⊥b
(二)向量的线性运算
1.向量的加法
(1)三角形法则(图甲):强调向量“首尾相接”
(2)平行四边形法则(图乙):强调“共起点”
(3)向量加法的运算律
= 1 \* GB3 ①交换律
= 2 \* GB3 ②结合律
【点拨】 = 1 \* GB3 ①已知n个向量,依次首尾相接,则由起始向量的起点指向末尾向量的终点的向量即为这n个向量的和,这称为向量求和的多边形法则.
= 2 \* GB3 ②首尾顺次相接的若干向量求和,若构成一个封闭图形,则它们的和为0.
2. 向量减法
【点拨】 = 1 \* GB3 ①向量减法的三角形法则中,eq \(BA,\s\up6(→))表示a-b,强调了差向量的“箭头”指向被减向量.即作非零向量a,b的差向量a-b,可以简记为“共起点,连终点指向被减”.
= 2 \* GB3 ②如图,以AB,AD为邻边作平行四边形ABCD,则两条对角线所对应的向量eq \(AC,\s\up6(→))=a+b,eq \(DB,\s\up6(→))=a-b.
3. 向量的数乘
(1)
(2)几何意义:λa的几何意义就是把向量a沿着a的方向或反方向扩大或缩小|λ|倍.
(3)运算律
设λ、μ为实数,则
(1)λ(μa)= (λμ)a;
(2)(λ+μ)a=λa+μa;
(3)λ(a+b)=λa+λb (分配律).
特别地,我们有(-λ)a=-(λa)=λ(-a),λ(a-b)=λa-λb.
【点拨】对于非零向量a,当λ=eq \f(1,|a|)时,λa表示a方向上的单位向量.
4. 向量的线性运算
向量的加、减、数乘运算统称为向量的线性运算,对于任意向量a、b以及任意实数λ、μ1、μ2,恒有λ(μ1a±μ2b)=λμ1a±λμ2b.
(三)向量共线定理
1. 向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使得b=λa.
【点拨】 = 1 \* GB3 ①定理中a≠0不能漏掉.若a=b=0,则实数λ可以是任意实数;若a=0,b≠0,则不存在实数λ,使得b=λa.
= 2 \* GB3 ②定理的另种形式:若存在不全为0的一对实数t,s,使ta+sb=0,则a与b共线;若两个非零向量a与b不共线,且ta+sb=0,则必有t=s=0.
2.平面向量共线定理的三个应用
(四)向量的数量积
1.平面向量的数量积
2.两个向量数量积的性质
设a、b都是非零向量,
(1)a⊥b⇔a·b=0.
(2)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.特别地,a·a=a2=|a|2或|a|=eq \r(a·a).
(3)|a·b|≤|a||b|.
3.平面向量数量积的运算律
已知向量a、b、c和实数λ.
(1)交换律:a·b=b·a.
(2)结合律:(λa)·b=λ(a·b)=a·(λb).
(3)分配律:(a+b)·c=a·c+b·c.
题型一 向量的有关概念
【典例1】(2022·高一课时练习)下列命题中正确的个数是( )
①若向量与是共线向量,则A、B、C、D必在同一直线上;
②若向量与向量平行,则,方向相同或相反;
③若非零向量与是共线向量,则它们的夹角是0°或180°;
④若,则,是相等向量或相反向量.
A.0B.1C.2D.3
【答案】B
【分析】对于①,根据共线向量的定义,由向量为自由向量,可得答案;
对于②,由零向量的定义和性质,可得答案;
对于③,根据向量的数量积的性质,可得答案;
对于④,根据模长的定义,可知方向不确定,可得答案.
【详解】①错误,平行向量又叫共线向量,向量与是共线向量,则与平行或共线;
②错误,与至少有一个为零向量时,结论不成立;由向量的夹角可知③正确;
④错误,由,只能说明,的长度相等,确定不了方向.
故选:B.
【典例2】【多选题】(2022·高一单元测试)下列说法中正确的是( )
A.若为单位向量,则B.若与共线,则或
C.若,则D.是与非零向量共线的单位向量
【答案】CD
【分析】根据向量的基本概念,以及零向量和单位向量的定义,逐项判定,即可求解.
【详解】对于A中,向量的方向不一定相同,所以A错误;
对于B中,向量与的长度不一定相等,所以B错误;
对于C中,由,根据零向量的定义,可得,所以C正确;
对于D中,由,可得与向量同向,
又由的模等于,所以是与非零向量共线的单位向量,所以D正确.
故选:CD.
【易错提醒】
有关平面向量概念的注意点
(1)相等向量具有传递性,非零向量的平行也具有传递性.
(2)共线向量即为平行向量,它们均与起点无关.
(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混淆.
(4)两个向量不能比较大小,只可以判断它们是否相等,但它们的模可以比较大小.
(5)两平行向量有向线段所在的直线平行或重合,易忽视重合这一条件.
题型二 向量的线性运算
【典例3】(2021春·江苏镇江·高一校考阶段练习)如图所示,在中,点是线段上靠近A的三等分点,点是线段的中点, 则( )
A. B.
C. D.
【答案】B
【分析】由向量线性运算的几何意义即可计算
【详解】.
故选:B
【典例4】(2023·高一单元测试)已知,若记,则______.
【答案】
【分析】由向量的线性运算,求解的值.
【详解】,
∴,
则有,
∴.
故答案为:
【规律方法】
1.关于向量的线性运算的考查,命题角度主要有两个:一是向量的线性运算,二是利用向量线性运算求参数.解题过程中应注意:
①常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连向量的和用三角形法则.
②找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.
2.向量的线性运算技巧
(1)不含图形的情况:可直接运用相应运算法则求解.
(2)含图形的情况:将它们转化到三角形或平行四边形中,充分利用相等向量、相反向量、三角形的中位线等性质,把未知向量用已知向量表示出来求解.
3.利用向量的线性运算求参数的一般思路
(1)没有图形的准确作出图形,确定每一个点的位置.
(2)利用平行四边形法则或三角形法则进行转化,转化为要求的向量形式.
(3)比较、观察可知所求.
题型三 向量共线定理及其应用
【典例5】(2023秋·北京房山·高一统考期末)已知向量,不共线,且,,.
(1)将用,表示;
(2)若,求的值;
(3)若,求证:A,B,C三点共线.
【答案】(1);
(2);
(3)详见解析.
【分析】(1)根据向量的减法运算即得;
(2)根据向量共线定理可得,进而可得,即得;
(3)由题可得,然后根据向量共线定理结合条件即得.
【详解】(1)因为,,
所以;
(2)因为,,,
所以,即,又向量,不共线,
所以,解得,
即的值为;
(3)当时, ,,,
所以,
所以,又有公共点,
所以A,B,C三点共线.
【典例6】(2023·全国·高一专题练习)设是不共线的两个向量.
(1)若,求证:三点共线;
(2)若与共线,求实数的值.
【答案】(1)证明见解析
(2).
【分析】(1)要证明三点共线,即证明三点组成的两个向量共线即可.
(2)由共线性质求出参数即可.
【详解】(1)证明:因为,
而
所以,
所以与共线,且有公共点,
所以三点共线
(2)因为与共线
所以存在实数,使得,
因为与不共线,
所以,
解得,.
【规律方法】
求解向量共线问题的注意事项
(1)向量共线的充要条件中,当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,注意待定系数法和方程思想的运用.
(2)证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线.
题型四 单位向量的应用
【典例7】(2022春·浙江丽水·高一统考期末)若为非零向量,则“”是“共线”的( )
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
【答案】B
【分析】表示与同向的单位向量,共线可能同向共线、也可能反向共线,再由充分性、必要性的定义可求出答案.
【详解】依题意为非零向量, 表示与同向的单位向量,表示与同向的单位向量,
则表示与同向的单位向量,所以能推出共线,所以充分性成立;
共线可能同向共线、也可能反向共线,所以共线得不出,所以必要性不成立.
故选:B.
【典例8】(2023·高一课时练习)已知O为平面上一定点,A、B、C是平面上不共线的三个点,动点D满足:,则点D一定在的______线所在直线上.
【答案】角A的平分
【分析】根据分别表示平行于的单位向量,平分求解.
【详解】解:因为,
所以,
而分别表示平行于的单位向量,
所以平分,即平分,
所以点D一定在的角A的平分线所在直线上,
故答案为:角A的平分
【规律方法】
非零向量a与eq \f(a,|a|)的关系:eq \f(a,|a|)是与a同方向的单位向量,-eq \f(a,|a|)是与a反方向的单位向量.
题型五 向量的数量积
【典例9】(2023·高一单元测试)在中,分别为的中点,则__________.
【答案】-4
【分析】由向量的线性运算得,,然后计算数量积可得.
【详解】由已知,,
.
故答案为:.
【典例10】(2022春·重庆北碚·高一西南大学附中校考阶段练习)如图,A,B是单位圆上的相异两定点(为圆心),(为锐角),点C为单位圆上的动点,线段AC交线段于点M(点M异于点、B)
(1)求(结果用表示);
(2)若
①求的取值范围;
②设,记,求的最小值.
【答案】(1)
(2)①;②
【分析】(1)由,再结合平面向量的数量积,得解;
(2)①设,,化简可得,再根据正弦函数的图象与性质,得解;
②设,由,结合,推出,再利用分离常数法和基本不等式,得解.
【详解】(1)解:;
(2)解:①设,,
则,
,,
又,则.
②设,则,
因为,
所以,
所以,
因为,所以,即,
化简得,,
所以,
当且仅当,即时,等号成立,
故的最小值为.
【总结提升】
求向量的数量积的两个关键点
(1)求向量的数量积时,需明确两个关键点:相关向量的模和夹角.
(2)若相关向量是两个或两个以上向量的线性运算,则需先利用向量数量积的运算律及多项式乘法的相关公式进行化简.
题型六 向量的投影
【典例11】(2023·全国·高一专题练习)已知,求在上的投影向量.
【答案】
【分析】利用投影向量公式与向量的数量积运算法则即可得解.
【详解】因为,,
所以,
所以在上的投影向量为.
【规律方法】
求一个向量在另一个向量方向上的投影向量时,首先要根据题意确定向量的模及两向量的夹角,然后代入公式计算即可.
题型七 向量的数量积与模的问题
【典例12】(2023春·安徽淮北·高一淮北师范大学附属实验中学校考阶段练习)如图,在菱形ABCD中,,,则______.
【答案】
【分析】根据向量加法运算结合菱形的性质及角度,求出模长即可
【详解】如图所示,设菱形对角线交点为O,.
因为,所以,
所以为等边三角形.
又,,
所以.
在中,,
所以.
故答案为:
【典例13】(2022春·河南信阳·高一信阳高中校考阶段练习)已知为平面内任意两个非零向量,且他们夹角等于,若存在使得,则实数m的取值范围为___________.
【答案】
【分析】由平面向量数量积的运算结合已知得出,参变分离根据二次函数值域得到,通过题意得出,即可得出答案.
【详解】为平面内任意两个非零向量,且他们夹角等于,
,
,
则,
,
,
,
,
,,
,
,
故答案为:.
【总结提升】
利用数量积求解长度(模)问题是数量积的重要应用,此类问题的处理方法是:
(1)a=a·a=|a|2或|a|=eq \r(a·a).
(2) .
题型八 向量的数量积与夹角问题
【典例14】(2023春·安徽合肥·高一合肥一中校考阶段练习)已知,均为单位向量,,则与的夹角为( )
A.30°B.45°C.135°D.150°
【答案】A
【分析】根据,求得,再利用向量夹角公式即可求解.
【详解】因为,
所以.
设与的夹角为θ,则
又因为0°≤θ≤180°,所以θ=30°.
故选:A.
【典例15】(2023春·安徽安庆·高一安庆一中校考阶段练习)已知,,.
(1)求的值;
(2)求向量与夹角的余弦值.
【答案】(1)
(2)
【分析】(1)直接展开,代入即可求解;
(2)先分别求出,再直接代入向量夹角公式即可求解.
【详解】(1)依题意,
因为,
所以,
因为|,所以,
所以.
(2)因为,
,
所以.
令与的夹角为θ,
则,
所以向量与夹角的余弦值是.
【总结提升】
1.应用向量夹角公式cs〈a,b〉=eq \f(a·b,|a||b|),要注意涉及到了向量运算和数量运算.
2. 注意应用a⊥b⇔a·b=0.
一、单选题
1.(2023春·安徽合肥·高一合肥一中校考阶段练习)在如图所示的半圆中,AB为直径,点O为圆心,C为半圆上一点,且,,则等于( )
A.1B.C.D.2
【答案】A
【分析】根据,可得,进一步得出答案.
【详解】如图,连接AC,
由,得.
因为为半圆上的点,所以,
所以.
故选:A.
2.(2023春·安徽合肥·高一合肥一中校考阶段练习)下列五个结论:
①温度有零上和零下之分,所以温度是向量;
②向量,则与的方向必不相同;
③,则;
④向量是单位向量,向量也是单位向量,则向量与向量共线;
⑤方向为北偏西的向量与方向为东偏南的向量一定是平行向量.
其中正确的有( )
A.①⑤B.④C.⑤D.②④
【答案】C
【分析】根据向量的定义即可判断①;根据不相等向量的定义即可判断②;根据向量不能比较大小即可判断③;根据共线向量的定义即可判断④⑤.
【详解】温度虽有大小却无方向,故不是向量,故①错;
,但与的方向可以相同,故②错;
向量的长度可以比较大小,但向量不能比较大小,故③错;
单位向量只要求长度等于1个单位长度,但方向未确定,故④错;
如图,作出这两个向量,
则方向为北偏西的向量与方向为东偏南的向量方向相反,
所以这两个向量一定是平行向量,故⑤正确.
故选:C.
3.(2023·全国·高一专题练习)如图,在中,是的中点,若,,则等于( )
A. B.
C.D.
【答案】D
【分析】利用三角形法则与平行四边形法则表示向量.
【详解】因为是的中点,,,
所以,
所以.
故选:D.
4.(2022春·上海宝山·高一上海市行知中学校考阶段练习)设是非零向量,分别是的单位向量,则下列各式中正确的是( )
A.B.或
C.D.
【答案】D
【分析】根据相等向量的定义,结合单位向量的定义逐一判断即可.
【详解】两个向量模相等,但是方向也可能不同,所以选项AB不正确;
题中没有明确向量模的大小关系,所以选项C不正确;
因为分别是的单位向量,所以,
故选:D
5.(2023·全国·高一专题练习)若,|,的夹角为,则等于( ).
A.B.
C.D.
【答案】B
【分析】根据向量数量积的定义计算即可.
【详解】因为,的夹角为,
所以.
故选:B.
6.(2023秋·江苏无锡·高一无锡市第一中学校考期末)若非零向量、满足,且,则向量、的夹角为( )
A.B.C.D.
【答案】B
【分析】设向量、的夹角为,由已知可得出,根据平面向量数量积的运算性质求出的值,结合角的取值范围可得出角的值.
【详解】设向量、的夹角为,由题意,,
又因为,因此,.
故选:B.
7.(2023春·安徽安庆·高一安庆一中校考阶段练习)已知是单位向量,,若向量满足,则的取值范围是( )
A.[-1,+1]B.[-1,+2]
C.[1,+1]D.[1,+2]
【答案】A
【分析】将两边同时平方,转化为关于的一元二次不等式即可求解.
【详解】∵是单位向量,∴.
∵
且.
∴,又∵,
∴ (θ是与的夹角).
又-1≤csθ≤1,
∴,
∴.
根据一元二次不等式的解法,
解得.
故选:A.
8.(2023秋·云南·高一云南师大附中校考期末)在正三角形△ABC中,,M,N分别为AB,AC的中点,则( )
A.B.C.D.
【答案】A
【分析】由题可知,向量,的夹角为150°,再由平面向量数量积的定义即可得出答案.
【详解】由题知,,,向量,的夹角为150°,
所以.
故选:A.
二、多选题
9.(2023·全国·高一专题练习)下列说法正确的是( )
A.向量在向量上的投影向量可表示为
B.若,则与的夹角θ的范围是
C.若是等边三角形,则,的夹角为
D.若,则
【答案】AB
【分析】根据投影向量的定义即可判断A;根据数量积的计算公式即可判断B;根据向量夹角的定义即可判断C,根据数量积的计算公式即可判断D.
【详解】对于选项A,根据投影向量的定义可得向量在向量上的投影向量为,故A正确;
对于选项B,因为,所以,
又,所以,故B正确;
对于选项C,若是等边三角形,则,的夹角为,故C错误;
对于选项D,因为,所以或或,故D错误.
故选:AB.
10.(2023秋·云南·高一云南师大附中校考期末)设,是互相垂直的单位向量,,,下列选项正确的是( )
A.若点C在线段AB上,则
B.若,则
C.当时,与共线的单位向量是
D.当时,在上的投影向量为
【答案】ABD
【分析】对A:根据向量共线分析运算;对B:根据向量垂直运算求解;对C:根据单位向量分析运算;对D:根据投影向量分析运算.
【详解】由题意可得:,
对A:若点C在线段AB上,则,则,
可得,解得或(舍去),故A正确;
对B:由,可得,
解得,故B正确;
对C:当时,则,
与共线的单位向量是,故C错误;
对D:当时,可得,
则在上的投影向量为,故D正确.
故选:ABD.
三、填空题
11.(2023·江苏·高一专题练习)已知A、B、C是不共线的三点,向量与向量是平行向量,与是共线向量,则=________.
【答案】
【分析】依据向量共线的定义及零向量定义即可求得向量.
【详解】向量与向量是平行向量,则向量与向量方向相同或相反;
向量与是共线向量,则向量与向量方向相同或相反,
又由A、B、C是不共线的三点,可知向量与向量方向不同且不共线
则=.
故答案为:
12.(2023·高一课时练习)已知,与的夹角为,是与同向的单位向量,则在方向上的投影向量为______.
【答案】
【分析】根据则在方向上的投影向量的定义可得
【详解】在方向上的投影向量为,
故答案为:.
四、解答题
13.(2021秋·新疆喀什·高一校考期末)如图,在中,,,点是的中点,点在上,且,求证:、、三点共线.
【答案】证明见解析
【分析】用、为一组基底表示出、,即可得到,从而得证.
【详解】证明:设,,
由已知点是的中点,点在上,且,
,
,
、、三点共线.
14.(2022春·河南三门峡·高一校考阶段练习)已知,求分别在下列条件下的值.
(1);
(2);
(3).
【答案】(1);
(2);
(3).
【分析】(1)根据平面向量数量积的定义进行求解即可;
(2)根据互相垂直的两个向量数量积的性质进行求解即可;
(3)根据平面向量数量积的定义,结合共线向量的性质进行求解
【详解】(1)
(2)因为,所以.
(3)因为,所以与的夹角为或,
所以.
15.(2023春·河南新乡·高一校考开学考试)已知,,且与夹角为,求:
(1);
(2)与的夹角.
【答案】(1);
(2).
【分析】(1)根据数量积的运算律,求出的值,即可得出答案;
(2)先根据数量积的运算律,求出的值,即可得出的值,进而根据数量积的运算得出的值.然后根据夹角公式,即可得出结果.
【详解】(1)由已知可得,.
所以有,
所以.
(2)因为,
所以.
又,
所以,
所以与的夹角为.
16.(2021春·四川成都·高一统考期中)已知向量,满足:,,且.
(1)求向量与的夹角.
(2)求的值.
【答案】(1)
(2)
【分析】(1)向量与的夹角为,,直接利用数量积的运算律及数量积的定义可得夹角;
(2)利用,利用数量积的运算律展开,然后代入向量的模和数量积计算即可.
【详解】(1)设向量与的夹角为,,
,
解得,
,即向量与的夹角为;
(2)由(1)得,
.
定义
一般地,实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λa
长度
|λa|=|λ||a|
方向
λ>0
λa的方向与a的方向相同
λ=0
λa=0(零向量!)
λ<0
λa的方向与a的方向相反
定义
已知两个非零向量a与b,我们把数量|a||b|csθ叫做a与b的数量积(或内积),其中θ是a与b的夹角
记法
记作a·b,即a·b=|a||b|csθ
规定
零向量与任一向量的数量积为0
投影向量
(|a|csθ ) ((|b|csθ) )叫做向量a在b上(b在a上)的投影向量
几何意义
数量积a·b等于a的长度|a|与b在a的方向上的投影向量的乘积
专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册): 这是一份专题03 两角和与差的三角函数(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末常考考点精讲精练(苏教版必修第二册),文件包含专题03两角和与差的三角函数知识串讲+热考题型+专题训练原卷版docx、专题03两角和与差的三角函数知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
专题13 概率综合(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末考点大串讲(人教A版2019必修第二册): 这是一份专题13 概率综合(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末考点大串讲(人教A版2019必修第二册),文件包含专题13概率综合原卷版docx、专题13概率综合解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
专题12 统计综合(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末考点大串讲(人教A版2019必修第二册): 这是一份专题12 统计综合(知识串讲+热考题型+专题训练)-2023-2024学年高一数学下学期期中期末考点大串讲(人教A版2019必修第二册),文件包含专题12统计综合原卷版docx、专题12统计综合解析版docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。













