2024八年级数学下册第19章平面直角坐标系19.4坐标与图形的变化2用坐标表示图形的对称放缩习题课件新版冀教版

这是一份2024八年级数学下册第19章平面直角坐标系19.4坐标与图形的变化2用坐标表示图形的对称放缩习题课件新版冀教版，共23页。

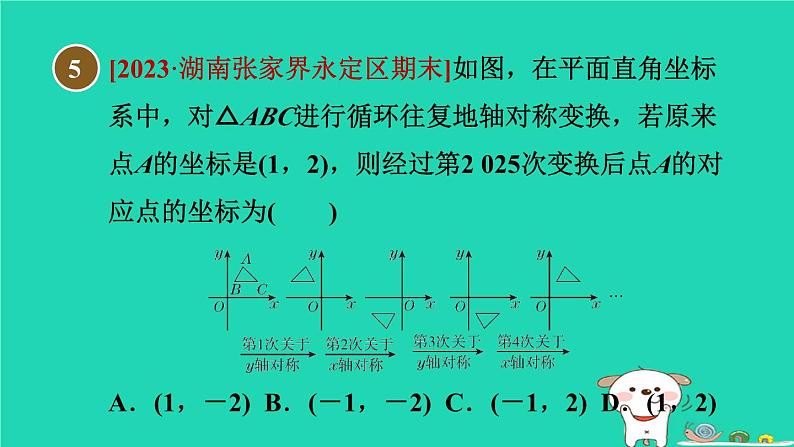
冀教版 八年级下第十九章 平面直角坐标系用坐标表示图形的对称、放缩19.4.2[2023·怀化]在平面直角坐标系中，点P(2，－3)关于x轴对称的点P′的坐标是(　　)A．(－2，－3) B．(－2，3)C．(2，－3) D．(2，3)1D[2023·衡水五中期中]已知两点的坐标分别是(－2，3)和(2，3)，给出下列说法：①两点关于x轴对称；②两点关于y轴对称；③两点之间的距离为4.其中正确的是________．(填序号)②③2[2023·临沂]某小区的圆形花园中间有两条互相垂直的小路，园丁在花园中栽种了8棵桂花，如图所示．若A，B两处桂花的位置关于小路对称，在分别以两条小路为x轴，y轴的平面直角坐标系内，若点A的坐标为(－6，2)，则点B的坐标为(　　)A．(6，2) B．(－6，－2)C．(2，6) D．(2，－6)3A[2023·聊城]如图，在直角坐标系中，△ABC各顶点的坐标分别为A(－2，1)，B(－1，3)，C(－4，4)，先作△ABC关于x轴成轴对称的△A1B1C1，再把△A1B1C1平移后得到△A2B2C2.若B2(2，1)，则点A2的坐标为(　　)A．(1，5) B．(1，3)C．(5，3) D．(5，5)4【点拨】【答案】B由题意得A(－2，1)，B(－1，3)关于x轴对称的点的坐标为A1(－2，－1)，B1(－1，－3)．∵B2(2，1)，∴平移规律为向右平移3个单位长度，向上平移4个单位长度．∴点A2的坐标为(－2＋3，－1＋4)，即(1，3)．故选B.[2023·湖南张家界永定区期末]如图，在平面直角坐标系中，对△ABC进行循环往复地轴对称变换，若原来点A的坐标是(1，2)，则经过第2 025次变换后点A的对应点的坐标为(　　)A．(1，－2) B．(－1，－2) C．(－1，2) D．(1，2)5【点拨】【答案】C点A第1次关于y轴对称后在第二象限，点A第2次关于x轴对称后在第三象限，点A第3次关于y轴对称后在第四象限，点A第4次关于x轴对称后在第一象限，即点A回到原始位置，∴每4次对称为一个循环．∵2 025÷4＝506……1，∴经过第2 025次变换后点A的对应点与第1次变换后的位置相同，在第二象限，坐标为(－1，2)．故选C.6A如图，将△ABC的三个顶点的纵坐标都乘－1，横坐标保持不变，则所得图形与原图形的位置关系是(　　)A．关于x轴对称B．关于y轴对称C．关于原点对称D．将原图形向左平移了1个单位长度7A如图，在平面直角坐标系中，将△ABO进行两次变换，第一次是各边扩大到原来的2倍，第二次是画出扩大后的图形关于原点对称的图形，得到△A′B′O.若点A的坐标是(1，2)，则点A′的坐标是(　　)A．(2，4)B．(－1，－2)C．(－2，－4)D．(－2，－1)8【点拨】【答案】C将△ABO的各边扩大到原来的2倍，即△ABO各点的横、纵坐标应分别乘2，根据题意，再将得到的点的横、纵坐标都乘－1，从而可得点A′的坐标是(－2，－4)．△ABC经过两次轴对称(x轴和y轴为对称轴)变化后，得到△DEF，如果A，B，C各点的坐标分别为A(－5，1)，B(－2，0)，C(1，3)，那么点A，B，C的对应点D，E，F的坐标分别为D________，E________，F____________.9(5，－1)(2，0)(－1，－3)已知，△OA1A2，△A3A4A5，△A6A7A8，…都是边长为2的等边三角形，按如图所示摆放，点A2，A3，A5，…都在x轴正半轴上，且A2A3＝A5A6＝A8A9＝…＝1，则点A2 023的坐标是____________．【点拨】如图，正方形ABCD四个顶点的坐标分别是A(1，1)，B(1，－1)，C(－1，－1)，D(－1，1)．求将正方形ABCD各顶点的横、纵坐标都乘2后得到的正方形的面积.解：新正方形是将原正方形放大为原来的2倍得到的，故新正方形的面积等于原正方形面积的2倍，所以新正方形的面积＝2×(2×2)＝8.上面的解答正确吗？如果不正确，请你写出正确的解答过程．【解】不正确．设将正方形ABCD各顶点的横、纵坐标都乘2后得到正方形A′B′C′D′，则A′(2，2)，B′(2，－2)，C′(－2，－2)，D′(－2，2)，∴正方形A′B′C′D′的边长为4，∴新正方形的面积为4×4＝16.如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3.相关顶点坐标分别为A(1，3)，A1(2，3)，A2(4，3)，A3(8，3)，B(2，0)，B1(4，0)，B2(8，0)，B3(16，0)．(1)观察每次变换前后的三角形的变化，找出规律，按此变换规律再将△OA3B3变换成△OA4B4，则点A4的坐标为________，点B4的坐标为________；(2)若按(1)中找出的规律，将△OAB进行n(n为正整数)次变换后，得到△OAnBn，直接写出点An，Bn的坐标．(16，3)(32，0)【解】An(2n，3)，Bn(2n＋1，0)．有下列问题：如图，在平面直角坐标系中的一系列格点Ai(xi，yi)，其中i＝1，2，3，…，n，…，且xi，yi是整数.记an＝xn＋yn.如A1(0，0)，即a1＝0，A2(1，0)，即a2＝1，A3(1，－1)，即a3＝0，…，以此类推，则下列结论正确的是(　　)A．a2 023＝40 B．a2 024＝43C．a(2n－1)2＝2n－6 D．a(2n－1)2＝2n－4B