






适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练16函数图象课件新人教A版
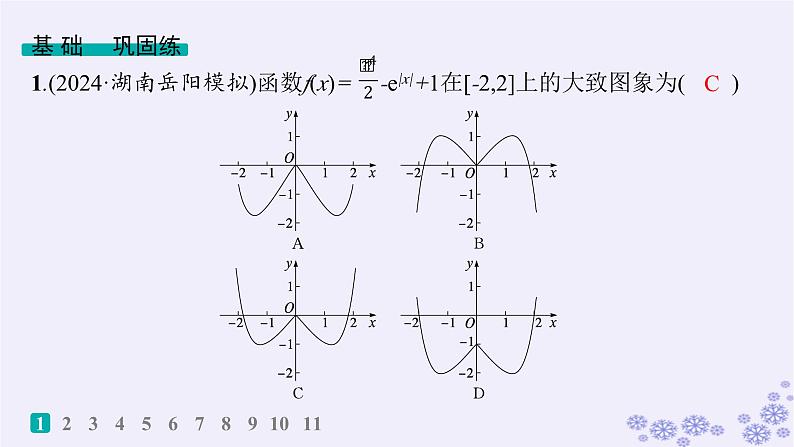
展开1.(2024·湖南岳阳模拟)函数f(x)= -e|x|+1在[-2,2]上的大致图象为( )
2. (2024·陕西西安模拟)已知函数f(x)在区间[-2,2]上的大致图象如图所示,则f(x)的解析式可以是( )A.f(x)=(ex-e-x)xB.f(x)=(ex-e-x)sin xC.f(x)=(ex-e-x)cs xD.f(x)=(ex-e-x)x2
解析 容易判断选项A,B中的函数都是偶函数,图象应关于y轴对称,与已知图象不符,选项C,D中的函数都是奇函数,图象关于原点对称,对于选项D,当x>0时,ex>1,e-x= <1,可得ex-e-x=ex- >0,因此f(x)=(ex-e-x)x2>0,图象应在x轴上方,与已知图象不符,故选C.
3.(2024·山东济南模拟)已知函数f(x)= 若f(m)>f(-m),则实数m的取值范围是( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(0,1)D.(-∞,-1)∪(0,1)
解析 画出函数的图象(如图所示),可知函数为奇函数,所以不等式f(m)>f(-m)等价于f(m)>-f(m),即f(m)>0,观察函数图象可得实数m的取值范围是(-1,0)∪(1,+∞),故选A.
5.(多选题)(2024·山西大同模拟)已知函数f(x)= 则下列判断错误的是( )A.f(x)是奇函数B.f(x)的图象与直线y=1有两个交点C.f(x)的值域是[0,+∞)D.f(x)在区间(-∞,0)上单调递增
解析 作出函数图象(如图所示),显然图象不关于原点中心对称,故A错误;f(x)图象与直线y=1有一个交点,故B错误;由图象知函数的值域为[0,+∞),且在区间(-∞,0)内单调递增,故C,D正确.故选AB.
6.(2024·上海杨浦模拟)已知函数f(x)=lg x+x2-1,则不等式f(x)>0的解集是 .
解析 不等式f(x)>0,即lg x+x2-1>0,所以lg x>1-x2.在同一坐标系中作出函数y=lg x,y=-x2+1的图象(如图所示),由图可知,满足不等式lg x>-x2+1的x的取值范围为(1,+∞),所以不等式f(x)>0的解集是(1,+∞).
7. (2024·湖南郴州模拟)若函数f(x)= 的图象如右图所示,则ab 0(填“>”或“<”)
8.(2024·山东潍坊模拟)设0
2)<0,解得0
A.0个B.1个C.2个D.3个
解析 根据“共生点对”的概念知,作出函数y= ,x>0的图象关于原点对称的图象与函数y=2x2+4x+1(x≤0)的图象(如图所示),由图可知它们的交点有两个,所以函数y的“共生点对”有2个,故选C.
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练18函数模型及其应用课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练18函数模型及其应用课件新人教A版,共22页。
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练15对数函数课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练15对数函数课件新人教A版,共20页。PPT课件主要包含了fxlnx,4+∞等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练14指数函数课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练14指数函数课件新人教A版,共21页。PPT课件主要包含了ABD,x+1,ABC等内容,欢迎下载使用。












