






适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量素能培优九球与几何体的切接问题课件新人教A版
展开球的切、接问题是历年高考的热点内容,经常以客观题形式出现.一般围绕球与其他几何体的内切、外接命题,考查球的体积与表面积,其关键点是确定球心.
考点一 外接球(多考向探究预测)
考向1定义法例1(2022·新高考Ⅱ,7)已知正三棱台的高为1,上、下底面的边长分别为 ,其顶点都在同一球面上,则该球的表面积为( )A.100πB.128πC.144πD.192π
解析 设外接球的半径为R,由题意得,上底面所在平面截球所得圆的半径是3,下底面所在平面截球所得圆的半径是4,在轴截面中,设球心到上、下底
解析 如图,在正三棱锥S-ABC中,△ABC是正三角形,点M是△ABC的中心,则此正三棱锥外接球的球心位于高SM所在的直线上,设为点O,设球的半径
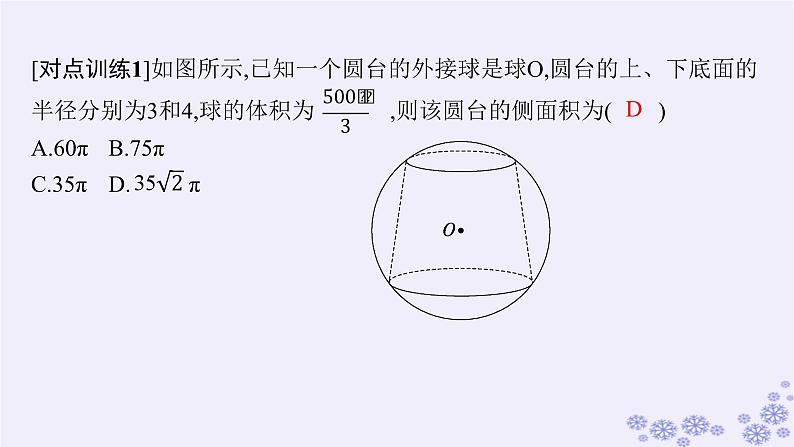
[对点训练1]如图所示,已知一个圆台的外接球是球O,圆台的上、下底面的半径分别为3和4,球的体积为 ,则该圆台的侧面积为( )A.60πB.75πC.35πD. π
解析 设球的半径为R,则 ,所以R=5.作圆台的轴截面ABCD,如图所示.设圆台的上、下底面圆心分别为F,E,则E,F分别为AB,CD的中点.连接OE,OF,OA,OB,OC,OD,则OA=OB=OC=OD=5,所以OE⊥AB,OF⊥CD,所以
因为OE=DF,OA=DO,AE=OF,所以Rt△OAE≌Rt△DOF,所以∠OAE=∠DOF,所以∠DOF+∠AOE=∠OAE+ ∠AOE=90°,又易知E,O,F三点共线,所以∠AOD=90°,
考向2补形法——存在侧棱与底面垂直例2(2023·全国乙,文16)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA= .
[对点训练2](2024·湘豫名校第一次联考)已知三棱锥P-ABC中,PB⊥平面ABC,PB= ,AC=6,∠ABC=120°,则三棱锥P-ABC外接球的表面积为 .
解析 由题意,将三棱锥P-ABC补成直三棱柱TPS-ABC,则该直三棱柱的外接球即为三棱锥P-ABC的外接球,且直三棱柱的外接球球心落在上、下底面外接圆圆心连线的中点上.设△ABC外接圆的半径为r,三棱锥P-ABC外接球的半径为R.因为PB⊥平面ABC,AC=6,∠ABC=120°,由正弦定理,得
所以三棱锥P-ABC外接球的表面积为S=4πR2=60π.
考向3补形法——对棱相等例3(2024·河南开封模拟)已知四面体ABCD中,AB=CD
解析 设四面体ABCD的外接球的半径为R.因为四面体的对棱相等,所以可以把它补成一个长方体,把四面体的棱看作这个长方体的面对角线. 设这个长方体的长、宽、高分别为a,b,c,如图所示.
[对点训练3]已知棱长为1的正四面体的四个顶点都在一个球面上,则这个球的体积为( )
考向4截面法例4(2020·全国Ⅰ,理10)已知A,B,C为球O的球面上的三个点,☉O1为△ABC的外接圆.若☉O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )A.64πB.48πC.36πD.32π
解析 如图,在三棱锥P-ABC中,AB2+PA2=20=PB2,则PA⊥AB,同理PA⊥AC,而AB∩AC=A,AB,AC⊂平面ABC,因此PA⊥平面ABC.在等腰三角形ABC中,
因为OO1∥PA,取PA的中点D,连接OD,则有OD⊥PA,又O1A⊂平面ABC,即O1A⊥PA,从而O1A∥OD,四边形ODAO1为平行四边形,OO1=AD=1,又OO1⊥O1A,设球O的半径是R,则有R2=OA2=O1A2+O1O2
例5(1)(2024·浙江慈溪中学模拟)在三棱锥A-BCD中,AB⊥平面BCD, BC⊥CD,且AB=BC=CD=1,则其内切球的表面积为( )
解析 因为AB⊥平面BCD,所以AB⊥BD,AB⊥BC,AB⊥CD,又BC⊥CD,AB∩BC=B,所以CD⊥平面ABC,所以CD⊥AC.设三棱锥A-BCD的内切球的球心为O,半径为r,则VA-BCD=VO-ABC+VO-ABD+VO-ACD+VO-BCD=
(2)(2024·湖南郴州模拟)已知三棱锥P-ABC的棱长均为4,先在三棱锥P-ABC内放入一个内切球O1,然后再放入一个球O2,使得球O2与球O1及三棱锥P-ABC的三个侧面都相切,则球O2的表面积为 .
解析 如图所示,在三棱锥P-ABC中,取BC的中点D,连接AD,PD.过点P作PO垂直AD,点O是垂足.则两个球心O1,O2均在PO上,过点O1作O1N垂直PD,过点O2作O2E垂直PD,垂足分别为点N,E.依题意得S△ABC
解析 因为三棱锥A-BCD每组对棱棱长相等,所以可以把三棱锥A-BCD放入长方体中.设长方体的长、宽、高分别为x,y,z,如图所示.
考点三 与球切、接有关的最值问题
[对点训练6](2024·广东深圳模拟)如图,已知球的表面积为16π,若将该球放入一个圆锥内部,使球与圆锥底面和侧面都相切,则圆锥的体积的最小值为 .
适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练50球与几何体的切接问题课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练50球与几何体的切接问题课件新人教A版,共33页。PPT课件主要包含了ABD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第6章数列素能培优七破解基于问题情境的数列问题课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列素能培优七破解基于问题情境的数列问题课件新人教A版,共20页。PPT课件主要包含了ABD,ACD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第6章数列素能培优六数列中的构造问题课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列素能培优六数列中的构造问题课件新人教A版,共20页。PPT课件主要包含了规律方法,an2n-1+1,an4n-2n,an3n-1,ABD等内容,欢迎下载使用。












