江苏省盐城市滨海县+2023-2024学年九年级下学期3月月考数学试题

这是一份江苏省盐城市滨海县+2023-2024学年九年级下学期3月月考数学试题，共4页。

选择题
1．在2，0，1，9四个有理数中，没有倒数的数是
A．2B．0C．1D．9
2．下列图形中，既是轴对称图形又是中心对称图形的是
A．B．C．D．
3．若点M位于x轴的下方，y轴右侧，距x轴3个单位长，距y轴5个单位长，则M的坐标是
A．（﹣3，﹣5）B．（﹣3，5）C．（﹣5，﹣3）D．（5，﹣3）
4．盐城是生态绿色之城，有海洋、湿地、森林三大生态系统，拥有中国黄（渤）海候鸟栖息地世界自然遗产.其中湿地占地面积近770000公顷，被誉为“东方湿地之都”，并荣获“国际湿地城市”称号.数据770000用科学记数法表示为
A．7.7×104B．77×104C．0.77×105D．7.7×105
5．若关于的一元二次方程有两个相等的实数根，则实数的值为
A．B．C．D．9
6．先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源，如图是喜庆集会时
击鼓瞬间的情景及鼓的立体图形，该立体图形的主视图是
A． B．C． D．
7．如图，AB∥CD，∠ABE＝150°，∠BEF＝70°，则∠DFE的度数为
y
x
2
x＝-1
A．30°B．40°C．50° D．60°
第7题 第8题 第12题
8．函数y＝ax2+bx+c（a≠0）的部分图象如图所示，对称轴是直线x＝-1，与x轴的一个交点坐标为（2，0）．给出下列结论：①c＞a；②当y＞0时，x＞2；③3a+c<0；④若点A（x1，y1）、B（x2，y2）是图象上任意两点，且|x1+1|＜|x2+1|，则y1＜y2；⑤对于任意实数m，关于x的方程ax2+（b-m）x+c＝m有两个不相等的实数根．其中正确的结论有
A．5个 B．4个 C．3个 D．2个
填空题
9．如果有意义，那么的取值范围是 ▲ ．
10．若分式的值为1，则的值为 ▲ ．
11．因式分解：m2﹣4n2＝ ▲ ．
12．小明把如图所示的正八边形纸板挂在墙上玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等），则飞镖落在阴影区域的概率是 ▲ ．
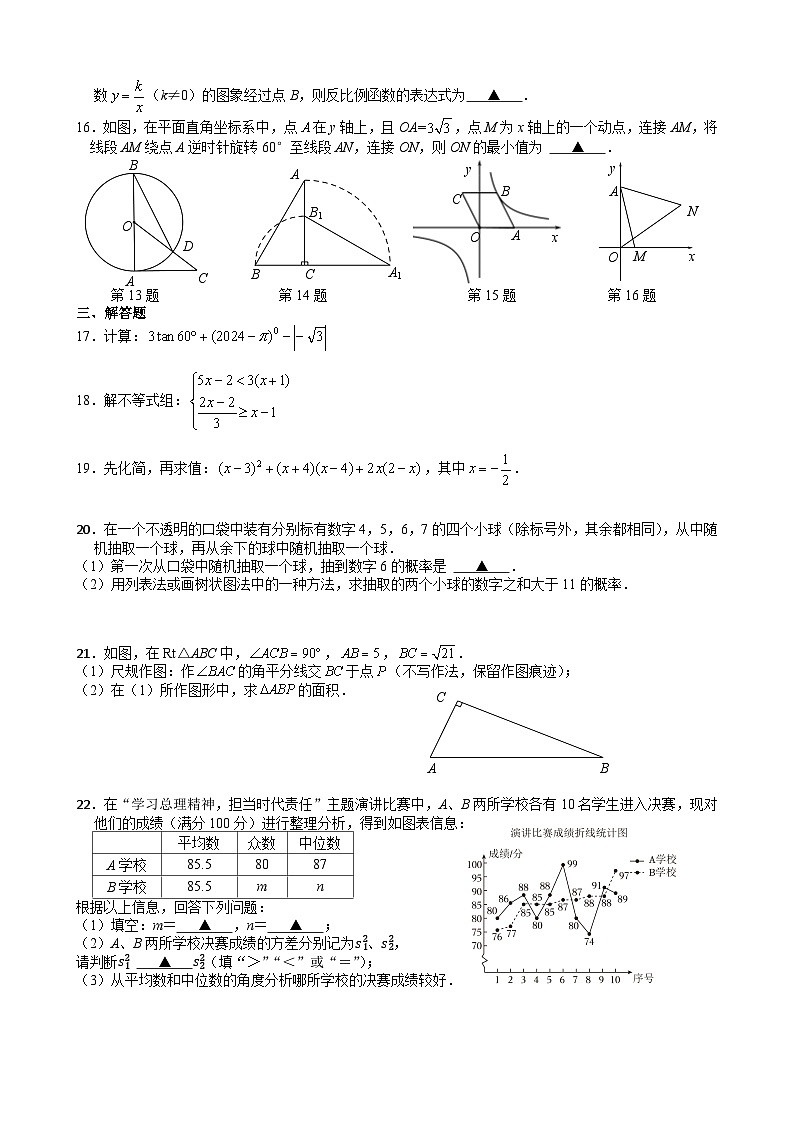
13．如图，已知是的直径，是的切线，连接交于点，连接．若∠C=38°，则的度数是 ▲ ．
14．如图，把一个含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C，已知BC＝2，则在旋转过程中点A经过的路径长为 ▲ ．
15．如图，在平面直角坐标系中，▱ABCO的顶点A、C的坐标分别为A（2，0）、C（﹣1，2），反比例函数（k≠0）的图象经过点B，则反比例函数的表达式为 ▲ ．
x
O
A
M
N
y
O
A
x
B
C
y
D
C
A
O
B
16．如图，在平面直角坐标系中，点在y轴上，且OA=，点M为x轴上的一个动点，连接AM，将线段AM绕点A逆时针旋转60°至线段AN，连接ON，则ON的最小值为 ▲ ．
B
C
A
B1
A1


第13题 第14题 第15题 第16题
三、解答题
17．计算：
解不等式组：
先化简，再求值：，其中．
在一个不透明的口袋中装有分别标有数字4，5，6，7的四个小球（除标号外，其余都相同），从中随机抽取一个球，再从余下的球中随机抽取一个球．
（1）第一次从口袋中随机抽取一个球，抽到数字6的概率是 ▲ ．
（2）用列表法或画树状图法中的一种方法，求抽取的两个小球的数字之和大于11的概率．
如图，在Rt△ABC中，，，．
（1）尺规作图：作的角平分线交于点（不写作法，保留作图痕迹）；
A
B
C
（2）在（1）所作图形中，求的面积．
在“学习总理精神，担当时代责任”主题演讲比赛中，A、B两所学校各有10名学生进入决赛，现对他们的成绩（满分100分）进行整理分析，得到如图表信息：
根据以上信息，回答下列问题：
（1）填空：m＝ ▲ ，n＝ ▲ ；
（2）A、B两所学校决赛成绩的方差分别记为s12、s22，
请判断s12 ▲ s22（填“＞”“＜”或“＝”）；
（3）从平均数和中位数的角度分析哪所学校的决赛成绩较好．
23．A
B
C
E
O
D
如图，四边形ABCD是⊙O的内接四边形，AB是直径，C是BD的中点，过点C作CE⊥AD交AD的延长线于点E．
（1）求证：CE是⊙O的切线；
（2）若BC＝6，AC＝8，求CE，DE的长．

24．定义：任意两个数a，b，按规则扩充得到一个新数c，称所得的新数c为“如意数”．
（1）若，，直接写出a，b的“如意数”c；
（2）如果，，求a，b的“如意数”c，并证明“如意数”；
（3）已知，且a，b的“如意数”，则b= ▲ （用含x的式子表示）.
25．如图1，某款线上教学设备由底座，支撑臂AB，连杆BC，悬臂CD和安装在D处的摄像头组成．如图2是该款设备放置在水平桌面上的示意图．已知支撑臂AB⊥l，AB＝18cm，BC＝40cm，CD＝44cm，固定∠ABC＝148°，可通过调试悬臂CD与连杆BC的夹角提高拍摄效果．
（1）当悬臂CD与桌面l平行时，∠BCD＝ ▲ °；
（2）问悬臂端点C到桌面l的距离约为多少？
（3）已知摄像头点D到桌面l的距离为30cm时拍摄效果较好，那么此时悬臂CD与连杆BC的夹角∠BCD的度数约为多少？（参考数据：sin58°≈0.85，cs58°≈0.53，tan58°≈1.60）



26．如图，直线与轴、轴分别交于、两点，抛物线经过、两点．
（1）求抛物线的表达式；
（2）点是抛物线在第二象限内的点，过点作轴的平行线与直线交于点，求的长的最大值；
（3）点是线段上的动点，点是抛物线在第一象限内的动点，连结交轴于点．是否存在点，使与相似，若存在，求出点的横坐标；若不存在，说明理由．
27．苏科版八年级下册数学教材第95页“探索探究”第22题如下：
如图，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′
的顶点A′与点O重合，将正方形，在这个过程中，这两个正方形重合部分
的面积会发生变化吗？证明你的结论．
【问题背景】
通过研究我们知道无论正方形A′B′C′D′绕点A′怎样转动，两个正方形重叠部分的面积，总等于一个正方形ABCD面积的．想一想，这是为什么？（此问题不需要作答）
九年级数学兴趣小组对上面的问题又进行了拓展探究、内容如下：正方形ABCD的对角线相交于点O，点P落在线段OC上，（k为常数）．
【特例证明】
（1）如图1，将Rt△PEF的直角顶点P与点O重合，两直角边分别与边AB，BC相交于点M，N．
①填空：k＝ ▲ ；
②求证：PM＝PN．（提示：借鉴解决【问题背景】的思路和方法，可直接证明△PAM≌△PBN；也可过点P分别作AB，BC的垂线构造全等三角形证明．请选择其中一种方法解答问题②．）
【类比探究】
（2）如图2，将图1中的△PEF沿OC方向平移，判断PM与PN的数量关系（用含k的式子表示），并说明理由．
【拓展运用】
（3）如图3，点N在边BC上，∠BPN＝45°，延长NP交边CD于点E，若EN＝kPN，则k= ▲ ．

平均数
众数
中位数
A学校
85.5
80
87
B学校
85.5
m
n