



所属成套资源:中考数学二轮复习考点提分特训专题(2份打包,原卷版+解析版)
中考数学二轮复习考点提分特训专题10 二次函数综合问题(2份打包,原卷版+解析版)
展开
这是一份中考数学二轮复习考点提分特训专题10 二次函数综合问题(2份打包,原卷版+解析版),文件包含中考数学二轮复习考点提分特训专题10二次函数综合问题原卷版doc、中考数学二轮复习考点提分特训专题10二次函数综合问题解析版doc等2份试卷配套教学资源,其中试卷共111页, 欢迎下载使用。
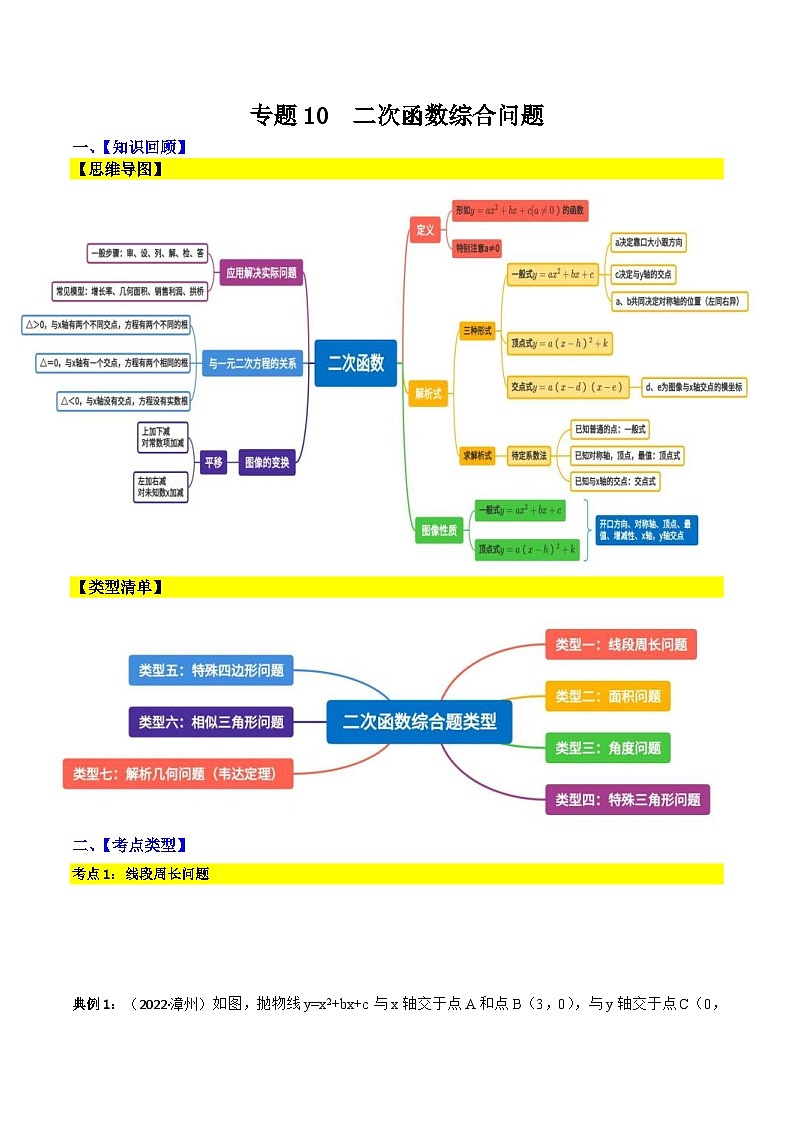
【思维导图】
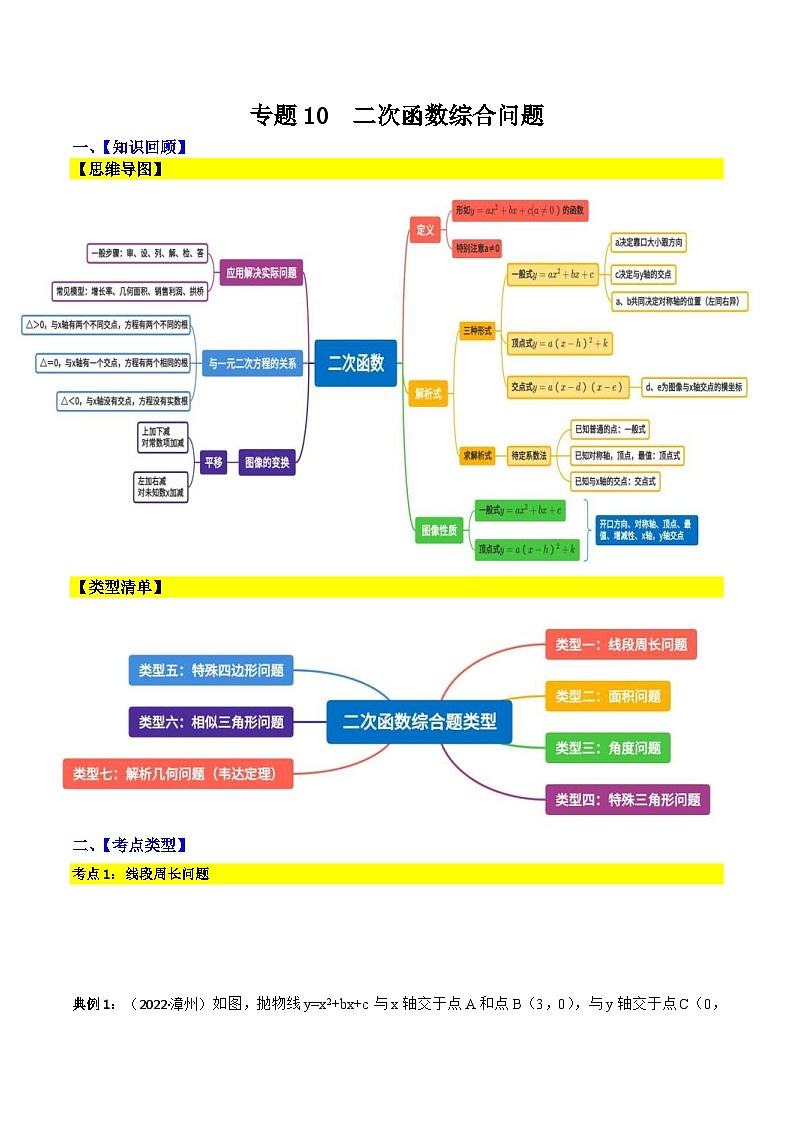
【类型清单】
二、【考点类型】
考点1:线段周长问题
典例1:(2022·漳州)如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【变式1】(2018·大庆)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)点D为抛物线对称轴上一点.
①当△BCD是以BC为直角边的直角三角形时,直接写出点D的坐标;
②若△BCD是锐角三角形,直接写出点D的纵坐标n的取值范围.
【变式2】(2022九上·东阳月考)如图,抛物线y=ax2+bx+c经过A(﹣1,0),B(3,0),C(0,3)三点,D为直线BC上方抛物线上一动点,过点D做DQ⊥x轴于点M,DQ与BC相交于点M.DE⊥BC于E.
(1)求抛物线的函数表达式;
(2)求线段DE长度的最大值;
(3)连接AC,是否存在点D,使得△CDE中有一个角与∠CAO相等?若存在,求点D的横坐标;若不存在,请说明理由.
【变式3】(2022九上·鄞州月考)如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点P,求△PAD周长的最小值;
(3)抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标.
考点2:面积问题
典例2:(2021九上·鄂城期末)如图1,在平面直角坐标系 中,抛物线 经过点 ,且与直线 在第二象限交于点A,过点A作 轴,垂足为点 .若P是直线 上方该抛物线上的一个动点,过点P作 轴于点C,交 于点D,连接 , .
(1)求抛物线的解析式;
(2)求 的面积S的最大值;
(3)连接 交 于点E,如图2,线段 与 能否互相平分?若能,请求出点E的坐标;若不能,请说明理由.
【变式1】(2022九上·岳麓开学考)如图,抛物线经过、两点,与轴交于点,点是抛物线上一动点,设点的横坐标为,连结、、、.
(1)求抛物线的函数表达式.
(2)当的面积等于的面积的时,求的值.
(3)当时,若点是轴上一动点,点是抛物线上一动点,试判断是否存在这样的点,使得以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的的坐标;若不存在,请说明理由.
【变式2】(2022九上·舟山月考)如图,抛物线经过点A(2,0),B(-2,4),(-4,0),直线AB与抛物线的对称轴交于点E.
(1)求抛物线的表达式;
(2)点M在直线AB上方的抛物线上运动,当ΔABM的面积最大时,求点M的坐标;
(3)若点F为平面内的一点,且以点为顶点的四边形是平行四边形,请写出符合条件的点F的坐标.
【变式3】(2021九上·槐荫期末)二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,过点P作PD⊥x轴于点D.
(1)求二次函数的表达式;
(2)连接PA,PC,求的最大值;
(3)连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.
考点3:角度问题
典例3:(2022九下·磐安期中)如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 .
(1)求抛物线的函数表达式;
(2)若点 在 轴上,在该抛物线的对称轴上,是否存在唯一的点 ,满足 ?如果存在,请求出点 的坐标;如果不存在,请说明理由;
(3)若点 在 轴上,满足 的点 是否存在?如果存在,请求出点 的坐标;如果不存在,请说明理由.
【变式1】(2021九上·潮安期末)如图,在平面直角坐标系中,抛物线过点,,与y轴交于点C,连接BC,点N是第一象限抛物线上一点,连接NA,交y轴于点E,.
(1)求抛物线的解析式;
(2)求线段AN的长;
(3)若点M在第三象限抛物线上,连接MN,,则这时点M的坐标为 (直接写出结果).
【变式2】(2022·通辽)如图,抛物线与轴交于,两点,与轴交于点,直线方程为.
(1)求抛物线的解析式;
(2)点为抛物线上一点,若,请直接写出点的坐标;
(3)点是抛物线上一点,若,求点的坐标.
【变式3】(2021九上·海珠期末)如图,已知直线y=﹣2x+m与抛物线相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)若点P是y轴上一点,当∠APB=90°时,求点P的坐标.
考点4:特殊三角形问题
典例4:(2022·湘西)定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).
(1)求抛物线C2的解析式和点G的坐标.
(2)点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN与线段DM的长度的比值.
(3)如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
【变式1】(2021九上·南充期末)如图,在平面直角坐标系中,抛物线的对称轴是直线 ,且与x轴交于A,B两点,与y轴交于点 , .
(1)求抛物线的解析式.
(2)在抛物线上是否存在点Q,使得 是以BC为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)设抛物线上的一点 的横坐标为m,且在直线BC的下方,求使 的面积为最大整数时点P的坐标.
【变式2】(2021九上·遂宁期末)如图,抛物线 与 轴交于 两点,与 轴交于点 ,直线 与抛物线交于 两点,与 轴交于点 ,且点 为 ;
(1)求抛物线及直线 的函数关系式;
(2)点 为抛物线顶点,在抛物线的对称轴上是否存点 ,使 为等腰三角形,若存在,求出点 的坐标;
(3)若点 是 轴上一点,且 ,请直接写出点 的坐标.
【变式3】(2022九上·温州月考)如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连结PA,PF,AF.
(1)求该抛物线所对应的函数表达式;
(2)如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
考点5:特殊四边形问题
典例5:(2022九下·重庆开学考)如图,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y= x-4.
(1)求抛物线的解析式;
(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;
(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.
【变式1】(2022九上·浦江期中)如图,在平面直角坐标系中,经过点A(4,0)的直线AB与y轴交于点B(0,4).经过原点O的抛物线y=﹣x2+bx+c交直线AB于点A,C,抛物线的顶点为D.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)M是线段AB上一点,N是抛物线上一点,当MN∥y轴且MN=2时,求点M的坐标;
(3)P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【变式2】21.(2022九上·海曙期中)如图, 拋物线交y轴于点,交x轴于点、C两点,点D为线段上的一个动点(不与重合),过点D作轴,交于点M,交抛物线于点N.
(1)求抛物线的解析式;
(2)连接和,当的面积最大时,求出点D的坐标及的最大面积;
(3)在平面内是否存在一点P,使得以点A,M,N,P为顶点,以为边的四边形是菱形?若存在,请求出点P的坐标;若不存在,请说明理由.
【变式3】(2022九上·义乌月考)如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1),且抛物线的对称轴与x轴的交点为Q.
(1)求该抛物线的函数表达式;
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,QA,QB,求四边形PAQB面积的最大值及此时P的坐标;
(3)将该抛物线向右平移2个单位长度得到抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点C,点D为原抛物线对称轴上的一点,在平面直角坐标系中是否存在点E,使以点B,C,D,E为顶点的四边形为菱形,若存在,请求出点E的坐标;若不存在,请说明理由.
考点6:相似三角形问题
典例6:(2022九上·镇海区开学考)如图,抛物线经过点、、三点.
(1)求此抛物线的解析式;
(2)P是抛物线上的一个动点,过作轴,垂足为,是否存在点,使得以、、为顶点的三角形与相似?若存在,请求出符合条件的点的坐标;若不存在,请说明理由;
(3)在直线上方的抛物线是有一点,使得的面积最大,求出点的坐标.
【变式1】(2022九下·长沙开学考)如图,在平面直角坐标系中,抛物线 与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.若线段 的长满足 ,则这样的抛物线称为“黄金”抛物线.如图,抛物线 为“黄金”抛物线,其与x轴交点为A,B(其中B在A的右侧),与y轴交于点C.且
(1)求抛物线的解析式;
(2)若P为 上方抛物线上的动点,过点P作 ,垂足为D.
①求 的最大值;
②连接 ,当 与 相似时,求点P的坐标.
【变式2】(2022九上·金东期末)已知抛物线与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,点P为抛物线上一动点(点P不与点C重合).
(1)当△ABC为直角三角形时,求△ABC的面积.
(2)如图,当APBC时,过点P作PQ⊥x轴于点Q,求BQ的长;
(3)当以点A,B,P为顶点的三角形和△ABC相似时(不包括两个三角形全等),求m的值.
【变式3】(2022九下·宁波月考)如图,已知抛物线y=-x2+bx+3的图象与x轴相交于点A和点B,与y轴交于点C,图象的对称轴为直线x=-1.连结AC,有一动点D在线段AC上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F.设点D的横坐标为m.
(1)求AB的长度;
(2)连结AE、CE,当△ACE的面积最大时,求点D的坐标:
(3)直接写出m为何值时,△ADF与△CDE相似.
考点7:解析几何问题(韦达定理)
典例7:(2022九上·杭州开学考)已知二次函数y=mx2﹣2mx+3,其中m≠0.
(1)若二次函数的图象经过(1,4),求二次函数表达式;
(2)若该二次函数图象开口向上,当﹣1≤x≤2时,二次函数图象的最高点为M,最低点为N,点M的纵坐标为6,求点M和点N的坐标;
(3)在二次函数图象上任取两点(x1,y1),(x2,y2),当a≤x1<x2≤a+2时,总有y1>y2,求a的取值范围.
【变式1】(2022九上·福建竞赛)已知开口向上的抛物线 与直线:y=ax+c,y=cx+a中的每一条都至多有一个公共点.
(1)求 的最大值;
(2)当 取最大值时,设直线 交抛物线 于A,B两点,C为抛物线的顶点,若△ABC内切圆的半径为1,求a的值.
【变式2】(2022九上·桐庐月考)已知二次函数y=ax2+bx+b﹣a(a≠0).
(1)若a=b时,求二次函数与x轴的交点坐标;
(2)若a>0,二次函数的对称轴为直线x=2,求该函数的最小值(用字母a表示);
(3)若该抛物线与直线y=ax+a(a≠0)交于A(x1,y1),B(x2,y2)两点,当x1<0<x2时,都有y1<y2,求证:b<2a.
【变式3】(2022九上·溪湖开学考)已知:抛物线:.
(1)若顶点坐标为,求和的值用含的代数式表示;
(2)当时,求函数的最大值;
(3)若不论为任何实数,直线与抛物线有且只有一个公共点,求,,的值;此时,若时,抛物线的最小值为,求的值.
相关试卷
这是一份中考数学二轮复习考点提分特训专题07 五大最值问题模型(2份打包,原卷版+解析版),文件包含中考数学二轮复习考点提分特训专题07五大最值问题模型原卷版doc、中考数学二轮复习考点提分特训专题07五大最值问题模型解析版doc等2份试卷配套教学资源,其中试卷共106页, 欢迎下载使用。
这是一份中考数学二轮复习考点提分特训专题06 五大常考相似模型(2份打包,原卷版+解析版),文件包含中考数学二轮复习考点提分特训专题06五大常考相似模型原卷版doc、中考数学二轮复习考点提分特训专题06五大常考相似模型解析版doc等2份试卷配套教学资源,其中试卷共102页, 欢迎下载使用。
这是一份中考数学二轮复习考点提分特训专题05 六大常考全等模型(2份打包,原卷版+解析版),文件包含中考数学二轮复习考点提分特训专题05六大常考全等模型原卷版doc、中考数学二轮复习考点提分特训专题05六大常考全等模型解析版doc等2份试卷配套教学资源,其中试卷共95页, 欢迎下载使用。









